
- •Векторное произведение векторов
- •Свойства векторного произведения
- •Смешанное произведение векторов
- •Плоскость.
- •Линии второго порядка
- •Исследование функций на экстремум. Выпуклость и вогнутость кривой, точки перегиба. Асимптоты
- •Исследование функций и построение их графиков
- •4.8. Поверхности второго порядка
- •Предел числовой последовательности. Предел функции
- •Бесконечно малые и бесконечно большие функции Сравнение бесконечно малых. Непрерывность функции. Точки разрыва и их классификация
- •Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически
- •Формула Тейлора и ее приложения
Исследование функций на экстремум. Выпуклость и вогнутость кривой, точки перегиба. Асимптоты
Если существует
окрестность
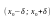 точки
точки
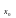 такая, что для всякой точки
такая, что для всякой точки
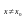 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство
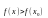 (или
(или
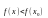 ),
то точка
называется точкой минимума (максимума)
функции
),
то точка
называется точкой минимума (максимума)
функции
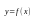 .
Точки минимума и максимума функции
называются ее точками экстремума.
.
Точки минимума и максимума функции
называются ее точками экстремума.
Теорема 1
(необходимое
условие экстремума). Если
– точка экстремума функции
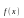 ,
то
,
то
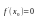 или
или
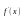 не существует (
– критическая точка этой функции).
не существует (
– критическая точка этой функции).
Теорема 2
(первое достаточное условие экстремума).
Пусть функция
дифференцируема в некоторой окрестности
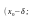
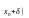 критической точки
,
за исключением, быть может, самой этой
точки. Если при этом в интервалах
критической точки
,
за исключением, быть может, самой этой
точки. Если при этом в интервалах
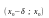 и
и
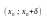 производная
имеет противоположные знаки, то
– точка
экст-ремума, причем если
производная
имеет противоположные знаки, то
– точка
экст-ремума, причем если
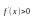 при
при
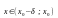 и
и
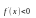 при
при
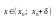 ,
то
– точка максимума. Если же
при
,
то
– точка максимума. Если же
при
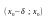 и
и
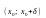 сохраняет знак, то точка
не является точкой экстремума.
сохраняет знак, то точка
не является точкой экстремума.
Теорема 3
(второе достаточное условие экстремума).
Пусть
дважды дифференцируема и
.
Если
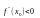 ,
то
– точка максимума функции
,
если
,
то
– точка максимума функции
,
если
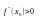 ,
то
– точка минимума. Если же
,
то
– точка минимума. Если же
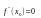 ,
то требуются дополнительные исследования.
,
то требуются дополнительные исследования.
Если на интервале (a; b) всякая касательная располагается выше (ниже) дуги кривой, то график дифференцируемой функции на этом интервале называется выпуклым (вогнутым).
Если
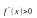 на интервале (a;
b), то график
функции является вогнутым на этом
интервале; если же
на интервале (a;
b), то график
функции является вогнутым на этом
интервале; если же
 ,
то график функции – выпуклый на (a;
b).
,
то график функции – выпуклый на (a;
b).
Точка
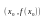 ,
при переходе через которую направление
вы-пуклости графика функции меняется
на противоположное, называется точкой
перегиба.
,
при переходе через которую направление
вы-пуклости графика функции меняется
на противоположное, называется точкой
перегиба.
Теорема 4
(необходимое условие точки перегиба).
Если
– абсцисса точки перегиба графика
функции
,
то
или
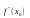 не существует.
не существует.
Теорема 5
(достаточное условие точки перегиба).
Пусть функция
дважды дифференцируема в некоторой
окрестности
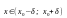 точки
,
в которой
или
не существует. Если при этом в интервалах
и
вторая производная
точки
,
в которой
или
не существует. Если при этом в интервалах
и
вторая производная
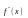 имеет противоположные знаки, то
имеет противоположные знаки, то
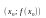 – точка перегиба.
– точка перегиба.
Прямая l называется асимптотой графика функции , если расстояние от точки М(x, f(x)) графика функции до прямой l стремится к нулю при неограниченном удалении точки М от начала координат.
Для существования
вертикальной асимптоты х
= а необходимо
и достаточно, чтобы хотя бы один из
односторонних пределов
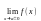 был равен бесконечности.
был равен бесконечности.
Для существования
наклонной асимптоты
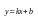 необходимо и достаточно существование
двух пределов
необходимо и достаточно существование
двух пределов
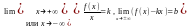 .
.
Исследование функций и построение их графиков
Исследование функций и построение их графиков удобно выпол-нять по следующей схеме.
Найти область определения функции.
Выяснить, является ли функция четной, нечетной, периодической.
Исследовать функцию на непрерывность, найти точки разрыва.
Найти асимптоты графика функции.
Установить интервалы монотонности функции. Найти точки экстремума функции, вычислить значения функции в этих точках.
Определить интервалы выпуклости и вогнутости графика функции, точки перегиба.
Используя результаты проведенного исследования, построить график функции. При необходимости уточнения отдельных участков кривой можно вычислить координаты нескольких дополнительных точек (в частности, координаты точек пересечения графика с осями координат).
