Вопрос 11. Взаимное расположение двух прямых на плоскости.
Взаимное расположение двух прямых на плоскости.
Теорема. Пусть
и 
– общие уравнения двух прямых на координатной плоскости Оху. Тогда
1)
если 
,
то прямые 
и 
совпадают;
2)
если 
,
то прямые
и
параллельные;
3)
если 
,
то прямые пересекаются.
Доказательство.
Условие 
равносильно
коллинеарности нормальных векторов данных
прямых:
.
Поэтому, если
,
то 
и прямые
пересекаются.
Если
же 
,
то 
, 
, 
и
уравнение прямой
принимает
вид:
или 
,
т.е. прямые совпадают.
Заметим, что коэффициент пропорциональности 
,
иначе все коэффициенты общего уравнения были
бы равны нулю, что невозможно.
Если же прямые не совпадают и не пересекаются, то остается случай , т.е. прямые параллельны.
Теорема доказана.
Заметим, что если прямые пересекаются, то для нахождения координат их точки пересечения достаточно решить систему двух уравнений с двумя неизвестными:
.
(4)
Следствие.
Пусть 
–
определитель системы (4).
Если 
,
то прямые пересекаются
в одной точке и система (4)
имеет единственное решение, которое
можно найти по формулам Крамера:
,
(5)
где 
, 
.
Если 
,
то прямые или
параллельны и тогда система (4)
не имеет решений, или прямые совпадают
и тогда система (4)
имеет бесконечно много решений.
Доказательство. По определению определителя второго порядка
.
Если
,
то 
и
,
т.е. прямые пересекаются
и координаты точки
пересечения можно найти по формулам
Крамера (5).
Если
же
,
то 
и 
,
т.е. либо прямые параллельны
и тогда система не
может иметь ни одного решения,
либо прямыесовпадают
и тогда система (4)
состоит из одного уравнения и
решениями такой системы являются координаты любой
точки, лежащей на прямой, а их бесконечно
много.
следствие доказано.
Пример. Выяснить взаимное расположение двух прямых
и 
и если они пересекаются, найти их точку пересечения.
Решение. Решим систему
.
Определитель системы
,
следовательно прямые пересекаются. Вычисляем координаты точки пересечения:
, 
,
, 
.
Ответ. Прямые пересекаются
в точке 
.
Вопрос
12.
Расстояние от точки до прямой на
плоскости
1. Нормальное
уравнение прямой
где p -
длина перпендикуляра (нормали), опущенного
из начала координат на прямую, а 
-
угол наклона этого перпендикуляра к
оси Ox.
Чтобы привести общее уравнение
прямой Ax + By + C =
0 к нормальному виду, нужно все члены
его умножить на нормирующий множитель 
,
взятый со знаком, противоположным знаку
свободного члена C.
2. Расстояние
точки A(x1, y1)
до прямой Ax + By + C =
0 есть длина перпендикуляра, опущенного
из этой точки на прямую. Она определяется
по формуле
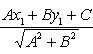
Правило. Чтобы
определить расстояние точки A(x1, y1)
до прямой Ax + By + C =
0, нужно привести уравнение прямой к
нормальному виду, взять левую часть
полученного уравнения и подставить в
нее вместо текущих координат координаты
данной точки. Абсолютная величина
полученного числа и даст искомое
расстояние:
Расстояние
от точки до прямой есть всегда величина
положительная. Кроме расстояния от
точки до прямой, рассматривается еще
так называемое отклонение точки от
прямой.
Отклонение 
данной
точки от данной прямой есть расстояние
от этой точки до прямой, которому
приписывается знак плюс, если точка и
начало координат находятся по разные
стороны от прямой, и знак минус, если
точка и начало координат находятся по
одну сторону от прямой.
Расстояние
от точки до прямой есть абсолютная
величина отклонения этой точки от
прямой.
Вопрос
13.
Различные способы задания плоскости в
пространстве.
Способы
задания плоскости
Общее
уравнение плоскости (рис.
4.13)
где 
-
нормальный вектор плоскости.
В
векторном виде 
,
Частные случаи общего уравнения плоскости:
1) By + Cz + D = 0 - параллельна оси Ox;
2) Ax + Cz + D = 0 - параллельна оси Oy;
3) Ax + By + D = 0 - параллельна оси Oz;
4) Cz + D = 0 - параллельна оси Oxy;
5) By + D = 0 - параллельна оси Oxz;
6) Ax + D = 0 - параллельна оси Oyz;
7) Ax + By + Cz = 0 - проходит через начало координат;
8) By + Cz = 0 - проходит через ось Ox;
9) Ax + Cz = 0 - проходит через ось Oy;
10) Ax + By = 0 - проходит через ось Oz;
11) z = 0 - плоскость Oxy;
12) y = 0 - плоскость Oxz;
13) x = 0 - плоскость Oyz.
Уравнение плоскости в отрезках
где a,
b, c -
величины отрезков, отсекаемых плоскостью
на осях координат.
Нормальное
уравнение плоскости
где 
-
углы, образуемые нормальным вектором
плоскости с осями координат; p -
расстояние от начала координат до
плоскости.
Приведение общего уравнения плоскости к нормальному виду:
Здесь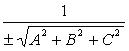 
-
нормирующий множитель плоскости, знак
которого выбирается противоположным
знаку D,
если 
произвольно,
если D =
0.
Уравнение
плоскости по точке и нормальному вектору
В векторном виде
В
координатах
Уравнение
плоскости по точке и двум неколлинеарным
векторам
В векторном виде
В координатах
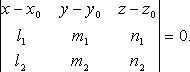
Уравнение плоскости по трем точкам
В векторном виде
В координатах
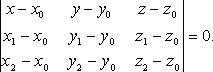
или
Параметрические
уравнения плоскости
В
векторном виде
В координатах
Уравнение
плоскости, проходящей через две
параллельные прямые
и 
Если прямые заданы соответственно уравнениям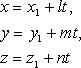и:
и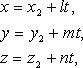 
то уравнение плоскости есть
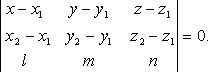
Уравнение
плоскости, проходящей через две
пересекающиеся прямые 
и 
или 
Если 
,
то уравнение плоскости есть
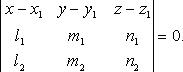Отклонение
точки от плоскости
или
где
знак перед
корнем
противоположен
знаку D,
если
и
выбран произвольно, если D
= 0.
Вопрос
14.Взаимное
расположение двух прямых в пространстве.
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями
