2.8. Численные методы анализа

Важнейшая область приложения программирования – инженерные расчеты. Здесь широко используются методы вычислительной математики. Рассмотрим некоторые из популярных численных методов.

Вычисление определенного интеграла. Аналитическое интегрирова­ние возможно лишь для небольшого класса “табличных” функций. В других случаях приходится прибегать к приближенным методам. Нахождение определенного интеграла заключается в вычислении площади под подинтегральной функцией в заданном диапазоне аргумента. Самый простой, но и самый грубый метод – метод прямоугольников (рис. 2.8.1).

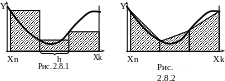
Здесь диапазон интегрирования от начальной точки Xn до конечной Xk разбивается на небольшие участки (всего N участков) с основанием h. Сумма площадей всех участков (Y(Xi)*h) и будет считаться интегралом.

Xk n–1

S =_Y(x)dX Y(X_i)*h

_Xn i=1

Приближенным значением интеграла S считаем сумму площадей всех прямоугольников под кривой (на рисунке заштрихованы). Видим, что погрешность метода весьма велика. Более точным является метод трапеций (рис. 2.8.2). Площадь элементарной трапеции (h[Y(Xi)+Y(Xi+h)]/2) гораздо лучше приближа­ется к кривой.

Программа (для функции Y=X²), реализующая оба метода, приведена ниже.

h=0.1: s=0 'задание шага h

Xn = 0: Xk = 5 'задание пределов интегрирования

FOR x = Xn TO Xk- h STEP h 'изменение текущих точек

's=s+h*x^2 'метод прямоугольников

s=s+h*(x^2+(x+h)^2)/2 'метод трапеций

NEXT

PRINT s

Отличие методов заключается лишь в одном операторе. Для метода прямоугольников он показан как комментарий.

Следует отметить, что при уменьшении шага интегрирования погрешность любого метода снижается, но поскольку метод трапеций более точен, здесь необходимая точность будет достигнута быстрее.

Определение действительных корней нелинейных алгебраических уравнений. Часто исследование математических моделей, например технологических процессов, приводит к необходимости решить то или иное алгебраическое уравнение, причем во многих случаях прямое аналитическое решение его затруднено или невозможно. Например, невозможно аналитически решить любое уравнение пятой степени. В связи с вышесказанным, были разработаны приближенные численные методы определения корней таких уравнений. Численное решение нелинейных алгебраических уравнений проводят в два этапа.

На ПЕРВОМ этапе необходимо отделить корни, т.е. найти такие интервалы изменения переменной, где расположен один корень.

Пусть задано уравнение: F(X,P1,P2, ... ,Pn) = 0.

Здесь: F – заданная функция,

X – неизвестная величина,

P1, P2, ..., Pn – коэффициенты.

Решить заданное уравнение – значит найти значения X (корни) ему удовлетворяющие. При любых других значениях F(X,P1,P2, ... ,Pn)#0.

Если заменить уравнение функцией Y=F(X,P1,P2,...Pn), а затем нарисовать ее график, то точки пересечения функцией оси Х и будут ее корнями. Признаком наличия корня на интересующем отрезке может служить противоположность знаков функции на его концах. Формальным признаком, удобным для программирования, является отрицательность произведения значений функции на концах отрезка.

На ВТОРОМ этапе определяют точное значение каждого корня.

Одним из самых простых методов такого определения является метод половинного деления. Суть метода иллюстрирует рис. 2.8.3 для функции Y=F(x). Положим, что определены границы интервала [a,b], внутри которого находится один корень функции Y=F(x). Исходный диапазон АВ делится пополам. Определяется тот из двух новых отрезков, на котором находится корень. На рисунке это отрезок АВ₁. Этот новый отрезок снова делим пополам, снова определяем участок, на котором находится корень (А₁В₁). Затем снова (А₂В₁) и т.д. до тех пор, пока очередной отрезок не станет <E. Тогда в качестве корня можем взять любую из, ограничивающих последний отрезок, точек, например А. Формальным признаком пересечения кривой оси Х и наличия на участке корня являются разные знаки функции на краях отрезка. Иными словами – отрицательность произведения значений Y в этих точках. Алгоритм решения изображен на рис. 2.8.4, а программа ниже.

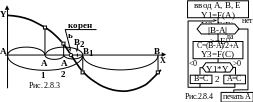
Программа нахождения корня методом половинного деления