Неск. Малі і великі функції

Функція н. м., якщо її границя =0.

Зауваження 1:

Для неск. малих функцій властива неск. кількість елементів.

Зауваження 2:

Якщо функція має границю в т. а, тоді в деякому околі цієї точки f(x)=A+a(x).

Неск малі функції:

1) с<>0, функції мають один порядок.

2) 0 тоді а(х)-неск мала вищого порядку.

3) 1 – еквівалентні

4) 1 –непорівнені

Неперервність функції в точці

якщо 

Коші:

Гейне:

{x_n}a {f(x_n)A}

Теорема:

Означ. за Гейне і Коші еквівалентні.

Означення:

Функція неперервна зправа (зліва)

Неперервність скл. Функції

Функція утворена накладанням двох,або декількох функцій називається складеною.

Нехай x=(t) неперервна в т. t₀,

а f(x) в т. х_0. x₀=(x₀), тоді

f((t)) неперервна в т. t₀,то

Неперервність елементарних функцій

Найпростіші функції є неперервними в областях де вони визначенні.

Доведення:

Елементарними функціями наз. функції одержані за допомогою арифм. опер. та суперпозиції над найпростішими функціями.

Якщо елементарна функція визначена в околі якоїсь точки, то вона неперервна в ції точці.

3,4,5 Границі(наслідки із 2)

3)

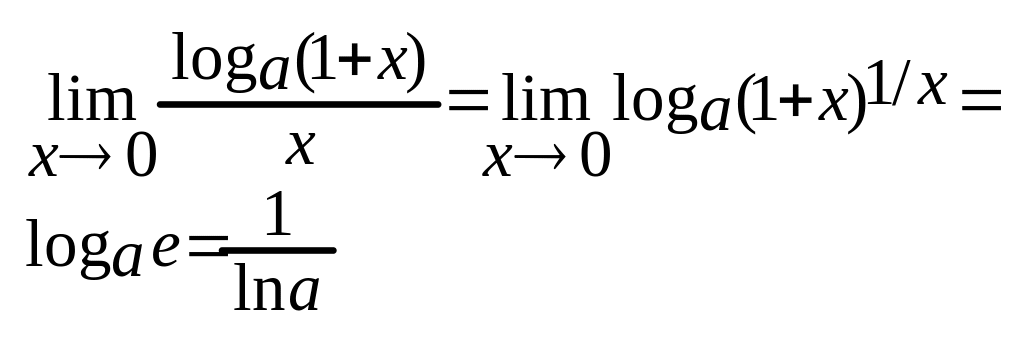
4)

5)

(1+x)^m-1=y => (1+x)^m=y+1 =>

mln(1+x)=ln(1+y) =>

Границя степенево-показникової функції

y=U(x)^V(x) в т. х₀- ф. непер. U(x)>0

1) Якщо

U₀>0

y=U^V=e^VlnU

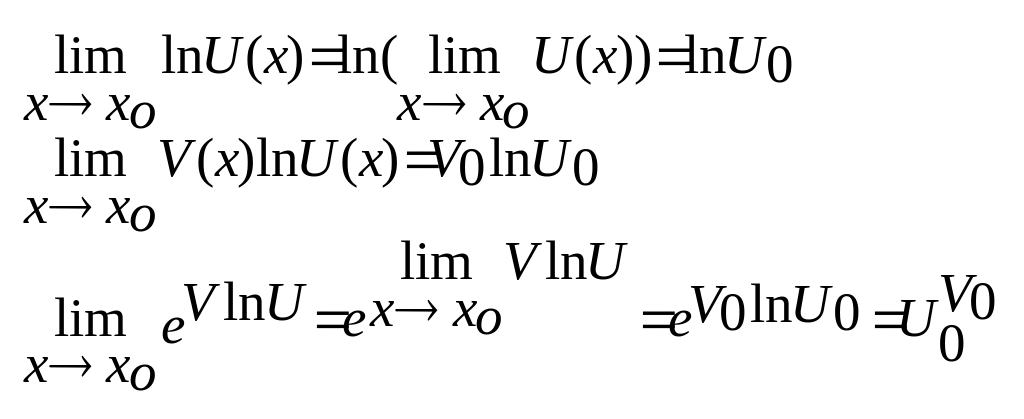2) Якщо умови не виконані

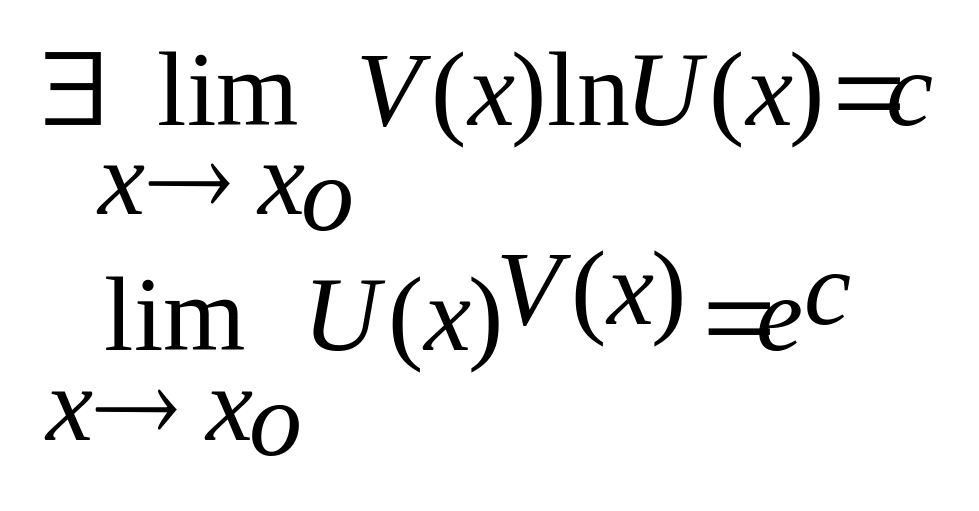
3)

1.

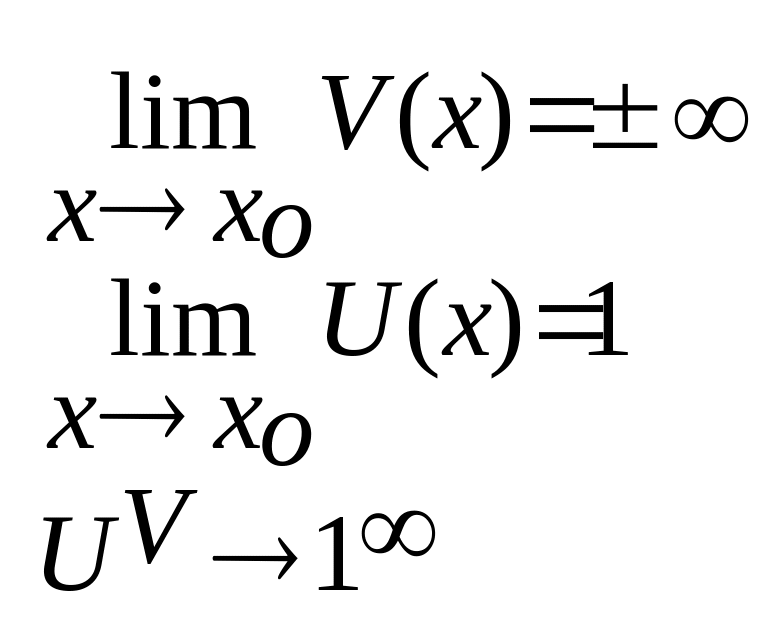
2.

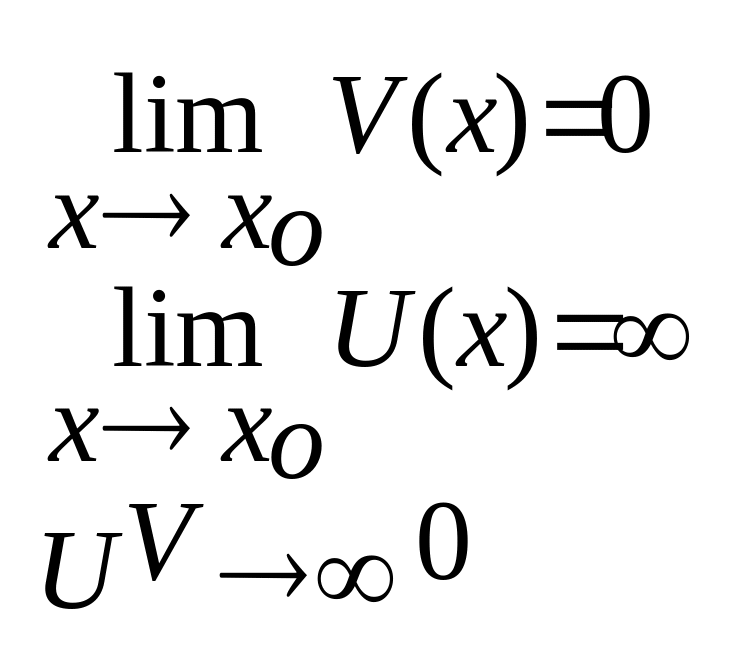
3.

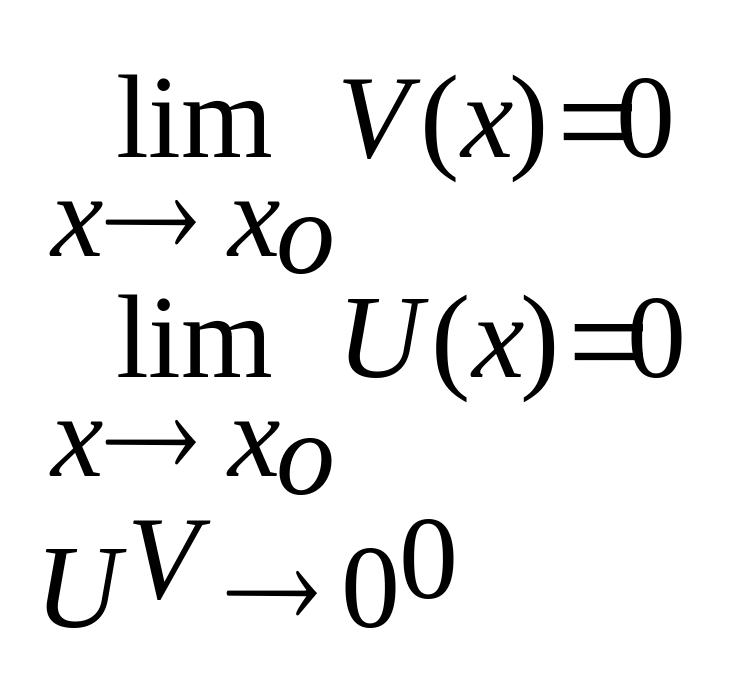
якщо () => 0/0

якщо 1^,0⁰,⁰, то

U^V=e^VlnU

Точки розриву

1. Перщого роду:

1) Усувною точкою розриву називають точку х₀, якщо

 f(х)

якщо замінити f(x) на , то отримаєм непер. ф.

2) Неусувна точка:

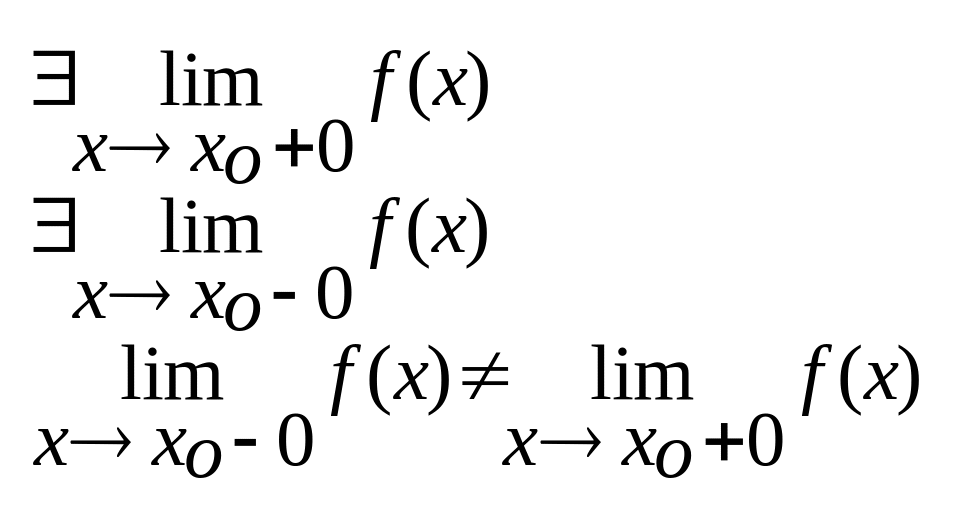
2.Другого роду:

Якщо хоча б одна з одностор. гр. не існує або неск. велика.

1 Теорема Больцано – Коші

Функція неперервна на [a,b] і на кінцях приймає значення різних знаків, тоді існує т. с є [a,b], що f(0)=0

Доведення.

Розіб’ємо [a,b] навпіл в середині знайдемо f(x)=0,якщо f(x)<>0 тоді візьмемо ту половину на якій функція приймає знач. різних знаків.(b-a)/n якщо b-a та n прямує до безкінечності. Система вкладених сегментів збіжна, тоді існує 1 точка С , яка належить всім відрізкам. Доведемо, що С=0, припустимо, що С<>0

Точка С є[a,b],т.к функція неперервна на [a,b],то вона неперервна в т. С , в якій вона не рівна 0. За теорією постійності знаку існує деякий окіл С, в якій ф. не міняє знак, але при дуже великих n окіл попадає в [a_n,b_n] на кінцях якого функція приймає різні знаки. Протиріччя. Доведено.

2 Теорема Больцано-Коші

Якщо функція неперервна на [a,b] та f(a)=A, f(b)=B, а С деяке число між А та В, то знайдеться точка с є[a,b], що f(c)=C.

Доведення.

Нехай A<C<B, Введемо функцію , вона неперервна, різниця непер. , і на кінцях [a,b] => приймає на кінцях [a,b] різні знаки, тобто для неї виконується 1 теорема => існує т. с є [a,b], , але => .

1-а Теорема Вейєрштрасса

Якщо функція неперервна на сегменті, то вона обмежена на ньому.

Доведення

1. f(x)- обмеж. зверху.

Припустимо супротивне:

M x[a,b]:f(x)>M

nN x_n[a,b]:f(x_n)>n

{x_n}-обмежена

{f(x_n)}-необмежена(неск.вел.)

за теор. Больцано-Веєрштрасса із {x_n} можна виділити збіжну підпосл. x_nkx_0(k) x₀[a,b]

оскільки f(x) неперервна на сегменті, то

але (запереч.)

1. f(x)- обмеж. знизу (аналогічно)

2-а Теорема Вейєрштрасса

Якщо функція неперервна на сегменті, то вона досягає свої точних границь.

Доведення:

1. Покажемо, що f(x) досягає sup.

Припустимо супротивне:

f(x) – неперервна (і обмеж. з 1-ї т. Вейєрштрасса), але не досягає sup

введем на [a,b]

 A>0 x[a,b]:(x)A =>

1/(M-f(x))A => (1/A)M-f(x) =>

f(x)(M-1/A)<M

2. Аналогічно inf.