38. Понятия дифференциального уравнения и его решения. Порядок дифференциального уравнения. Общее, особое, частное решения.

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.

Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.

Простейшим дифференциальным уравнением является уравнение вида Чтобы его решить, нужно представить производную как домножить обе части уравнения на dx и проинтегрировать обе части получившегося уравнения:

Как видно, это уравнение имеет бесконечное количество решений, отличающихся друг от друга на постоянную C . Выбрать конкретное решение уравнения можно, если знать начальные условия, например, точку, через которую проходит график функции y  =  y  ( x ). Так, если известно, что y  ( x ₀ ) =  y ₀, то подставляя это значение в общее решение получаем  откуда и . Это решение можно записать в виде .

Общим решением дифференциального уравнения называется функция y  =  y  ( x ,  C ₁,  C ₂,…,  C _n ), зависящая от n констант, если она является решением дифференциального уравнения при любых значениях постоянных C ₁, C ₂,…, C _n .

Частным решением дифференциального уравнения называется решение, получаемое из общего решения путем придания определенного значения постоянным C _i .

Наряду с частными существуют особые решения , которые нельзя получить из общего решения никакой подстановкой постоянных.

39. Задача Коши для уравнения первого порядка. Теорема существования и единственности. (Формулировка).

Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка

или

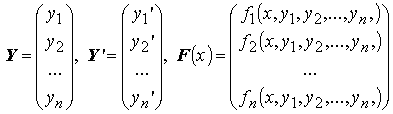
Задачей Коши для для этой системы называется следующая задача: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x₀)=Y₀, где Y₀ — некоторый постоянный вектор.

Справедлива следующая теорема о существовании и единственности решения задачи Коши.

Теорема Коши. Пусть в области D из Rⁿ⁺¹ непрерывны все компоненты вектора правой части F(x,Y) и их частные производные по Y:

Тогда, какова бы ни была начальная точка (x₀,Y₀) ≡ (x₀,y_{1, 0} ,y_{2, 0}, … ,y_{n, 0} ) ∈ D , существует такой отрезок [x₀ − h; x₀ + h] , что задача Коши   Y' = F(x,Y), что Y(x₀)=Y₀ имеет единственное решение.

Важно понимать, что теорема Коши имеет локальный характер: существование решения Y = Y(x) гарантируется лишь в достаточно малой окрестности точки x₀ , ( h > 0 может оказаться достаточно малым).

Важно также понимать, что теорема содержит только достаточные условия существования и единственности решения — при нарушении условий теоремы задача Коши может иметь или не иметь решений, может иметь несколько решений.

41. Линейные однородные уравнения с постоянными коэффициентами. Характеристическое уравнение. Метод Эйлера. Представление общего решения.

Решение дифференциального уравнения вида  или, короче,  будем искать в виде , где k = const.

  Т.к.   то

 При этом многочлен  называется характеристическим многочленом дифференциального уравнения.

  Для того, чтобы функция  являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы

 т.е.

  Т.к. e^kx ¹ 0, то  - это уравнение называется характеристическим уравнением. 

  Как и любое алгебраическое уравнение степени n, характеристическое уравнение  имеет n корней. Каждому корню характеристического уравнения k_i соответствует решение дифференциального уравнения.

  В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные.

Метод Эйлера. Рассмотрим дифференциальное уравнение           (1)с начальным условием Подставив в уравнение (1), получим значение производной в точке :

При малом  имеет место:

Обозначив  , перепишем последнее равенство в виде:          (2)

Принимая теперь за новую исходную точку, точно также получим:

В общем случае будем иметь:       (3)

Это и есть метод Эйлера. Величина  называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у , так как производная  на самом деле не остается постоянной на промежутке длиной . Поэтому мы получаем ошибку в определении значения функции у , тем большую, чем больше . Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.

??? Вид общего решения линейного однородного дифференциального уравнения для вещественных, комплексных и кратных корней характеристического уравнения.

Фундаментальная система решений и общее решение для случая простых действительных корней

Рассмотрим уравнение  y'' - 3y' + 2y = 0. Его характеристическое уравнение  l² - 3l + 2 = 0 имеет два различных действительных корня  l₁ =1 и l₂ =2. Фундаментальная система решений уравнения: y₁ = exp(l₁x)=exp(x) и y₂ = exp(l₂x)=exp(2x) Общее решение уравнения: y(x) = c₁exp(x) + c₂exp(2x).

Фундаментальная система решений и общее решение для случая простых комплексных корней

Рассмотрим уравнение y'' - 2y' + 5y = 0. Его характеристическое уравнение  l² - 2l + 5 = 0 имеет пару комплексно сопряженных корней  l₁ = 1-2i, l₂ = 1+ 2i. Фундаментальная система решений уравнения: exp(x)cos2x, exp(x)sin2x. Общее решение уравнения: y(x) = c₁exp(x)cos2x + c₂exp(x)sin2x.

Фундаментальная система решений и общее решение для случая кратных действительных корней

Рассмотрим уравнение y''- 2y' + y = 0. Его характеристическое уравнение l² - 2l + 1 = 0 имеет один кратный действительный корень l₁ = l₂ = 1. Фундаментальная система решений уравнения:  y₁ = exp(x) и y₂= xexp(x) Общее решение уравнения: y(x) = c₁exp(x) + c₂xexp(x).