
- •Механическая система
- •1. Виды механического движения ?
- •Элементарная формула
- •Вид преобразований при коллинеарных осях[4]
- •[Править] Формула преобразования скоростей
- •Классификация сил
- •1. По природе силы:
- •2. По работе, совершаемой силой:
- •Нелинейные деформации
- •[Править] Первый закон Кеплера (закон эллипсов)
- •[Править] Второй закон Кеплера (закон площадей)
- •[Править] Третий закон Кеплера (гармонический закон)
- •Вращающиеся системы отсчета
1. Виды механического движения ?
Механическое движение можно рассматривать для разных механических объектов:
Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
Криволинейное движение - это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Заметим, что при этом оно не обязательно является прямолинейным.
Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела положением любых двух точек.
Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).
2.
Координатная и векторная формы задания положения материальной точки в пространстве. Рассмотренное нами движение вдоль прямой линии является частным случаем движения в реальном трехмерном пространстве. Найдем его объективные характеристики, выявив сначала особенности собственно пространственных отношений при t = const, а затем перейдем к описанию в мире событий. Пример трехмерной ПСО приведен на рис. 2.3. В качестве системы координат выбрана декартова СК (положение точки задается тремя проекциями на оси x, y, z). На практике используют также полярные и сферические координаты. В сферических координатах положение точки задается с помощью двух углов o, , отмеченных на рис. 2.3, и радиус-вектора r). К реальному пространству с высокой степенью точности применима геометрия Евклида, которая наиболее просто выглядит в декартовой системе координат. Положение частицы А в момент времени t задается ее тремя пространственными координатами: x, y, z. Положение частицы А можно также характеризовать вектором расстояния r = OA = {x, y, z}, проведенным из начала отсчета в точку расположения частицы (см. рис. 2.3). Длина этого вектора равна:
|
|
|||||||||
|
Объективные характеристики пространства. Рассмотрим теперь две произвольно расположенные частицы A и B. Расстояние между ними r находится по теореме Пифагора:
Направление от одной частицы к другой задается через направляющие косинусы (косинусы углов между направлениями вектора r и соответствующей осью): cos 1 = x/r; cos 2 = y/r; cos 3 = z/r. (2.3) Рассмотрим, как влияет на величину разности проекций частиц выбор начала координат СО (см. рис. 2.4). Исходя из рис. 2.4 видно, что: инвариантными величинами являются разности координат, расстояние и направляющие косинусы, что в конечном итоге отражает такое свойство пространства как однородность. Рассмотрим, как влияет на величину разности проекций частицы ориентация осей координат (см. рис. 2.5). Из геометрических соображений и простых тригонометрических преобразований следует, что: x' = x·cos y·sin y' = x·cos y·sin z' = z; r' = r. (2.4) Таким образом, инвариантом, по-прежнему, является расстояние, в то время как разность проекций частиц на оси координат не являются таковыми. r = AB = {x, y, z}, (2.5) где x, y, z - проекции вектора r, проведенного от частицы A к частице B. Инвариантность величины r по отношению к повороту осей координат отражает такое свойство пространства как изотропность, заключающееся в независимости длины отрезков от их ориентации относительно осей координат. Что касается направления r, то его удобно связать с вектором er, модуль которого равен 1 (единичный вектор): er = r/r = {cos 1; cos 2; cos 3}. (2.6) Тогда вектор перемещения можно выразить как произведение его модуля на единичный вектор r = r·er. (2.7)
|
|||||||||
|
Скалярные и векторные величины в физике. Чтобы величина могла быть описана вектором, то для нее так же, как и для вектора расстояния должны выполняться следующие операции:
Совокупность численных значений величин f(x, y, z) в некоторой области пространства в данный момент времени называется скалярным полем. Например: поле температур, давлений и т.п. Совокупность численных значений величин и направлений вектора A(r) в некоторой области пространства в данный момент времени называется векторным полем. Например: поле скоростей, поле напряженности электрического поля и т.п. Физические законы, записанные в форме скаляров и векторов, являются инвариантными по отношению к выбору начала отсчета и поворота осей СО. Поэтому физические законы, выраженные через скалярные и векторные величины и их комбинации, могут быть равноправны по отношению к выбору СО, являясь т.о. объективными.
|
|||||||||
|
Координатный и векторный способы задания движения в пространстве. Пусть скалярные f и векторные величины A зависят от времени: f = f(t), A = A(t). Поведение скалярной величины задается обычной аналитической зависимостью f(t). В случае векторов дело обстоит несколько сложнее. Существуют два способа выражения зависимости A = A(t):
Координатный способ. Введем характеристики для координатного способа описания движения. Очевидно, что все три направления вдоль осей OX, OY, OZ равноправны. Таким образом для материальной точки, перемещающейся в 3 мерном пространстве, число степеней свободы (число независимых координат, определяющих положение тела в пространстве) равно трем. Ввиду равноправности трех взаимно перпендикулярных направлений (что является отражением такого свойства пространства как изотропность) движение частицы вдоль каждого из них можно описывать с помощью введенных ранее характеристик - проекций мгновенной скорости и ускорения на соответствующие оси координат. Только таких проекций будет три, а не одна, как в случае одномерного движения. r(t) = x(t)·i + y(t)·j + z(t)·k, (2.8) где i, j, k - единичные вектора, направленные вдоль осей координат. i = {1,0,0}; j = {0,1,0}; k = {0,0,1}. Вектора скорости и ускорения можно также выразить через их проекции и единичные вектора i, j, k: v = vx·i + vy·j + vz·k; a = ax·i + ay·j + az·k. (2.9) Следовательно, описать движение координатным способом, т.е. найти зависимости x(t), y(t), z(t), можно предварительно определив зависимости соответствующих проекций скорости от времени x(t), y(t), z(t).
|
|||||||||
|
Векторный способ заключается в нахождении зависимости r(t) = r(t)·er(t), т.е. задании величины и направления вектора r в любой момент времени. В случае плоского (двумерного) движения направление обычно задается в виде значения тангенса угла между вектором r и осью OX. Для векторного способа описания движения важным является понятие вектора перемещения r, равного приращению вектора r за время t: r = r(t + t) - r(t) = {x, y, z}. (2.10) Непрерывная линия, по которой перемещается частица в пространстве называется траекторией. Движение по траектории может происходить в любом направлении в отличии от перемещения частицы вдоль мировой линии. Уравнения траекторий в плоскостях XY, XZ, YZ можно получить путем исключения времени из графиков движения вдоль осей координат x(t), y(t), z(t). По аналогии с координатным способом описания движения введем понятия векторов мгновенной скорости и ускорения: (t) = lim r/t = dr/dt = r(t)·er(t). (2.11) a(t) = lim /t = (t)·e(t). (2.12) В векторном способе описания движения вектора и a задаются значениями их модулей и указанием направлений. Вектор r можно найти, исходя из векторного уравнения:
Заметим, что одно векторное уравнение заменяет три скалярных. Путь, пройденный частицей за конечный промежуток времени, задается выражением:
Путь - это скалярная величина, неравная модулю вектора перемещения (их равенство наблюдается только в случае прямолинейного движения частицы в одном направлении). |
|||||||||
|
Заметим, что вектора dr, а, следовательно, и всегда направлены по касательной к траектории. Ускорение параллельно вектору d. Следовательно, по отношению к вектору скорости вектор ускорения может быть сориентирован под произвольным углом. Поскольку в обоих способах описания движения мы исследовали одно явление, а характеристики, описывающие его, связаны между собой вполне определенными уравнениями (2.2, 2.3, 2.6 и 2.7), то координатный и векторный способы описания движения эквивалентны. |
|||||||||
Радиус-вектор
— Вектор, определяющий положение М. Т.
в пространстве:
![]() .
Здесь r1,r2,...,rn
— координаты
радиус-вектора. Геометрически изображается
вектором, проведенным из начала координат
к материальной точке. Зависимость
радиус-вектора (или его координат ri
= ri(t)) от времени
.
Здесь r1,r2,...,rn
— координаты
радиус-вектора. Геометрически изображается
вектором, проведенным из начала координат
к материальной точке. Зависимость
радиус-вектора (или его координат ri
= ri(t)) от времени
![]() называется
законом
движения.
называется
законом
движения.
Траектория — Годограф радиус-вектора, то есть — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется М. Т. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путем и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:
![]() ,
,
Где :
![]() —
модуль начальной скорости, а aS
= aτ — Тангенциальное ускорение.
—
модуль начальной скорости, а aS
= aτ — Тангенциальное ускорение.
Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:
![]() .
.
Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.
Путь в физике — длина участка траектории материальной точки.
Ускоре́ние — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Ско́рость (часто обозначается
![]() ,
от англ.
velocity или фр.
vitesse) — векторная
физическая
величина, характеризующая быстроту
перемещения
и направление движения материальной
точки в пространстве относительно
выбранной системы
отсчёта (например, угловая
скорость). Этим же словом может
называться скалярная
величина, точнее модуль
производной
радиус-вектора.
,
от англ.
velocity или фр.
vitesse) — векторная
физическая
величина, характеризующая быстроту
перемещения
и направление движения материальной
точки в пространстве относительно
выбранной системы
отсчёта (например, угловая
скорость). Этим же словом может
называться скалярная
величина, точнее модуль
производной
радиус-вектора.
3. Тангенциа́льное ускоре́ние —
компонента
ускорения,
направленная по касательной
к траектории
движения. Совпадает с направлением
вектора скорости при ускоренном движении
и противоположно направлено при
замедленном. Характеризует изменение
модуля
скорости. Обозначается обычно
![]() или
или
![]() (
(![]() ,
,![]() итд в соответствии с тем, какая буква
выбрана для обозначения ускорения
вообще в данном тексте). Величину
тангенциального ускорения - в смысле
проекции вектора ускорения на единичный
касательный вектор траектории - можно
выразить так:
итд в соответствии с тем, какая буква
выбрана для обозначения ускорения
вообще в данном тексте). Величину
тангенциального ускорения - в смысле
проекции вектора ускорения на единичный
касательный вектор траектории - можно
выразить так:
![]()
где
![]() -
путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент
-
путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент
Центростремительное (нормальное) ускорение — часть полного ускорения точки, обусловленного кривизной траектории и скоростью движения по ней материальной точки. Такое ускорение направлено к центру кривизны траектории, чем и обусловлен термин. Формально и по существу термин центростремительное ускорение в целом совпадает с термином нормальное ускорение, различаясь скорее лишь стилистически (иногда исторически)[1].

 К
определению вектора перемещения.
К
определению вектора перемещения.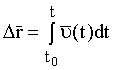 .
(2.13)
.
(2.13) .
(2.14)
.
(2.14)