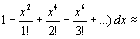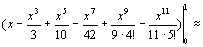- •1. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами.
- •2. Ряды с положительными членами. Признаки сходимости.
- •4. Знакочередующиеся ряды. Теорема Лейбница.
- •5. Функциональные ряды. Область сходимости
- •6. Равномерная сходимость. Свойства равномерно сходящихся рядов
- •2. Свойства равномерно сходящихся рядов.
- •7. Степенные ряды. Теорема Абеля. Радиус сходимости.
- •8. Свойства степенных рядов. Ряды Тейлора и Маклорена.
- •12. Примеры функциональных пространств
7. Степенные ряды. Теорема Абеля. Радиус сходимости.
Определение 1.1. Степенным рядом называется функциональный ряд вида
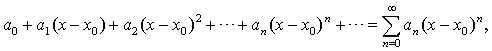 (1.1) где a0, a1, a2,
…,an,…, а также x0 – постоянные
числа. Точку x0 называют центром
степенного ряда.
(1.1) где a0, a1, a2,
…,an,…, а также x0 – постоянные
числа. Точку x0 называют центром
степенного ряда.
Теорема
Абеля. Если
степенной ряд (1.2) сходится при некотором ![]() ,
где
,
где![]() -число,
не равное нулю, то он сходится абсолютно
при всех значениях x таких,
что
-число,
не равное нулю, то он сходится абсолютно
при всех значениях x таких,
что ![]() Наоборот,
если ряд (12) расходится при
,
то он расходится при всех значениях x таких,
что
Наоборот,
если ряд (12) расходится при
,
то он расходится при всех значениях x таких,
что ![]()
Доказательство. Пусть числовой ряд
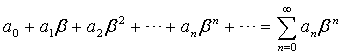 (1.3) сходится.
Поэтому
(1.3) сходится.
Поэтому ![]() Но
любая последовательность, имеющая
предел, ограничена, значит, существует
такое число M, что
Но
любая последовательность, имеющая
предел, ограничена, значит, существует
такое число M, что ![]() для
всех n=0,1,2,…
для
всех n=0,1,2,…
Рассмотрим теперь ряд
![]() (1.4)
(1.4)
предполагая,
что ![]() Так
как
Так
как 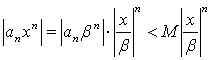 и
при этом
и
при этом ![]() то
члены ряда (3.4) не превосходят соответствующих
членов сходящегося ряда
то
члены ряда (3.4) не превосходят соответствующих
членов сходящегося ряда
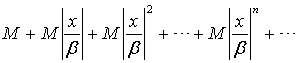
(геометрической прогрессии). Следовательно, ряд (1.4) сходится, а ряд (1.2) абсолютно сходится.
Предположим теперь, что ряд (1.3) расходится, а ряд (1.2) сходится при Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.
Теорема 1.2. Для степенного ряда (1.2) возможны только три случая:
1) ряд сходится в единственной точке x=0;
2) ряд сходится при всех значениях x;
3) существует
такое R>0, что ряд сходится при всех
значениях x, для которых ![]() и
расходится при всех x, для которых
и
расходится при всех x, для которых ![]()
Определение 1.2. Интервал (-R,R), где число R определено в теореме 1.2, называется интервалом сходимости ряда (1.2), а число R – радиусом сходимости этого ряда.
Теорема о радиусе сходимости.
Для
каждого степенного ряда  существует
существует ![]() ,
удовлетворяющее свойствам:
,
удовлетворяющее свойствам:
Если
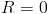 ,
то ряд сходится только при
,
то ряд сходится только при 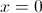 .
.Если
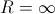 ,
то ряд сходится при любых
,
то ряд сходится при любых 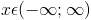 .
.Если
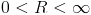 ,
то ряд сходится при
,
то ряд сходится при 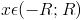 и
расходится при
и
расходится при 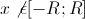 .
.
Сходимость
на любом отрезке внутри интервала![]() равномерная.
равномерная.
Число ![]() - радиус
сходимости степенного ряда.
- радиус
сходимости степенного ряда.
Формулы для радиуса сходимости степенного ряда.
1.
Если существует (конечный или бесконечный)
предел ![]() ,
то радиус сходимости степенного
ряда
вычисляется
по формуле:
,
то радиус сходимости степенного
ряда
вычисляется
по формуле:
![]()
2.
Если существует (конечный или бесконечный)
предел ![]() ,
то:
,
то:
![]()
Замечание.
Ряд 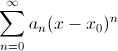 с
центром
с
центром ![]() сводится
к
сводится
к 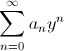 заменой
заменой ![]() .
.
Все наши результаты переносятся на общие степенные ряды.
В
частности, ряд сходится на ![]() и
расходится вне соответствующего отрезка.
и
расходится вне соответствующего отрезка.
Теорема
4:
Если ряд
имеет
радиус сходимости
,
то такой же радиус сходимости имеют
ряды 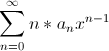 и
и  .
.
Итак, если формально проинтегрировать или продифференцировать ряд , то радиус сходимости не изменится.
Пример
10. Найти область сходимости степенного
ряда ![]() .
.
Используем
формулу Коши-Адамара ![]() .
.
Область
сходимости имеет вид ![]() или
или ![]() .
.
Проверим
сходимость ряда на границах области:
при ![]() числовой
ряд
числовой
ряд  расходится,
т.к. не выполнено необходимое условие
расходится,
т.к. не выполнено необходимое условие
сходимости.
Аналогичный результат получим при 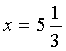 .
Следовательно, областью сходимости
данного ряда является интервал
.
Следовательно, областью сходимости
данного ряда является интервал 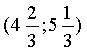 .
.
8. Свойства степенных рядов. Ряды Тейлора и Маклорена.
Свойства степенных рядов |
||||||
Отметим здесь, без доказательства, три важных свойства степенных рядов. 1.Сумма
является
непрерывной функцией в каждой точке
интервала сходимости 2.Ряд
полученный
почленным дифференцированием ряда
(2), является степенным рядом с тем же,
что и ряд (2), интервалом сходимости
.
Сумма ряда (4) Замечание.
Ряд (4) также можно почленно дифференцировать
и сумма полученного после этого ряда
равна 3.
Пусть числа
|
Разложение ф-ций в степ ряды Пусть
функция
где
–интервал
сходимости ряда (1). В этом случае
говорят, что функция
разлагается
в степенной ряд в окрестности точки
… … … … … … … … …
… … … … … … … … … Все
ряды имеют интервалы сходимости
.
При
Ряд
(2) называется рядом Тейлора для
функции
и называется рядом Маклорена. Таким образом, если функция является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции . Рассмотрим –ю частичную сумму ряда Тейлора:
Многочлен
(4) называется многочленом Тейлора
степени n.
Разность Теорема. Для
того, чтобы бесконечно дифференцируемая
в точке
функция
являлась
суммой составленного для нее ряда
Тейлора, необходимо и достаточно,
чтобы Можно показать, что остаточный член можно представить в форме Лагранжа:
Формула (5) называется формулой Тейлора, а ее частный случай при называется формулой Маклорена:
9. Разложение функций в ряд Тейлора. Остаточный член ряда. Большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
Ряд Тейлора в окрестности точки a имеет виды: 1)
2) k-тый
коэффициент (при хk) ряда определяется
формулой
Пример
12. Разложить в ряд Тейлора в
окрестности
Разложим
в ряд производную данной функции
Проинтегрировав
общий член полученного ряда, и, учитывая,
что y(0)=0,
получим искомое разложение:
|
||||||||||||
10. Применение степенных рядов для приближенных вычислений Степенные ряды широко применяются в приближённых вычислениях. Рассмотрим это на примерах.
Пример 1.
Вычислить
Воспользуемся
разложением
= - 0,0238+0,0046 –0,0008≈0,7475≈0,748. Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
Вычислить e0,1 с точностью до 0,001.
Для
функции ex формула
Тейлора имеет вид: ex=1+x+
При x=0.1
получаем знакоположительный числовой
ряд. Так как при этом с При x=0,1 получаем
e0,1≈1+0,1+ Так как 0,0002<0,0005, то достаточно взять четыре члена ряда.
Пример 4. Проинтегрировать дифференциальное уравнение y′=y+x2, y(0)=-2 методом последовательного дифференцирования. Будем искать решение в виде ряда Маклорена:
y(x)=y(0)+ Вычислим производные: y′=y+x2, y″=y′+2x, y″′=y″+2, y(4)= y″′, …, y(n)= y″′ при n=4, 5, … . При x=0 получаем: y(0)=-2, y′(0)=-2, y″(0)=-2, y(n)(0)=0 при n=3, 4, 5. Окончательно получаем y(x)=-2-2x-x2.
11. Сходимость по норме. Гильбертовы пространства
|
Сходимость
по норме
- сходимость последовательности { х п}в
нормированном векторном пространстве
Xк х,определяемая следующим
образом: ![]() если
если ![]() при
при ![]() Здесь
Здесь ![]() -
норма в X.
-
норма в X.
ГИЛЬБЕРТОВО
ПРОСТРАНСТВО -
комплексное векторное
пространство ,являющееся
бесконечномерным полным евклидовым
пространством. Это означает, что Г.
п. ![]() есть
множество элементов, на к-ром, помимо
операций векторного пространства
(сложения и умножения на число), задана
также комплекснозначная ф-ция от пары
аргументов х,
у из
,
есть
множество элементов, на к-ром, помимо
операций векторного пространства
(сложения и умножения на число), задана
также комплекснозначная ф-ция от пары
аргументов х,
у из
,![]() ,
обозначаемая (х,
у)и
удовлетворяющая след. условиям (аксиомам):
1)
,
обозначаемая (х,
у)и
удовлетворяющая след. условиям (аксиомам):
1) ![]() ;
(х,
x)=0лишь
при x=0; 2)
(х,
y+z)= (х,у)+ (x,z);
3)
;
(х,
x)=0лишь
при x=0; 2)
(х,
y+z)= (х,у)+ (x,z);
3) ![]() ,
, ![]() (x,у)=(у,х)*;
*означает
комплексное сопряжение (иногда
рассматривают вещественные Г. п., к-рые
являются векторными пространствами
над полем
(x,у)=(у,х)*;
*означает
комплексное сопряжение (иногда
рассматривают вещественные Г. п., к-рые
являются векторными пространствами
над полем ![]() и
удовлетворяют аксиоме 3 с
и
удовлетворяют аксиоме 3 с ![]() ).
Ф-ция (х,
у)наз.
скалярным или внутренним произведением.
В силу аксиомы 1 на
).
Ф-ция (х,
у)наз.
скалярным или внутренним произведением.
В силу аксиомы 1 на ![]() также
определена неотрицат. ф-ция
также
определена неотрицат. ф-ция ![]()
![]() ,
к-рая обладает всеми свойствами нормы
на векторном пространстве; по отношению
к ней
,
к-рая обладает всеми свойствами нормы
на векторном пространстве; по отношению
к ней ![]() является
нормированным и банаховым (т. е. полным
нормированным) пространством. Нередко
(напр., при квантовании эл--магн. поля)
приходится рассматривать пространства,
к-рые не являются полными в смысле
сходимости по норме
является
нормированным и банаховым (т. е. полным
нормированным) пространством. Нередко
(напр., при квантовании эл--магн. поля)
приходится рассматривать пространства,
к-рые не являются полными в смысле
сходимости по норме ![]() и
(или) допускают равенство (х,
x)=0 для
нек-рых
и
(или) допускают равенство (х,
x)=0 для
нек-рых ![]() Каждое
такое пространство наз. предгильбертовым;
существует стандартная процедура,
позволяющая достроить его до обычного
Г. п. Применения
Г. п.
В матем. и физ. приложениях возникают
разл. классы пространств, являющихся
обобщениями Г. п. Осн. область применений
этих пространств составляют ур-ния
матем. физики. Сфера применений Г. п.
в совр. физике почти необозрима. Г. п.-
центральный матем. объект, лежащий в
основе всего аппарата квантовой физики.
Представление множества состояний физ.
системы с помощью Г. п. есть фундам.
элемент матем. структуры в самом широком
спектре физ. теорий: квантовой механике,
квантовой статистич. физике, классич.
и квантовой теории поля; оно является
возможным также и в классич. механике.
Такой же универсальностью обладает и
представление наблюдаемых физ. систем
с помощью самосопряжённых операторов
в Г. п. Наиб. тесная связь, достигающая
почти полного сращивания между физ. и
матем. исследованием, сложилась между
аппаратом Г. п. и квантовой механикой.
Наконец, широкие и разнообразные
применения Г. п. находят при изучении
ур-ний матем. физики, описывающих разл.
физ. процессы.
Каждое
такое пространство наз. предгильбертовым;
существует стандартная процедура,
позволяющая достроить его до обычного
Г. п. Применения
Г. п.
В матем. и физ. приложениях возникают
разл. классы пространств, являющихся
обобщениями Г. п. Осн. область применений
этих пространств составляют ур-ния
матем. физики. Сфера применений Г. п.
в совр. физике почти необозрима. Г. п.-
центральный матем. объект, лежащий в
основе всего аппарата квантовой физики.
Представление множества состояний физ.
системы с помощью Г. п. есть фундам.
элемент матем. структуры в самом широком
спектре физ. теорий: квантовой механике,
квантовой статистич. физике, классич.
и квантовой теории поля; оно является
возможным также и в классич. механике.
Такой же универсальностью обладает и
представление наблюдаемых физ. систем
с помощью самосопряжённых операторов
в Г. п. Наиб. тесная связь, достигающая
почти полного сращивания между физ. и
матем. исследованием, сложилась между
аппаратом Г. п. и квантовой механикой.
Наконец, широкие и разнообразные
применения Г. п. находят при изучении
ур-ний матем. физики, описывающих разл.
физ. процессы.
Примеры
Евклидово пространство.
Пространство
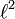 .
Его точки суть бесконечные последовательности
вещественных чисел
.
Его точки суть бесконечные последовательности
вещественных чисел 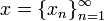 ,
для которых сходится ряд
,
для которых сходится ряд 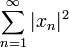 .
Скалярное произведение на этом
пространстве задаётся равенством
.
Скалярное произведение на этом
пространстве задаётся равенством
![]() .
.

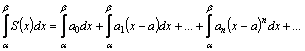
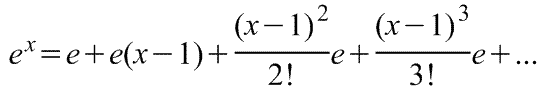
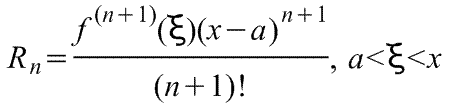
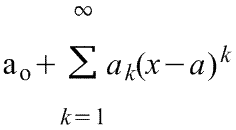
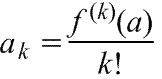
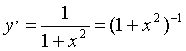 ,
воспользовавшись табличным разложением
для функции
,
воспользовавшись табличным разложением
для функции 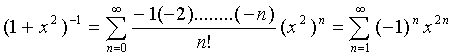 .
.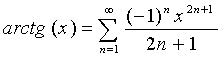 .
.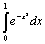 с
точностью до 0,001.
с
точностью до 0,001.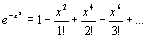 Тогда
Тогда