16. Дивергенция векторного поля. Формула Остроградского

Дивергенция (от лат. divergere — обнаруживать расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле» (точнее — насколько расходятся входящий и исходящий поток).

Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учетом знака. Поэтому можно дать более короткое определение дивергенции:

дивергенция — это дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.

Оператор дивергенции к полю F: divF

Определение дивергенции выглядит так:

где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объема ее внутренности). В обоих случаях подразумевается, что

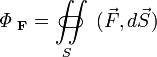
Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением

С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или стоком этого поля:

— точка поля является источником;