8. Главные кривизны поверхности

Пусть Φ есть регулярная поверхность в трёхмерном евклидовом пространстве. Пусть p — точка Φ, Tp — касательная плоскость к Φ в точке p, n — единичная нормаль к Φ в точке p, а — πe плоскость, проходящая через n и некоторый единичный вектор e в Tp. Кривая γe, получающаяся как пересечение плоскости πe с поверхностью Φ, называется нормальным сечением поверхности Φ в точке p в направлении e. Величина

где обозначает скалярное произведение, а k — вектор кривизны γe в точке p, называется нормальной кривизной поверхности Φ в направлении e. С точностью до знака нормальная кривизна равна кривизне кривой γe.

В касательной плоскости Tp существуют два перпендикулярных направления e1 и e2 такие, что нормальную кривизну в произвольном направлении можно представить с помощью так называемой формулы Эйлера:

κe = κ1cos 2α + κ2sin 2α

где α — угол между e1 и e, a величины κ1 и κ2 нормальные кривизны в направлениях e1 и e2, они называются главными кривизнами, а направления e1 и e2 — главными направлениями поверхности в точке p. Главные кривизны являются экстремальными значениями нормальных кривизн. Структуру нормальных кривизн в данной точке поверхности удобно графически изображать с помощью индикатрисы Дюпена.

Величина

H = κ1 + κ2

называется средней кривизной поверхности. Величина

K = κ1κ2

называется гауссовой кривизной поверхности.

Гауссова кривизна является объектом внутренней геометрии поверхностей, в частности не изменяется при изометрических изгибаниях.

9. Теорема (формула) Стокса

Пусть на ориентируемом многообразии M размерности n заданы ориентируемое p-мерное подмногообразие σ и дифференциальная форма ω степени p − 1 класса C1

Тогда, если граница подмногообразия положительно ориентирована, то

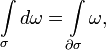
где dω обозначает внешний дифференциал формы ω.

Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия M.

Частный случай – формула Ньютона-Лейбница.

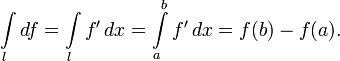
10. Теорема (формула) Остроградского

Фо́рмула Острогра́дского — формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

то есть интеграл от дивергенции векторного поля F, распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

11. Скалярные поля. Поверхности уровня

Если каждой точке M области многомерного пространства поставлено в соответствие некоторое (обычно — действительное) число u, то говорят, что в этой области задано скалярное поле. Другими словами, скалярное поле — это функция, отображающая Rn в R (скалярная функция).

Примеры пространственных скалярных полей: температура (подразумевается, что она вообще говоря разная в разных точках пространства); электростатический потенциал; потенциал в ньютоновской теории тяготения; поле давления в жидкой среде.

Пример плоского поля: глубина моря, отмеченная каким-либо образом на плоской карте.

Обычно под скалярным полем понимается поле, инвариантное при преобразованиях координат (иногда, и нередко — при определенном классе преобразований координат, например, при преобразованиях, сохраняющих объем, ортогональных преобразованиях и т. п.; но не менее редко имеется в виду инвариантность скалярного поля при произвольных преобразованиях координат, ограниченных, быть может, только гладкостью). (См. скаляр).

В этом смысле далеко не каждая вещественнозначная функция координат является скалярным полем. Простейший пример: в этом смысле не является скалярным полем одна из координатных компонент векторного поля, так как при изменении выбора координат (например, при повороте координатных осей) она не останется неизменной (то есть не является инвариантом преобразований координат).

Под скалярным полем в современной теоретической физике понимается (также, и в особенности) обычно фундаментальное поле скаляра пространства Минковского (лоренц-инвариантное поле) или поле, инвариантное относительно общекоординатных преобразований, (обычно первое и второе практически совпадает).

Практическими синонимами термина скалярное поле в этом смысле являются термины поле спина ноль частица спина ноль, скалярная частица (последние, всё же несколько разводя эти близкие понятия, называют также возбуждениями скалярного поля).

Экспериментально (пока) не открыто ни одно фундаментальное скалярное поле. Однако такие поля играют немалую роль в теоретических построениях (существуют важные гипотетические скалярные поля, например, поле Хиггса), а также их наличие (наряду с векторными и тензорными полями, понимаемыми в том же смысле и наблюдаемыми реально) необходимо для полноты классификации фундаментальных полей.