6. Линейная парная регрессия. Уравнение парной регрессии по выборке. Смысл коэффициентов регрессии.

Если функция регрессии линейна, то речь ведут о линейной регрессии. Модель линейной регрессии является наиболее распространенным (и простым) уравнением зависимости между экономическими переменными. Кроме того, построенное линейное уравнение может

быть начальной точкой эконометрического анализа. линейная регрессия (тео-

ретическое линейное уравнение регрессии) представляет собой линей-

ную функцию между условным математическим ожиданием M(YX =

= xi) зависимой переменной Y и одной объясняющей переменной X.

M(YX = xi) = β0 + β1xi. (4.5)

Отметим, что принципиальной в данном случае является линейность по параметрам β0 и β1 уравнения.

Для отражения того факта, что каждое индивидуальное значе-

ние yi отклоняется от соответствующего условного математического

ожидания, необходимо ввести в соотношение (4.5) случайное слагае-

мое εi.

yi = M(YX = xi) + εi = β0 + β1xi + εi. (4.6)

Соотношение (4.6) называется теоретической линейной регрес-

сионной моделью; β0 и β1 − теоретическими параметрами (теорети-

ческими коэффициентами) регрессии; εi − случайным отклонением. эмпирическое уравнение регрессии

y) i = b0 + b1xi ,

где i − оценка условного математического ожидания M(YX = xi); b0

и b1 − оценки неизвестных параметров β0 и β1, называемые эмпирическими коэффициентами регрессии. Следовательно, в конкретном

случаеy )

yi = b0 + b1xi + ei, (4.9)

где отклонение еi − оценка теоретического случайного отклонения εi. В силу несовпадения статистической базы для генеральной совокупности и выборки оценки b0 и b1 практически всегда отличаются от истинных значений коэффициентов β0 и β1, что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок.

7.Предпосылки классической линейной регрессионной модели

метод нахождения коэффициентов, при котором минимизируется сумма квадратов отклонений . Он получил название метод наименьших квадратов (МНК). Этот метод оценки является наиболее простым с вычислительной точки зрения. Кроме того, оценки коэффициентов регрессии, найденные МНК при определенных предпосылках, обладают рядом оптимальных свойств. Для того, чтобы полученные по МНК оценки обладали некоторыми полезными статистическими свойствами, необходимо выполнение ряда предпосылок относительно оцениваемой модели, называемыми условиями Гаусса-Маркова Это из 4 вопроса

Предпосылки МНК (условия Гаусса-Маркова)

1. Математическое ожидание случайного отклонения е_i равно нулю: M(е_i) = 0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В определенном наблюдении случайный член может быть положительным или отрицательным, но он не должен иметь систематического смещения. Выполнимость M(е_i) = 0 влечет выполнимость:

2. Дисперсия случайных отклонений epsiloni постоянна: D(εi) = D (εj ) = σ² = const для любых наблюдений i и j.

Условие независимости дисперсии ошибки от номера наблюдения называется гомоскедастичностью (homoscedasticity). Невыполнимость этой предпосылки называется гетероскедастичностью (heteroscedasticity).

Поскольку D(ε)=M((εj - Mεj))² = M(ε²), то эту предпосылку можно переписать в форме: M(е²_i) = σ². Причины невыполнимости данной предпосылки и проблемы, связанные с этим, подробно рассматриваются ниже.

3. Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j.

Выполнимость этой предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.

Выполнимость данной предпосылки влечет следующее соотношение:

Если данное условие выполняется, то можно говорить об отсутствии автокорреляции. С учетом выполнимости предпосылки 1 данное соотношение можно переписать в виде:

Причины невыполнимости этой предпосылки и проблемы, связанные с ними, рассматриваются ниже.

4. Случайное отклонение должно быть независимо от объясняющих переменных.

Обычно это условие выполняется автоматически, если объясняющие переменные не являются случайными в модели.

Данное условие предполагает выполнимость следующего соотношения:

Заметим, что выполнимость этой предпосылки не столь критична для эконометрических моделей.

5. Модель является линейной относительно параметров.

Для случая множественной линейной регрессии существенными являются еще две предпосылки.

6. Отсутствие мультиколлинеарности.

Между объясняющими переменными отсутствует сильная линейная зависимость.

7. Случайные отклонения εi, i = 1, 2, ... , n, имеют нормальное распределение.

Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Но, являясь лишь оценками, они не позволяют сделать вывод, насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей генеральной совокупности, насколько

близки оценки b0 и b1 коэффициентов своим теоретическим прототипам β0 и β1, как близко оцененное значение i y ) к условному математическому ожиданию M(YX = xi), насколько надежны найденные оценки. Для ответа на эти вопросы необходимы определенные дополнительные исследования.

Как следует из соотношения (4.6), значения уi зависят от значений xi и случайных отклонений εi. Следовательно, переменная Y является случайной величиной, напрямую связанной с εi. Это означает, что до тех пор, пока не будет определенности в вероятностном поведении εi, мы не сможем быть уверенными в качестве оценок. Действительно, можно показать, что оценки коэффициентов регрессии – случайные величины, зависящие от случайного члена в уравнении регрессии.

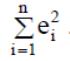
Предпосылки МНК (условия Гаусса−Маркова)

10. Математическое ожидание случайного отклонения ε

i равно

нулю: M( ε

i) = 0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не

оказывает влияния на зависимую переменную. В каждом конкретном

наблюдении случайный член может быть либо положительным, либо

отрицательным, но он не должен иметь систематического смещения.

Отметим, что выполнимость M(εi) = 0 влечет выполнимость

M(YX = = xi) = β0 + β1xi.

20. Дисперсия случайных отклонений ε

i постоянна:

Данное условие подразумевает, что несмотря на то, что при каж-

дом конкретном наблюдении случайное отклонение может быть либо

большим, либо меньшим, не должно быть некой априорной причины,

вызывающей большую ошибку (отклонение).

Выполнимость данной предпосылки называется гомоскедастич-

ностью (постоянством дисперсии отклонений). Невыполнимость

данной предпосылки называется гетероскедастичностью (непосто-

янством дисперсий отклонений).

Поскольку D(εi) = M(εi − M(εi))2 = M(е2 )i , то данную предпосылку

можно переписать в форме: M(е2 )i = σ2.

30. Случайные отклонения εi и εj являются независимыми

друг от друга для i ≠ j.Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Другими словами, величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любо-

го другого отклонения.

Выполнимость данной предпосылки влечет следующее соотно-

шение:

Поэтому, если данное условие выполняется, то говорят об отсут-

ствии автокорреляции. С учетом выполнимости предпосылки 10 соот-

ношение (5.6) может быть переписано в виде: M(εi εj) = 0 (i ≠ j).

40. Случайное отклонение должно быть независимо от объясняющих переменных.

Обычно это условие выполняется автоматически при условии,

что объясняющие переменные не являются случайными в данной мо-

дели.

Данное условие предполагает выполнимость следующего соот-

ношения:

уеixi = cov(εi, xi) = M((εi − M(εi))(xi − M(xi))) = M(εi(xi − M(xi))) =

= M(εi xi) − M(εi) M(xi) = M(εi xi) = 0.

Следует отметить, что выполнимость данной предпосылки не

столь критична для эконометрических моделей.

50. Модель является линейной относительно параметров_