
- •Вопросы к экзамену по математическому анализу.
- •1.Определение определенного интеграла.
- •2.Необходимое условие существования определенного интеграла
- •3. Нижняя и верхняя интегральные суммы Дарбу и их свойства.
- •4. Необходимое и достаточное условие существования определенного интеграла.
- •5. Некоторые классы функций для которых существует определенный интеграл
- •6. Некоторые свойства определённого интеграла
- •7.Определение интеграла с переменным верхним пределом.
- •8.Опредидение интеграла с переменным верхним пределом.
- •9. Формула Ньютона-Лейбница.
- •10. Замена переменной в определённом интеграле
- •11. Интегрирование по частям в определенном интеграле
- •12. Понятие квадрируемой фигуры и её площади.
- •13. Свойства квадрируемых фигур.
- •14. Понятие спрямляемой плоской кривой и её длины. Достаточное условие спрямляемости плоской кривой(сформулировать теорему).
- •15. Вычисление объёма тела вращения(с рисунком).
- •16.Вычисление площади поверхности вращения.
- •17. Определение несобственного интеграла первого рода и его свойства.
- •18. Определение несобственного интеграла второго рода и его свойства.
- •19. Понятие n-мерного Евклидова пространства.
- •20. Множества в пространстве .
- •21. Понятие действительной функции нескольких действительных переменных.
- •22. Действительная функция двух действительных переменных.
- •23. Предел функции двух действительных переменных . Повторные пределы.
- •24. Непрерывность функции двух действительных переменных.
- •25. Определение частной производной функции двух переменных. Механический смысл.
- •26. Определение дифференцируемой функции двух действительных переменных и полного дифференциала. Необходимое условие дифференцируемости функции двух действительных переменных.
- •27. Достаточное условие дифференцируемости двух действительных переменных.
- •28.Дифференцирование сложной функции.
- •29. Частные производные высших порядков.
- •30. Восстановление функции по её полному дифференциалу.
- •31. Дифференциалы высших порядков для функции двух переменных.
- •32. Определение производной по направлению. Теорема.
- •33. Градиент функции. И его свойства.
23. Предел функции двух действительных переменных . Повторные пределы.
Пусть
определена на множестве R
плоскости
 и точка (
и точка ( -
предельная точка множества Д.
-
предельная точка множества Д.
Определение:
Число А
называется пределом функции
 в точке (
,
если для любого
в точке (
,
если для любого
 такое что если будут выполнятся
неравенства
такое что если будут выполнятся
неравенства
 то при таких
будет
выполнятся неравенство:
то при таких
будет
выполнятся неравенство:

Обозначение:

Наряду с рассмотрением
предела функции двух переменных, для
функции двух переменных рассматривают
повторные пределы. Пусть при каждом
фиксированном x
существует
 Этот предел будет являться функцией
переменной Х. То есть существует
Этот предел будет являться функцией
переменной Х. То есть существует
 Этот предел называется повторным
пределом для функции
Этот предел называется повторным
пределом для функции
 в точке
в точке
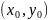
Аналогично вводится
повторный предел

24. Непрерывность функции двух действительных переменных.
Теорема: Пусть
1.
Существует
 и существует
и существует
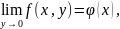 то существует повторный предел
то существует повторный предел

2.
Существует
 существует
существует
 то существует
повторный предел
то существует
повторный предел
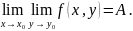
Пусть функция
определена в области Д и точка (
и точка ( Д.
Д.
Определение:
Функция
называется непрерывной в точке (
если

Определение:
Функция
называется непрерывной в точке (
если
 такое что
если выполняется
такое что
если выполняется
 то выполняется неравенство:
то выполняется неравенство: .
.
Пусть точка
 тогда разности
тогда разности
 называют
приращениями независимых переменных
(
при переходе от точки (
к точке
называют
приращениями независимых переменных
(
при переходе от точки (
к точке
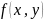 .
Отсюда
.
Отсюда
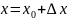 ,
,
 , разность
, разность
 называется
полным приращением функции при переходе
от точки (
к точке
.Тогда
определение непрерывности функции в
точке будет таким:
называется
полным приращением функции при переходе
от точки (
к точке
.Тогда
определение непрерывности функции в
точке будет таким:
 ;
;
Определение:
Функция
называется непрерывной в области Д,
если она непрерывна в каждой точке
 принадлежащей области Д.
принадлежащей области Д.
25. Определение частной производной функции двух переменных. Механический смысл.
Пусть функция
определена в области Д плоскости
и пусть
.
Координате х дадим приращение
 , а координату у оставим без изменения,
получим точку
, а координату у оставим без изменения,
получим точку
 .
Запишем тогда приращение функции
.
Запишем тогда приращение функции
 -его
называют частным приращением функции
при переходе от точки
-его
называют частным приращением функции
при переходе от точки

Определение:
Если
существует конечный предел
 ,
то этот предел называют частной
производной функции
в точке
по переменной х.
,
то этот предел называют частной
производной функции
в точке
по переменной х.
Обозначение:
 ;
;
Если хотят указать
конкретную точку
то пишут
 Итак по определению
Итак по определению

Аналогично
определяется частная производная
функции
по переменной y,
а именно

Механический
смысл частных
производных
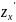 и
и
 это
скорость изменения значений функции
в точке
вдоль осей
и
соответственно, в положительном
направлении.
это
скорость изменения значений функции
в точке
вдоль осей
и
соответственно, в положительном
направлении.
Чтобы вычислить частную производную функции по одной из переменных нужно на данный момент остальные переменные считать постоянными и находить производную функции от одной переменной.
26. Определение дифференцируемой функции двух действительных переменных и полного дифференциала. Необходимое условие дифференцируемости функции двух действительных переменных.
Пусть функция
определена в области Д плоскости
и пусть
.
Переменным х и у дадим приращение
и
 . И запишем полное приращение функции
. И запишем полное приращение функции

Определение: функция называется дифференцируемой в точке , если её полное приращение представимо в виде:
 -(1)
-(1)
Где А и В не зависят
от
и
а
 ,
,

-(1) называют условием дифференцируемости функции в точке .
Пусть для функции
выполняется условие дифференцируемости
(1) , тогда выражение
 называется полным
дифференциалом функции
в точке
называется полным
дифференциалом функции
в точке

Обозначение:
 .
.
Теорема: Если функция дифференцируема в точке то она непрерывна в этой точке.
Доказательство.
Воспользуемся определением непрерывности
в виде
 ;
Так как по
условию функция
дифференцируема в точке
то выполняется условие (1), получим :
;
Так как по
условию функция
дифференцируема в точке
то выполняется условие (1), получим :
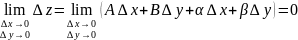 следовательно по определению функция
непрерывна в точке (
следовательно по определению функция
непрерывна в точке (
Доказано.
Теорема: Если функция дифференцируема в точке то она имеет в этой точке частные производные.
