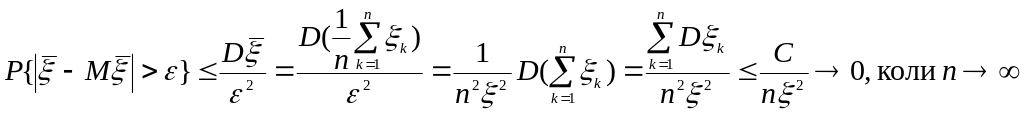- •Простір елементарних подій. Випадкові події, операції над ними.
- •Імовірності в дискретних просторах елементарних подій.
- •Дати частотне та класичне означення імовірності та вказати властивості імовірностей.
- •Дати геометричне означення імовірності. Задача Бюффона.
- •Центральна гранична теорема.
- •Емпірична функція розподілу.
- •Гістограма та полігон частот.
- •Статистичне оцінювання невідомих параметрів розподілів. Властивості оцінок.
- •Двофакторний дисперсійний аналіз.
- •Аналіз часових рядів. Виділення тренду.
T I T M C _ H A N D B O O K
Простір елементарних подій. Випадкові події, операції над ними.
Стохастичний експеримент – експеримент, який можна повторювати будь-яку кількість разів і наслідки якого не можна передбачити наперед. (наприклад підкидання монети, грального кубика)
![]() (омега велике) – усі можливі
наслідки стохастичного експерименту
– простір елементарних подій.
(омега велике) – усі можливі
наслідки стохастичного експерименту
– простір елементарних подій.
![]()
![]() –
елементарний наслідок або
елементарна подія
–
елементарний наслідок або
елементарна подія
Операції над подіями:
Доповнення:

Об’єднання:
 *
*
*
![]() – диз’юнкція
– „або”
– диз’юнкція
– „або”
Перетин/переріз:
 **
**
**
![]() – кон’юнкція
– „і”
– кон’юнкція
– „і”
Різниця:
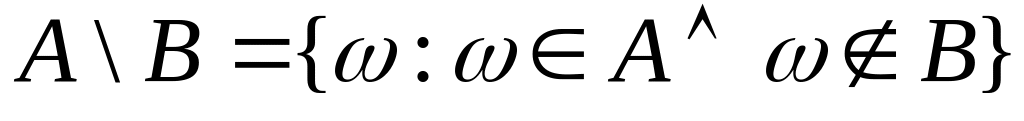
Зв’язок між подіями
1. Правило Де-Моргана:

2. (різниця через перетин):
![]()
Імовірності в дискретних просторах елементарних подій.
– дискретна множина
![]() має імовірність
має імовірність
![]()
![]()
![]()
Нехай
![]()
![]()
Дати частотне та класичне означення імовірності та вказати властивості імовірностей.
Нехай є довільний стохастичний експеримент
![]() – частота події А;
Скільки разів подія А
з’явилася при n
повтореннях цього експерименту;
– частота події А;
Скільки разів подія А
з’явилася при n
повтореннях цього експерименту;
![]()
Імовірність
![]()
Властивості:
1.
![]()
2.
![]() – достовірна подія
– достовірна подія
3. Нехай є дві події А,В,
![]() ,
то
,
то
![]()
Частотне означення імовірності (або озн. імов. Мізеса)
Якщо існує границя
![]() – імовірність події А;
при цьому подія А
– стохастично стійка.
– імовірність події А;
при цьому подія А
– стохастично стійка.
Недоліки такого означення:
![]() (неможливо
зробити
(неможливо
зробити
![]() експериментів);
якщо не існує границі – не існує
імовірності.
експериментів);
якщо не існує границі – не існує
імовірності.
Класичне означення імовірності (XVI-XVII ст.)
Нехай
– скінченний простір. (![]() )
і всі елементарні наслідки рівноможливі
(
)
і всі елементарні наслідки рівноможливі
(![]() );
тоді якщо
);
тоді якщо
![]() ,
то
,
то

![]() – імовірність довільной
події А
дорівнює число m
події А
поділити на загальну кількість точок.
– імовірність довільной
події А
дорівнює число m
події А
поділити на загальну кількість точок.
Дати геометричне означення імовірності. Задача Бюффона.
![]() (Евклідовий
простір)
(Евклідовий
простір)
![]() ,
міра – довжина
,
міра – довжина
![]() 2х
мірний, міра – площа
2х
мірний, міра – площа
![]() 3х
мірний, міра – об’єм
3х
мірний, міра – об’єм
Міра Лебега
![]()
![]()
![]()
Властивості:
1)
![]()
2)
![]()
3)
![]()
Задача Бюффона
Нехай є простір розчерчений паралельними прямими, відстань між прямими – 2а. На цю площину довільним чином кидається голка довжиною 2l. Яка імовірність того, що голка перетне одну з прямих?

(що можна використати для
наближенного обчислення
![]() )
)
![]()
Аксіоми теорії імовірностей.
Аксіома1:
![]()
А2:
![]()
А3 (зліченої адитивності):
![]() ,
,
![]()
![]()
А4 (скінченної адитивності):
![]()
Властивості імовірностей.
1)
![]()
2)
![]()
3)
![]()
![]()
4)
![]()
5) (наслідок 4ї):
![]()
6) Теорема додавання імовірностей:
![]()
Умовні імовірності. Приклад.
![]() – А при
умові В
– А при
умові В
Формальне означення:
![]()
Формула множення імовірностей:
![]()
Довести формулу повної імовірності.
![]() – повна група подій, якщо:
– повна група подій, якщо:
1)
![]()
2)
![]()
![]()
Доведення:
![]()
Довести формулу Байеса.
Формула Байеса

![]() – апріоні імовірності
– апріоні імовірності
![]() – апостеріорні імовірності
– апостеріорні імовірності
Незалежні події. Властивості незалежних подій.
1) А і
В –
незалежні, якщо
![]()
2)
![]()
Незалежність в сукупності
![]() називаються незалежними в
сукупності, якщо для будь-якого цілого
називаються незалежними в
сукупності, якщо для будь-якого цілого
![]() для будь-яких k
подій
для будь-яких k
подій
![]() імовірність перетину
імовірність перетину
![]()
Математичне сподівання дискретних випадкових величин.
Математичне сподівання – середнє ймовірнісне значення випадкової величини.
![]()
Властивості.
Властивості математичного сподівання:
1. Якщо
![]() ,
то
,
то
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6. Якщо
![]() і
і
![]() – незалежні, то
– незалежні, то
![]()
7. Математичне сподівання функції від випадкової величини:
![]()
Дисперсія дискретних випадкових величин. Властивості.
Дисперсія – середньоквадратичне відхилення випадкової величини від свого математичного сподівання
![]()
Властивості дисперсії
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5. Якщо
і
– незалежні, то
![]()
Коефіцієнт кореляції випадкових величин. Властивості.
Коефіцієнт кореляції – міра залежності випадкових величин
![]()
![]()
Властивості:
1. Якщо
![]() – незалежні, то
– незалежні, то
![]()
2.
![]()
3.
![]() – лінійна залежність (найсильніша)
– лінійна залежність (найсильніша)
![]() – пряма залежність
– пряма залежність
![]() – обернена залежність
– обернена залежність
Зауваження: З того, що не випливає незалежність випадкових величин.
Локальна та інтегральна теорема Муавра-Лапласа та їх застосування.
Локальна теорема Муавра-Лапласа:
Якщо
![]() ,
тоді
,
тоді
![]() ,
де
,
де
![]()
![]() ,
де
,
де
![]() (функція
Лапласа)
(функція
Лапласа)
Інтегральна теорема Муавра-Лапласа:
![]()


![]() – інтегральна функція Лапласа
– інтегральна функція Лапласа
![]()
![]()
Використовується якщо
![]() або
або
![]() (конспект)
(конспект)
Теорема Пуассона та її застосування.
Якщо
![]() ,
то
,
то
![]()
![]()
Використовується якщо
![]() (конспект)
(конспект)
Біномінальний розподіл. Обчислити
 .
.
n – кількість експериментів
p – імовірність успіху
q – імовірність неудачі
![]()
– загальне число успіхів в n експериментах
![]()
![]()
m – найбільш імовірне число успіхів
![]()
Математичне сподівання:

Дисперсія:

![]()
Геометричний розподіл. Обчислити .
Імовірність успіху – p, невдачі – q. Експерименти проводяться до першої появи успіху;
– кількість послідовних неудач.
![]()
![]()

![]()
Пуассонівський розподіл. Обчислити .

![]() - додатнє число, параметр
розподілу
- додатнє число, параметр
розподілу
![]()

![]()
Функції розподілу випадкових величин. Властивості.
![]() – функція розподілу
– функція розподілу
Властивості:
1)
![]()
2)
![]() – неперервна зліва
– неперервна зліва
3)
– неспадна:
![]()
4)
![]()

5) Якщо a, b – точки неперервності F(x), то
![]()
6)
![]()
якщо а
– точка неперервності, то
![]()
Щільність випадкових величин. Властивості.
![]() ,
де
,
де
![]() щільність
неперервної випадкової величини.
щільність
неперервної випадкової величини.
Властивості:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
Математичне сподівання та дисперсія неперервних випадкових величин.
Математичне сподівання:
![]()
Властивості:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
6) Якщо
і
– незалежні, то
![]()
![]()
Дисперсія:
![]()
![]()
Рівномірний розподіл на відрізку [a, b]. Обчислити .
![]()
![]()
![]()
![]()
Показниковий розподіл. Обчислити .
![]()
![]()
![]()
![]()
Нормальний розподіл. Обчислити
 .
.
![]()

 – дзвіноподібна функція
– дзвіноподібна функція
Якщо
![]() ,
,
![]() ,
то розподіл стандартний
,
то розподіл стандартний
![]()
Нормальний розподіл. Обчислити
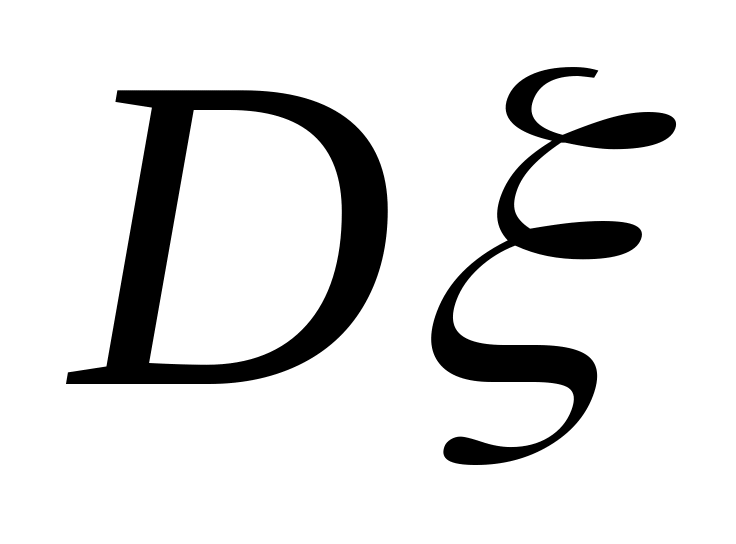 .
.
– дзвіноподібна функція
Якщо , , то розподіл стандартний
![]()
Довести нерівність Чебишева.
Нерівність Чебишева:
Нехай для
існує
![]()
Тоді для
![]()

Правило 3![]() :
Нехай
,
тоді
:
Нехай
,
тоді
![]()
Закон великих чисел. (Теорема Хінчина, теорема Чебишева).
Будь-яке твердження про збіжність середньоарифметичних випадкових величин називається законом великих чисел.
![]()
Теорема Хінчина:
Нехай
![]() – послідовність незалежних, однаково
розподілених випадкових величин
(п.н.о.р.в.в.)
– послідовність незалежних, однаково
розподілених випадкових величин
(п.н.о.р.в.в.)
![]()
Тоді
![]()
Теорема Чебишева:
Нехай – п.н.в.в.
![]()
![]()
Тоді:
![]()
Доведення теореми Чебишева: