§ 3.7. Поворот осей координат
В аналитической геометрии часто применяется преобразование координат, называемое поворотом осей. Оно заключается в следующем: обе оси координат поворачиваются в одну сторону на один и тот же угол, а начало координат остается неизменным. Примеры использования этого преобразования будут даны в следующих двух параграфах.
Пусть
оси координат повернуты на угол
(рис. 3.14). Угол
– это угол, на который нужно повернуть
старую ось
до ее совмещения с новой осью
;
угол
считается положительным при повороте
против часовой стрелки.
Выведем
формулы, позволяющие выразить старые
координаты
и
любой точки
через ее новые координаты
и
.
Для
этого построим радиус-вектор
точки
и обозначим через
и
углы, образованные им соответственно
с осями
и
:
точка
имеет полярные координаты
и
,
если за полярную ось принять ось
,
и координаты
и
,
если за полярную ось принять ось
.
Углы
,
и
связаны равенством
.
Выражая декартовы координаты точки
через ее полярные координаты, имеем:
(А)
(Б)
Заменяя
в формулах (А)
на
и используя формулы для синуса и косинуса
суммы двух углов, находим:
,
.
Отсюда, используя формулы (Б), находим следующие формулы, выражающие старые координаты и через новые координаты и :
(3.42)
.
Формулы обратного
перехода, выражающие новые координаты
через старые, мы получим аналогичным
путем из формул (Б), заменяя в них угол
на
:
(3.42')
.
Формулы (3.42') можно получить также из соотношений (3.42), рассматривая их как уравнения, определяющие и через и , и разрешая их относительно и .
Формулы
(3.42')
можно было бы получить из формул (3.42)
еще и следующим путем: поменять в формулах
(3.42) местами
и
,
а также
и
и заменить
на
(так как новые оси получаются из старых
поворотом на угол
,
то и старые оси могут быть получены из
новых поворотом в обратную сторону, т.
е. на угол
).
Рекомендуем читателю получить формулы (3.42') этими двумя способами.
§ 3.9. Исследование общего уравнения кривой второго порядка Наиболее общее уравнение второй степени относительно и имеет вид:
(3.49)
.
В аналитической геометрии его называют общим уравнением кривой второго порядка. От уравнения:
уравнение
(3.49) отличается наличием члена с
произведением координат, т. е. коэффициент
мы считаем не равным нулю.
В
настоящем параграфе наша задача –
показать, что и уравнение (3.49), так же,
как и уравнение (3.39), может определять
только одну из изученных нами ранее
кривых – эллипс, гиперболу или параболу
(с возможными для каждого из них случаями
вырождения), найти способ по виду
уравнения (3.49) установить тип определяемой
им кривой (подобно тому, как это делалось
для уравнения (3.39) по знаку произведения
)
и научиться для каждого конкретного
уравнения (3.49) строить кривую.
Наиболее простой способ решения этой задачи – при помощи поворота координатных осей на некоторый угол преобразовать уравнение (3.49) в уравнение вида (3.39) по отношению к новой системе координат, поскольку уравнение (3.39) нами уже изучено во всех подробностях.
Итак,
повернем координатные оси на некоторый
угол
.
Новые оси координат обозначим через
и
.
Тогда старые координаты будут выражаться
через новые по формулам (3.42) так:
,
.
Подставляя эти значения и в уравнение (3.49), после приведения подобных членов приведем его к виду:
(3.50)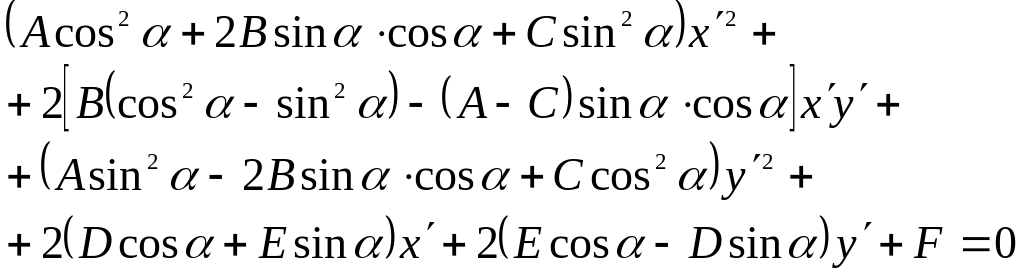
Уравнение (3.50) имеет ту же структуру, что и уравнение (3.49). его можно записать в виде:
(3.50')
где
(3.51)
(Значения
новых коэффициентов
и
,
несущественные для дальнейшего, мы не
описываем.)
Выберем теперь угол таким, чтобы новый коэффициент в уравнении (3.50') обратился бы в нуль; это дает нам для определения угла уравнение:
(3.52)
откуда находим:
(3.53)
Формула (3.53) определяет два значения угла , разность между которыми равна ; поэтому безразлично, какое из них выбрать: переход от одного к другому равносилен перестановке новых осей координат и .
После того, как угол определен по формуле (3.53), уравнение (3.50') приводится к виду:
(3.54)
и,
как нам известно, определяет эллипс
(окружность), гиперболу или параболу
(или вырождения этих кривых) в зависимости
от знака произведения
(см. § 3.6.).