1. Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

2. Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы допускают следующие алгебраические операции:

• сложение матриц, имеющих один и тот же размер;

• умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);

• умножение матрицы на элемент основного кольца или поля (т. е. скаляр).

Операции над матрицами

• Умножение матрицы на число

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

• Свойства умножения матриц на число

1. 1*A = A;

2. (Λβ)A = Λ(βA)

3. (Λ+β)A = ΛA + βA

4. Λ(A+B) = ΛA + ΛB

• Сложение матриц

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

• Свойства сложения матриц

5.коммутативность;

6.ассоциативность;

7.сложение с нулевой матрицей;

8.существование противоположной матрицы;

Все свойства линейных операций , повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров MxN образуют линейное пространство над полем P(полем всех действительных или комплексных чисел), поэтому каждая матрица является и вектором этого пространства.

• Умножение матриц

Умножение матриц (обозначение: AB, реже со знаком умножения  ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность  , B —  , то размерность их произведения AB = C есть  .

• Свойства умножения матриц

1.Ассоциативность;

2.произведение не коммутативно;

3.произведение коммутативно в случае умножения с единичной матрицей;

4.справедливость дистрибутивного закона;

5.(ΛA)B = Λ(AB) = A(ΛB);

• Комплексное сопряжение

Если элементами матрицы A = (a_ij) являются комплексные числа, то комплексно сопряжённая (не путать с эрмитово сопряжённой! см. далее) матрица равна  . Здесь   — число,комплексно сопряжённое к a.

• Транспонирование и эрмитово сопряжение

Транспонирование уже обсуждалось выше: если A = (a_ij), то A^T = (a_ji). Для комплексных матриц более употребительно эрмитово сопряжение:  . С точки зрения операторного взгляда на матрицы, транспонированная и эрмитово сопряжённая матрица — это матрицы оператора, сопряжённого относительно скалярного или эрмитова произведения, соответственно.

3. Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Свойства определителей

• Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):   , где   и т. д. — строчки матрицы,   — определитель такой матрицы.

• При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

4. Алгебраическим дополнением элемента 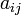  матрицы   называется число

,

где   — дополнительный минор, определитель матрицы, получающейся из исходной матрицы   путем вычёркивания i -й строки и j -го столбца.

Название «алгебраическое дополнение» связано с формулами разложения определителя матрицы по строке (по столбцу):

Лемма о фальшивом разложении определителя утверждает, что

при   и  .

Из этих утверждений следует алгоритм нахождения обратной матрицы:

• заменить каждый элемент исходной матрицы на его алгебраическое дополнение,

• транспонировать полученную матрицу - в результате будет получена союзная матрица,

• разделить каждый элемент союзной матрицы на определитель исходной матрицы.

5. Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Свойства обратной матрицы

• , где   обозначает определитель.

• для любых двух обратимых матриц A и B.

• где * ^T обозначает транспонированную матрицу.

• для любого коэффициента   .

• Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

6. Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).