Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Южно-Уральский государственный университет»

Факультет «Приборостроительный»

Кафедра «Автоматика и управление»

РЕФЕРАТ

по курсу

"Общая теория связи"

Выполнил:

студент группы ПС–317

______________С.С. Плотников

«____»________________2020 г.

Проверила:

______________Т.А. Барбасова

«____»________________2020 г.

Челябинск 2020

Оглавление

1 Распределение энергии в спектре периодического и непериодического сигнала; равенство Парсеваля; понятие о практической ширине частотного спектра сигнала.............................................................................................................................3 2 Принимаемый сигнал – как случайный процесс; виды случайных процессов, законы и числовые характеристики; корреляционные характеристики и свойства процессов; преобразования Винера-Хинчина; белый шум.......................................7 3 Векторное представление сигнала; дискретизация сигнала по времени; теорема отсчетов (Котельникова); дискретизация по уровню, шум квантования; условие ретрансляции; понятие ИКМ и ДМ сигнала...............................................................14 4 Понятие информации; понятие энтропии, избыточности; оценка энтропии дискретного и непрерывного источника; энтропия шумового сигнала...................18 5 Информационная характеристика сигнала: скорость передачи сигнала; бод, скорость передачи сигнала; пропускная способность дискретного сигнала в канале с помехами; пропускная способность канала с шумовой помехой; теорема Шеннона; согласование канала с сигналом................................................................21 6 Прямое и косвенное описание процессов; некоторые модели источников сообщений; модели речевого сообщения; модели стохастического дискретного источника..........................................................................................................................26 7 Идеальный канал без помех, канал с неопределенной фазой сигнала и аддитивным шумом, канал с межсимвольной интерференцией (МСИ) и аддитивным шумом.............................................................................................................................30 8 Модели дискретного канала, модели дискретного канала с память, модель дискретно-непрерывного канала..................................................................................31 Библиографический список......................................................................................37

1 Распределение энергии в спектре периодического и непериодического сигнала; равенство Парсеваля; понятие о практической ширине частотного спектра сигнала

Сигнал – это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а целью обработки сигналов можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко – полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования.

Формы представления сигналов. Кроме привычного динамического представления сигналов и функций в виде зависимости их значений от определенных аргументов (времени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой сколь угодно сложный по своей форме сигнал, не имеющий разрывов второго рода (бесконечных значений на интервале своего задания), можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, что выполняется при помощи преобразования Фурье. Соответственно, математически разложение сигнала на гармонические составляющие описывается функциями значений амплитуд и начальных фаз колебаний по непрерывному или дискретному аргументу – частоте изменения функций на определенных интервалах аргументов их динамического представления. Совокупность амплитуд гармонических колебаний разложения называют амплитудным спектром сигнала, а совокупность начальных фаз – фазовым спектром. Оба спектра вместе образуют полный частотный спектр сигнала, который по точности математического представления тождественен динамической форме описания сигнала.

Спектральная форма представления сигнала – это представление параметров сигнала в виде двух графиков:

• спектр амплитуд;

• спектр фаз.

Спектральная диаграмма амплитуд показывает распределение энергии сигнала между составляющими его спектра. Структура спектра периодического сигнала полностью определяется значениями амплитуд и фаз гармоник. Высота линий спектра амплитуд пропорциональна амплитуде данной гармоники, поэтому их высоты различны. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники. Длины линий спектра фаз пропорциональны значению фаз. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники.

К периодическим относят гармонические и полигармонические сигналы. Для периодических сигналов выполняется общее условие s(t) = s(t + kT), где k = 1, 2, 3, ... – любое целое число, Т – период, являющийся конечным отрезком независимой переменной.

Гармонические сигналы (или синусоидальные), описываются следующими формулами:

s(t) = Asin (2πf_оt+) = Asin (ω_оt+),

s(t) = Acos(ω_оt+φ),

где А, f_o, ω_o, φ,  – постоянные величины, которые могут исполнять роль информационных параметров сигнала: А – амплитуда сигнала, f_о – циклическая частота в герцах, ω_о = 2πf_о – угловая частота в радианах, φ и  – начальные фазовые углы в радианах. Период одного колебания T = 1/f_о = 2π/ω_o. При  =  – /2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты f_о (при t = 0).

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:

s(t) =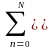 A_n sin (2πf_nt+φ_n), (1.1.2)

или непосредственно функцией s(t) = y(t  kT_p), k = 1,2,3,..., где Т_р – период одного полного колебания сигнала y(t), заданного на одном периоде. Значение f_p =1/T_p называют фундаментальной частотой колебаний. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей (f_о=0) и произвольного (в пределе – бесконечного) числа гармонических составляющих с произвольными значениями амплитуд A_n и фаз _n, с периодами, кратными периоду фундаментальной частоты f_p. Другими словами, на периоде фундаментальной частоты f_p, которая равна или кратно меньше минимальной частоты гармоник, укладывается кратное число периодов всех гармоник, что и создает периодичность повторения сигнала. Частотный спектр полигармонических сигналов дискретен, в связи с чем второе распространенное математическое представление сигналов - в виде спектров (рядов Фурье).

В качестве примера на рис. 1.1.6 приведен отрезок периодической сигнальной функции, которая получена суммированием постоянной составляющей (частота постоянной составляющей равна 0) и трех гармонических колебаний с разными значениями частоты и начальной фазы колебаний. Математическое описание сигнала задается формулой:

s(t) =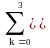 A_kcos(2πf_kt+φ_k),

где: A_k = {5, 3, 4, 7} – амплитуда гармоник; f_k = {0, 40, 80, 120} – частота в герцах; φ_k = {0, -0.4, -0.6, -0.8} – начальный фазовый угол колебаний в радианах; k = 0, 1, 2, 3. Фундаментальная частота сигнала 40 Гц. Частотное представление данного сигнала (спектр сигнала) приведено на рисунке 1.

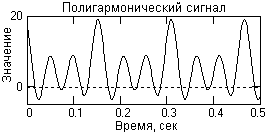
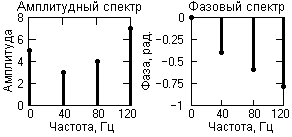
Рисунок 1 – Модель и спектр сигнала.

Периодический сигнал любой произвольной формы может быть представлен в виде суммы гармонических колебаний с частотами, кратными фундаментальной частоте колебаний f_р= 1/Т_р. Для этого достаточно разложить один период сигнала в ряд Фурье по тригонометрическим функциям синуса и косинуса с шагом по частоте, равным фундаментальной частоте f = f_p:

s(t) = 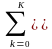(a_k cos 2πkΔft + b_k sin 2πkΔft),

a_o = (1/T)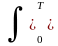 s(t) dt, a_k = (2/T) s(t) cos 2πkΔft dt,

b_k = (2/T) s(t) sin 2πkΔft dt.

Количество членов ряда Фурье K = k_max обычно ограничивается максимальными частотами f_max гармонических составляющих в сигналах так, чтобы f_max < K·f_p. Однако для сигналов с разрывами и скачками имеет место f_max   , при этом количество членов ряда ограничивается по допустимой погрешности аппроксимации функции s(t).

Одночастотные косинусные и синусные гармоники можно объединить и представить разложение в более компактной форме:

s(t) = S_k cos (2πkΔft-φ_k),

S_k =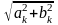 , φ_k = argtg (b_k/a_k).

Рисунок 2 – Прямоугольный периодический сигнал (меандр)

Пример представления прямоугольного периодического сигнала (меандра) в виде амплитудного ряда Фурье в частотной области приведен на рисунке 2. Сигнал четный относительно t=0, не имеет синусных гармоник, все значения φ_k для данной модели сигнала равны нулю.

К непериодическим сигналам относят почти периодические и апериодические сигналы. Основным инструментом их анализа также является частотное представление.

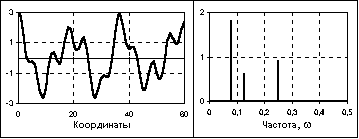
Рисунок 3 – Почти периодический сигнал и спектр его амплитуд

Почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов (в пределе – до бесконечности), но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На рисунке 4 показан пример апериодического сигнала, заданного формулой на интервале (0, ):

s(t) = exp(-at) - exp(-bt),

где a и b – константы, в данном случае a = 0.15, b = 0.17.

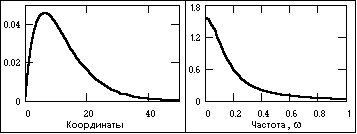
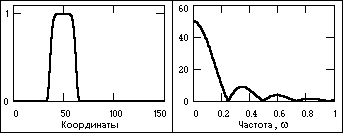
Рисунок 4 – Апериодический и импульсный сигналы и модуль их спектра

Частотный спектр апериодических сигналов непрерывен и может содержать любые гармоники в частотном интервале [0, ]. Для его вычисления используется интегральное преобразование Фурье, которое можно получить переходом от суммирования к интегрированию при Δf  0 и kΔf  f.

s(t) = (a(f) cos 2πft + b(f) sin 2πft) df = S(f) cos(2πft-φ(f)) df.

a(f) = s(t) cos 2πft dt, b(f) = s(t) sin 2πft dt,

S(f) =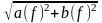 , φ(f) = argtg (b(f)/a(f)).

Частотные функции a(f), b(f) и S(f) представляют собой не амплитудные значения соответствующих гармоник на определенных частотах, а распределения спектральной плотности амплитуд этих гармоник по частотной шкале. Эти формулы обычно называют формулами прямого и обратного преобразования Фурье.

Теорема Парсеваля. Полная энергия спектра сигнала:

E_s = 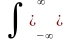W(f) df = |S(f)|² df.

Так как координатное и частотное представление по существу только разные математические отображения одного и того же сигнала, то равной должна быть и энергия сигнала в двух представлениях, откуда следует равенство Парсеваля:

|s(t)|² dt = |S(f)|² df,

т.е. энергия сигнала равна интегралу модуля его частотного спектра – сумме энергий всех частотных составляющих сигнала. Аналогично для энергии взаимодействия сигналов:

x(t) y*(t) dt = X(f) Y*(f) df.

Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:

(x(t),y(t)) = (X(f),Y(f)), ||x(t)||² = ||X(f)||².

Не следует забывать, что при представлении спектров в круговых частотах (по ω) в правой части приведенных равенств должен стоять множитель 1/2π.

Спектр частотно-модулированного сигнала. В общем виде найти этот спектр трудно. Однако для практики это и не нужно. Достаточно знать:

а) что при частотной модуляции спектр информационного сигнала 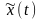переносится на несущую частоту ;

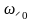б) практическую ширину спектра ЧМ-сигнала .

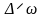Установлено, что практическая ширина спектра ЧМ-сигнала определяется выражением:

= ,

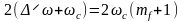где 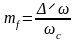– коэффициент, или индекс частотной модуляции; – девиация частоты .

При 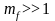имеем широкополосную ЧМ. Тогда

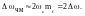
При 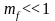имеем узкополосную ЧМ.