1. Теоретичні питання:

1.1 Охарактеризувати застосування системного аналізу в інформаційних технологіях міжнародних відносин.

1.2. Охарактеризувати множини, відношення, відображення та функції як складові моделі системи міжнародних відносин.

3. Охарактеризувати матричне обчислювання та його роль в моделюванні міжнародних відносин.

1.4. Охарактеризувати числові методи розв’язування трансцендентних рівнянь та їх роль в моделюванні міжнародних відносин.

1.5. Охарактеризувати числові методи розв’язування систем лінійних алгебраїчних рівнянь та їх роль в моделюванні міжнародних відносин.

1.6. Охарактеризувати теорію графів як апарат математичного моделювання в міжнародних відносинах.

2. Для заданого відношення навести:

а) аналітичну форму;

б) графічну форму;

в) матричну форму.

3. Для заданих матриць:

а) знайти їх суму;

б) знайти їх добуток;

в) обчислити детермінант матриці;

г) знайти обернену матрицю.

4. За заданою матрицею інцидентності :

а) побудувати граф;

б) побудувати матрицю суміжності;

в) побудувати дерево мінімальної ваги за алгоритмом Краскала;

г) побудувати дерево максимальної ваги за алгоритмом Прима;

д) побудувати маршрут мінімальної ваги з вершини e₁ до вершини e₆ за алгоритмом "гілок та границь".

Мінори та алгебраїчні доповнення.

Розглянемо визначник n-го порядку.

det A = .

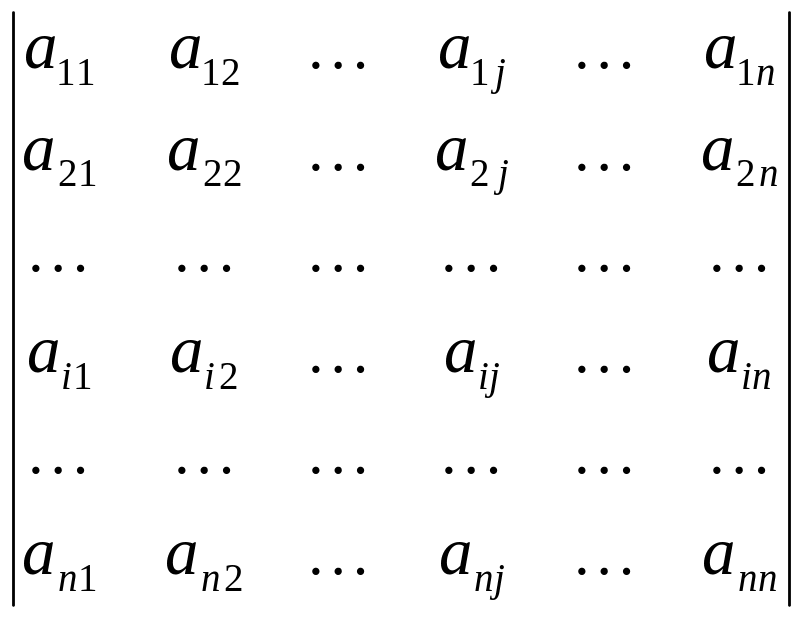Виділимо в ньому будь-який елемент а_ij. Якщо викреслити i-й рядок та j-й стовпець, на перетині яких знаходиться елемент а_ij. Отриманий визначник (n-1)-го порядку називається мінором М_ij елемента а_ij визначника _n.

Означення. Алгебраїчним доповненням A_ij елемента а_ij визначника _n називається мінор цього елемента М_ij помножений на (-!)^{i + j}, тобто величина

А_ij =(-1)^i+j М_ij.

Теорема. Розкладання визначника за i-м рядком.

Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх алгебраїчне доповнення.

Ця теорема в лінійній алгебрі називається теоремою Лапласа. Згідно з теоремою Лапласа маємо:

det A = =

= a_i1A_i1 + a_i2A_i2 + ... + a_ikA_ik + ...+ a_inA_in = .

Обчислення визначника.

I. Розкладання визначника за елементами рядка або стовпця простіше всього, коли в цьому рядку або стовпці є найбільше число нульових елементів.

Приклад.

 = .

Розкладаючи визначник третього порядку, отримуємо:

₁ =

₂ = . (тому, що третій стовпчик є лінійною

комбінацією попередніх двох).

Таким чином, отримуємо:

 = -3  (-34) + 60 = 102.

II. Розкладання визначника за елементами рядка або стовпця простіше всього, коли в цьому рядку або стовпці є єдиний не нульовий елемент.

До такого вигляду можна привести визначник шляхом операцій над його стовпцями або рядками використовуючи властивості визначника.

Процес обчислення проілюструємо наступним прикладом:

det A = =

На першому етапі намагаємося отримати якомога більше нулів в одному із стовпців або рядків. Це пояснюється тим, що після застосування формули розкладання визначників на елементи рядка (стовпця) можна отримати якнайменше число доданків.

У другому рядку визначника уже є два нулі. Отже, за основу візьмемо другий рядок. В ньому необхідно отримати більше нулів. Зауважимо, що в такому випадку дії треба виконувати над стовпцями. Таким чином, до елементів другого стовпця додамо відповідні елементи третього стовпця. Далі елементи четвертого стовпця помножимо на (-2) та додамо їх до відповідних елементів третього стовпця. Отримаємо

= .

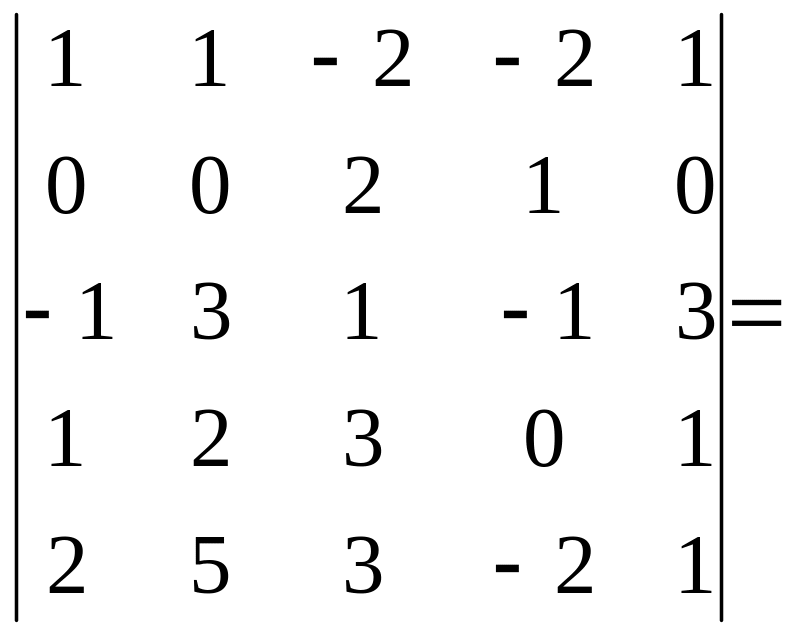
Тепер будемо розкладати визначник det A за елементами другого рядка. Отже маємо

det A = = 1 (-1)²⁺⁴  = .

Вихідний визначник знизили на один порядок. Далі знову намагаємося добитися як найбільшого числа нулів в рядку чи стовпці. Наприклад, вибираємо для зміни елементів перший рядок. Для цього помножимо на (-1) елементи четвертий стовпця та додамо їх до відповідних елементів першого стовпця.

det A = = =

Тепер елементи четвертого рядка помножимо на 4 та додамо їх до відповідних елементів другого рядка. Потім необхідно розкласти такий визначник за елементами першого стовпця.

= = 1 (-1)⁴⁺¹ =

Продовжимо зменшувати порядок визначника, для цього необхідно до елементів третього стовпця додати відповідні елементи першого. Потім елементи першого стовпця помножимо на 2 та додамо їх до відповідних елементів другого стовпця. Після перетворень розкладемо визначник за елементами першого рядка.

= = -1 (-1)¹⁺¹  =

= -1  = - (15 - 16) = - (-1) = 1.

3. Найпростіше обчислюється визначник трикутної або діагональної матриці ,він дорівнює добутку діагональних елементів. Це витікає з розкладання за елементами стовпців(рядків)визначника верхньої(нижньої) трикутної матриці (у випадку діагональної матриці розкладання можемо виконувати за елементами рядків або стовпців). Значення визначників трикутних матриць не залежить від елементів, розміщених поза головної діагоналі.

Приклади:

det B = det D =

За допомогою розкладання Лапласа можемо також показати, що визначник квазідіагональної матриці дорівнює добутку визначників квадратних матриць, розташованих по головній діагоналі:

Дійсно, розкладаючи визначник за елементами рядків матриці А₁, отримуємо єдиний ненульовий мінор, який співпадає з , і так далі.

Приклад:

IV. Схема єдиного ділення основана на послідовному перетворенні елементів визначника по провідним(опорним) елементам.

На першому кроці провідний елемент а₁₁ виноситься в якості загального множника з першого рядка, ( усі елементи першого рядка діляться на а₁₁). Потім з кожного рядка віднімається перший рядок, помножений на перший елемент даного рядка. В результаті отримаємо

a₁₁ .

Розкладаючи за елементами першого стовпця, отримуємо добуток а₁₁ на визначник (n-1)-го порядку, елементи якого виражаються співвідношенням:

Потім в одержаному визначнику вибираємо в якості провідного елемента а’₂₂ і робимо аналогічно. На k -му кроці утворюється добуток

a₁₁ a’₂₂  ... a_kk^(k-1 та визначник (n - k )-го порядку з елементами

Процедура закінчується за n - кроків.

.

Якщо на якомусь кроці = 0, то перестановкою рядків або стовпців можемо уникнути цієї ситуації.

Приклад.

5. Метод опорного елементу - це різновидність схеми єдиного ділення, який дозволяє звести визначник n -го порядку до визначника (n - 1) -го порядку, елементи якого виражені як мінори другого порядку. Нехай в якості опорного вибраний елемент a_rs. Діленням елементів r - го рядка на a_rs перетворюємо (rs) - елемент до одиниці. Далі операціями над рядками визначника, як у схемі єдиного ділення, перетворюємо усі елементи s-го стовпця, крім (rs) - елементу, в нулі. При цьому елементи визначника (за виключенням елементів r -го рядка і s -го стовпця) виражаються наступним чином:

Розкладаючи визначник за елементами s-го стовпця, отримуємо

де М_rs - додатковий мінор до (rs) - елементу, тобто визначник (n-1)-го порядку з елементами a^’_ij (i  r, j s). Кожний такий елемент є мінором другого порядку, утвореними з елементів визначника , розташованих на перетині рядків r, i і стовпців s, j. При i  r та j  s зберігається порядок елементів мінору. Для збереження такого ж порядку при r  i та s  j необхідно поміняти знаки усіх мінорів, які лежать вище r-го рядка та s - го стовпчика. Це означає, що визначник змінює знак (r-1) + (s-1) раз, що повинно бути скомпенсоване множником (-1)^r+s-2 = (-1)^r+s.

Таким чином, при збережені розположення елементів визначника

 = a_rs M_rs. Винесемо з кожного рядка M_rs загальний елемент Тоді за рахунок усіх (n - 1) рядків перед визначником (n - 1)-го порядку з’явиться множник , і в результаті отримуємо розкладання визначника  відносно опорного елемента a_rs:

Тут - визначник (n-1) - го порядку, елементами якого є мінори другого порядку. У співвідношенні з викладеним вище утворюється з  заміщенням в останньому кожного елемента a_ij (i  r, j  s) мінором, який утворений з елементів перетину рядків r ,i та стовпців s, j, зберігаючи порядок їх слідкування у початковому визначнику.

Приклад.

Для нашого прикладу виберемо а₄₁ = 1 в якості опорного елементу.

 =

В отриманому визначнику за опорний елемент приймемо а₃₃ = -1, знайдемо:

 = .