3. Наибольшее и наименьшее значения функции на отрезке.

Функция , непрерывная на отрезке [a; b], достигает своих

наибольшего и наименьшего значений либо в точках экстремума, либо на

концах отрезка. Поэтому для отыскания наибольшего и наименьшего зна-

чений функции на отрезке нужно:

1) найти критические точки функции, принадлежащие интервалу

(a; b) и ее значения в этих точках;

2) вычислить значения функции на концах отрезка, то есть найти и ;

3) из значений функции, полученных в 1) и 2) выбрать наибольшее и наименьшее число.

Пример . Найти наибольшее и наименьшее значения функции

на отрезке [−2; 2].

Решение. Найдем критические точки данной функции, принадлежа-

щие интервалу (−2; 2) и ее значения в этих точках.

; ; х₁= −1; х₂ = 3 ; у(−1) = 15.

Точка х₂ = 3 не принадлежит интервалу (−2; 2). Вычислим значения

функции на концах данного отрезка: у(−2) = 8 ; у(2) = − 12.

Сравнивая полученные результаты, имеем: у(2) = −12 – наименьшее

значение; у(−1) =15 − наибольшее значение.

4. Выпуклость и вогнутость кривой. Точки перегиба.

Определение 1. Кривая называется выпуклой на интервале

(a; b), если дуга кривой расположена ниже любой своей касательной для

этого интервала.

Определение 2. Кривая называется вогнутой на интервале

(а; b), если дуга кривой расположена выше любой своей касательной для

этого интервала.

Точки, отделяющие выпуклую часть кривой от ее вогнутой части на-

зываются точками перегиба кривой.

Теорема 1. (Достаточный признак вогнутости кривой)

Если вторая производная дважды дифференцируемой функции положительна во всех точках интервала (a; b), то кривая

вогнута на этом интервале.

Теорема 2. (Достаточный признак выпуклости кривой)

Если вторая производная дважды дифференцируемой функции отрицательна во всех точках интервала (a; b), то кривая выпукла на этом интервале.

Так как точка А(х₁; у₁) кривой отделяет выпуклую ее часть от вогнутой, то при переходе через точку х₁ производная меняет свой знак, поэтому точка х₁ является точкой экстремума производной .

Поэтому для нахождения точек перегиба кривой можно воспользоваться признаками, приведенными в 2.

Необходимый признак существования точки перегиба: если х₁ есть

абсцисса точки перегиба кривой , то либо не су-

ществует.

Значения аргумента х, при которых вторая производная равна нулю

либо не существует, называются критическими точками второго рода.

Достаточный признак существования точки перегиба: если при пе-

реходе через критическую точку второго рода вторая производная меняет свой знак, то точка является точкой перегиба кривой

.

Пример. Найти интервалы выпуклости и вогнутости и точки пере-

гиба кривой .

Решение. Дважды дифференцируем данную функцию:

; .

Определим критические точки второго рода:

3х² – 1 = 0; ; .

Точки и разбивают область определения функции на три интервала: ; ; .

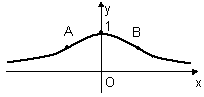
Рис. 7

В первом и третьем интервалах вторая производная положительна, поэтому исследуемая кривая на этих интервалах вогнута; на втором интервале отрицательна, а значит кривая выпукла.

Точки и есть точки перегиба графика данной функции (рис. 7).