
2. Экстремумы функции.
Определение 1.
Функция
имеет максимум
при х
= х1
(в точке х1),
если ее значение
Определение 2.
Функция
имеет минимум
при х
= х2
(в точке х2),
если ее значение
ше значений функции
во всех точках х
окрестнос-
![]() больше значений функции во всех точках
х
окрестности точки х1,
то есть
больше значений функции во всех точках
х
окрестности точки х1,
то есть
![]() (рис. 32).
(рис. 32).![]() мень-
мень-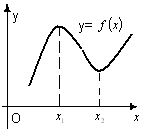
Рис.4
ти точки х2,
то есть
![]() (рис. 4)
(рис. 4)
Максимум и минимум функции называются ее экстремумами, а те
значения аргумента, при которых достигаются экстремумы функции, назы-
ваются точками ее экстремума.
Теорема 1. (Необходимое условие экстремума функции)
Если функция
имеет в точке х1
экстремум, то
![]() .
.
Точки, в которых производная функции равна нулю, называются
стационарными.
Непрерывная функция может иметь экстремум и в точках ее недиф-
ференцируемости.
Например, функция
Следовательно,
функция может иметь экстре-
мум либо в точках,
где ее производная равна нулю,
либо в точках, где
производная не существует.
Точки, в которых
производная функции равна
![]() (рис.5) в точке О имеет максимум, но не
имеет в этой точке производной.
(рис.5) в точке О имеет максимум, но не
имеет в этой точке производной.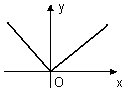
Рис. 5
нулю или не существует, называются критическими точками функции.
Теорема 2. (Первый достаточный признак экстремума функции)
Если слева от критической точки х1 функции ее производная у′ положительна (отрицательна), а справа – отрицательна (положительна),то х1 есть точка максимума (минимума) функции .
Пример
1. Исследовать
на экстремум функцию
![]() .
.
Решение. Найдем производную данной функции:
![]() .
.
Производная у′ равна нулю при х = 2; у′ не существует при х = 0. Значит, имеем две критические точки. Определим интервалы знакопостоянства производной у′ в окрестностях критических точек так же, как это делалось в примере 1.
![]()
рис. 6
При переходе через
х
= 0 производная
![]() меняет свой
знак с «плюса» на «минус», следовательно,
это есть точка максимума.
меняет свой
знак с «плюса» на «минус», следовательно,
это есть точка максимума.
При х = 2 данная функция имеет минимум.
Теорема 3. (Второй достаточный признак экстремума функции)
Если в стационарной
точке х1
вторая производная
![]() дважды диф-
дважды диф-
ференцируемой функции положительна (отрицательна), то функ-
ция имеет в точке х1 минимум (максимум).
Пример 2.
Исследовать на экстремум функцию
![]() .
.
Решение. Найдем стационарные точки данной функции:
![]() ;
;
![]() .
.
Корнями этого уравнения являются х1 = −1, х2 = 0, х3 = 1. Вторая производ-
ная у″ = 4 – 12х2. Найдем значения второй производной в каждой стацио-
нарной точке: у″ (−1) = −8 < 0 ; y″ (0) = 4 > 0 ; y″ (1) = −8 < 0.
По теореме 3 имеем: х1 = −1 и х3 = 1 являются точками максимума,
а х2 = 0 есть точка минимума данной функции.
