Задание для самостоятельной работы
Для более глубокого усвоения вопросов, связанных с понятием нормальной асимптотики пуассоновского распределения, рекомендуется решить задачи 18.573 – 18.576 из задачника [1]. Нормальная асимптотика закона хи-квадрат подробно рассмотрена в задаче 18.577. Рекомендуется также решить задачу 18.578.
3.4. Дополнительные задачи, связанные с центральной предельной теоремой
В начале приведем доказательство теоремы 3.2.1, важное в методическом отношении. Доказательство основано на применении аппарата характеристической функции, свойства которой подробно рассматривались в главе 2.
Из
условия 3) следует, что существуют
,
.Проверим,
что
- стандартизованная случайная величина.
Действительно,
,
=
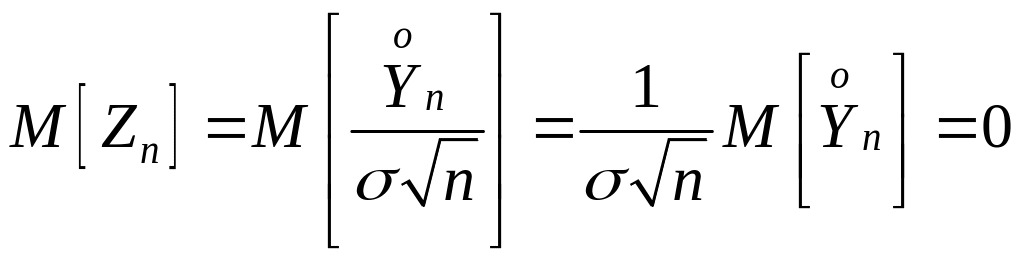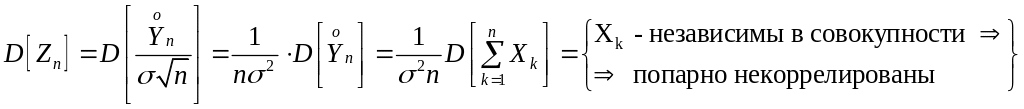Строим
характеристическую функцию
по этапам, обозначенным стрелками:
Заметим,
что по определению
.
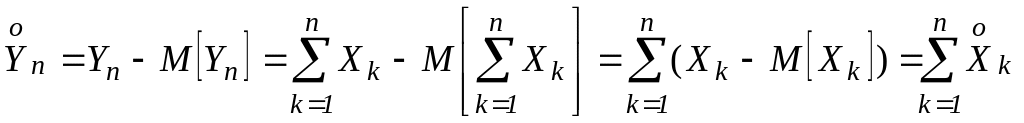I этап.
Ищем
.
Т.к. по условию 3) существует
по свойству 4) характеристической функции
существует
и
.
Разложим функцию
в ряд Тейлора до членов второго порядка
включительно с остаточным членом в
форме Пеано
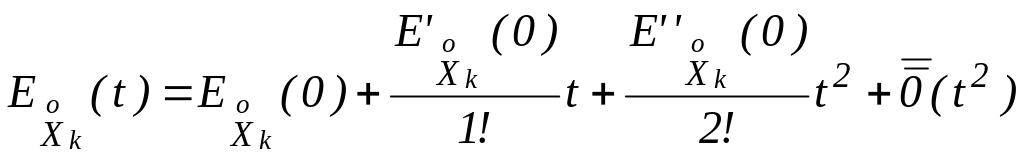; (3.4.1)
(по
свойству 2 характеристической функции).
Далее по свойству 3 характеристической функции
;
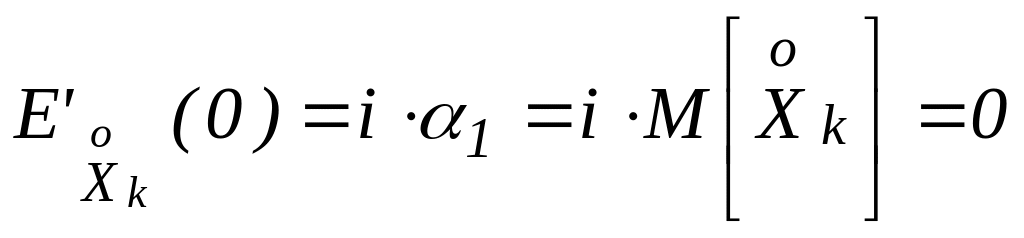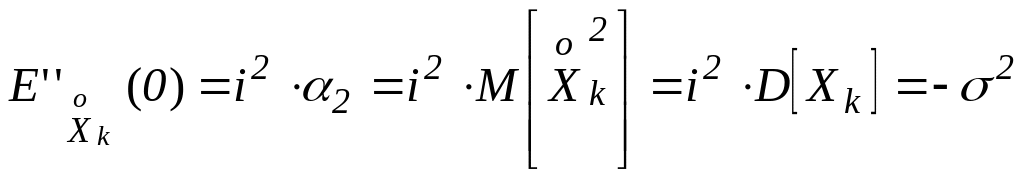
Подставим полученные значения производных в (3.4.1):
(3.4.2)
II
этап.
Так как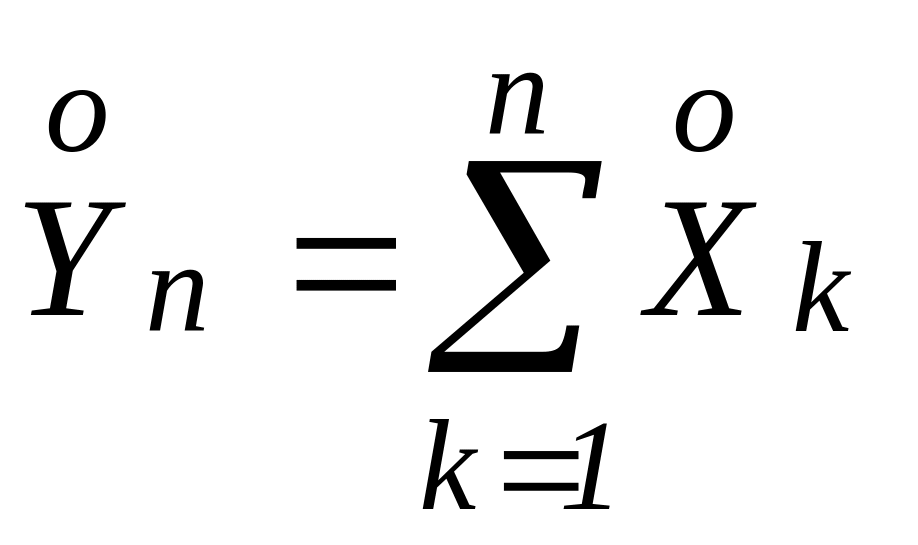
{по свойству 5 характеристической
функции}
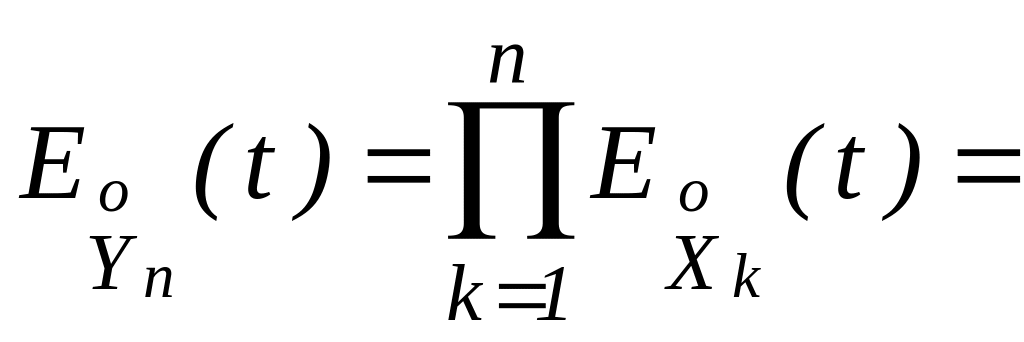{подставляем
(3.4.2)} =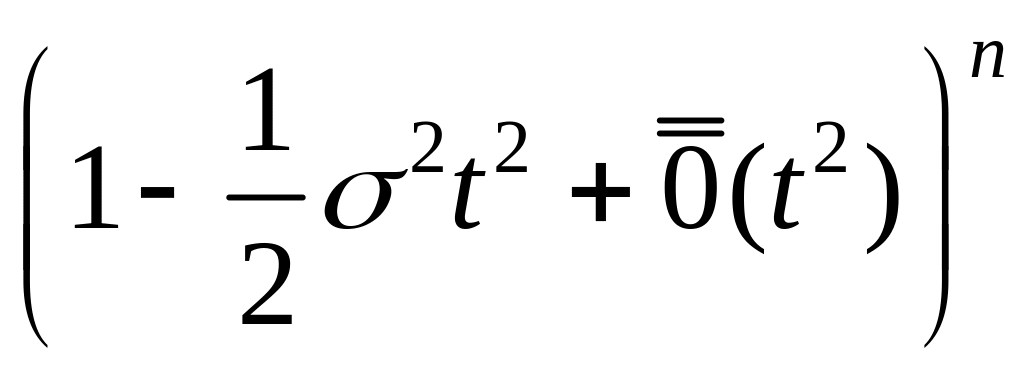
III
этап.
{
по свойству 4 характеристической функции}
=
=
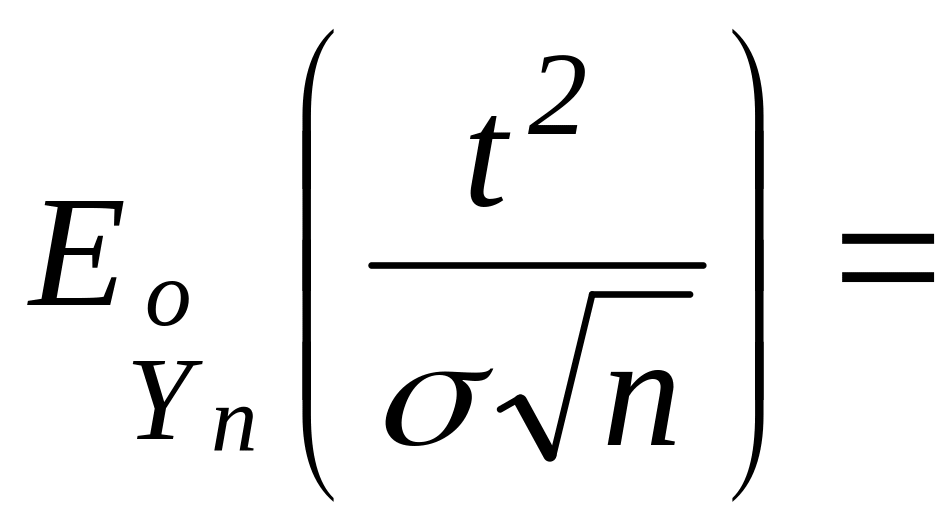
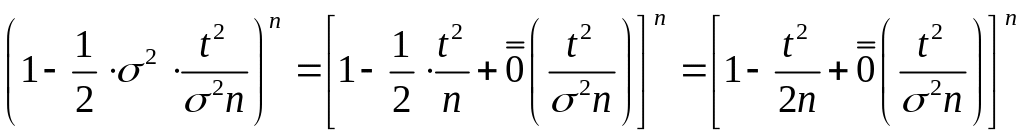
Итак,
.
=
={
,
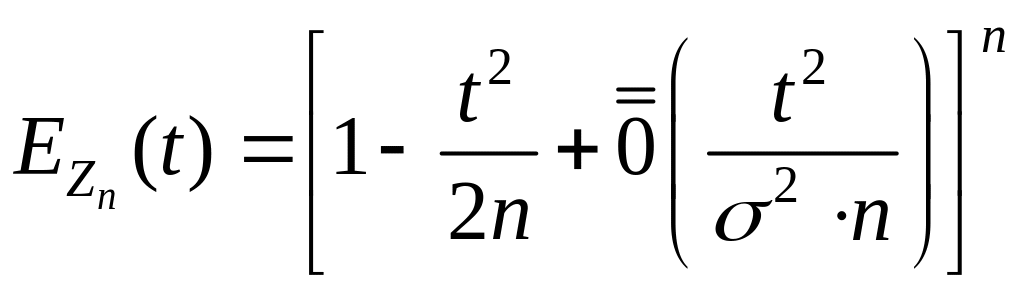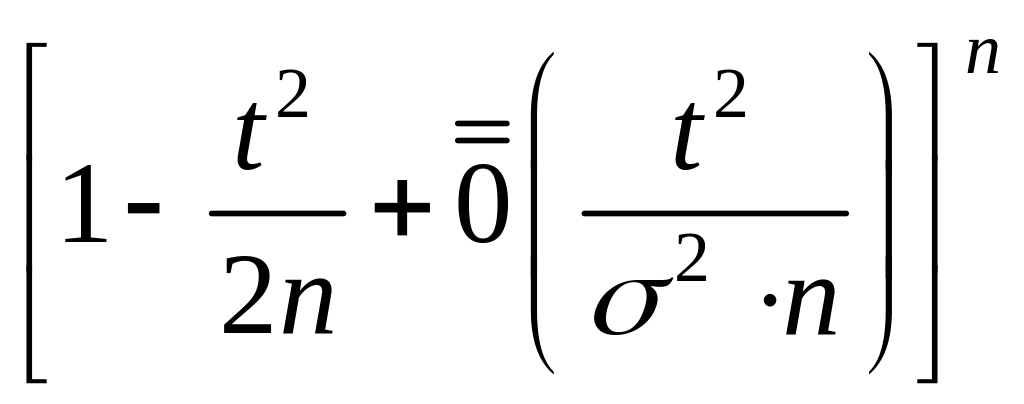- малое} =
=
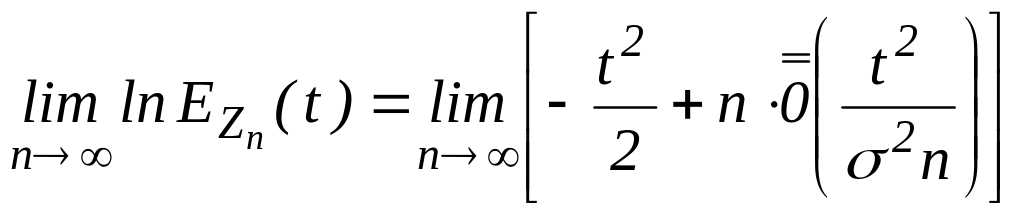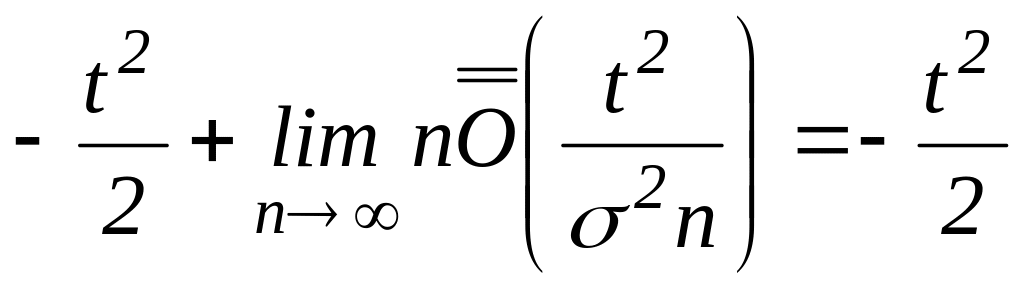
Обратимся теперь к более тонкому и сложному вопросу об оценке погрешности нормального приближения в интегральной теореме Муавра-Лапласа. Ранее уже говорилось, что точной формулы для указанной погрешности не существует. Однако оказывается, что можно получить оценку для так называемой предельной абсолютной погрешности для любого промежутка.
Современные
исследования по уточнению ЦПТ для
конечных n
приводят к следующему результату.
Оставаясь в рамках формулировки ЦПТ,
данной нами выше (теорема 3.2.1 для одинаково
распределенных слагаемых) и сохраняя
введенные там обозначения, потребуем
дополнительно существования у членов
последовательности
третьего абсолютного момента. Обозначим
.Тогда
справедливо следующее неравенство
(известное в литературе как неравенство
Берри-Эссена [4]):
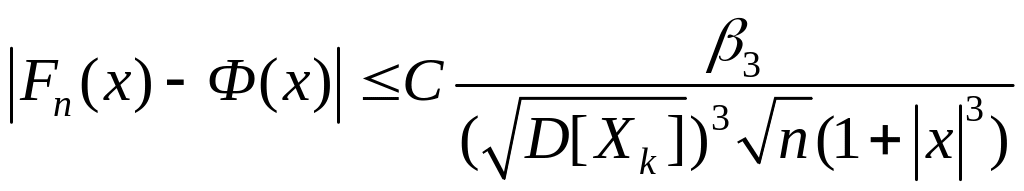, (3.4.3)
где
- точная функция распределения для
стандартизованной суммы, а
- некоторая абсолютная константа, которая
последовательно уточнялась в работах
главным обоазом российских математиков,
и удовлетворяет неравенству
(3.4.4)
Неравенства (3.4.3) и (3.4.4) позволяют установить величину предельной абсолютной ошибки, допускаемой при использовании интегральной теоремы Муавра-Лапласа.
Пример
3.4.1.
Пусть
подчиняется закону
,
.
Обозначим
,
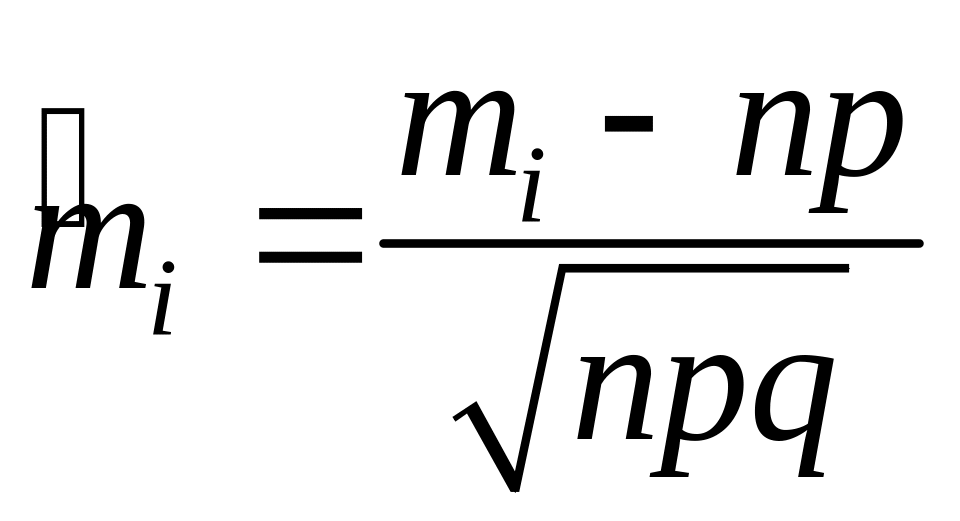=1,2;
-
точное
значение искомой вероятности попадания
биномиальной случайной величины на
промежуток
;
- приближенное значение той же вероятности,
вычисленное в предположении нормальности
.
Показать, что справедлива следующая
оценка:
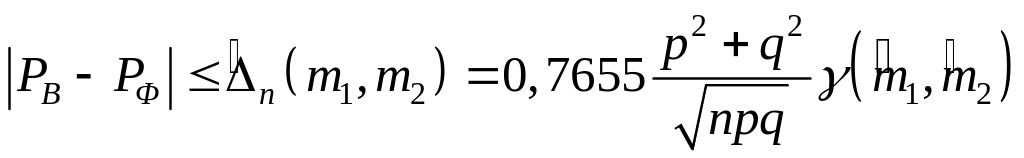(3.4.5)
где
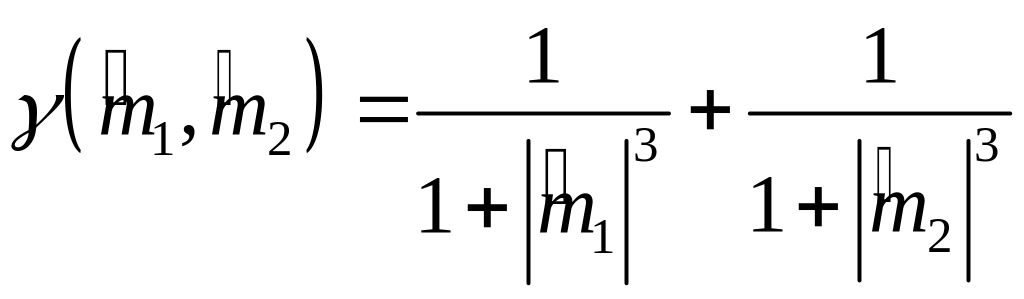
◄ Воспользуемся
представлением
,
где
- индикатор успеха в
-м
опыте, причем для последовательности
выполняются все условия ЦПТ. ►
Используя
закон распределения индикатора
:
находим:
,
Подставляя полученные характеристики в правую часть неравенства (3.4.1) и учитывая (3.4.2), получаем:
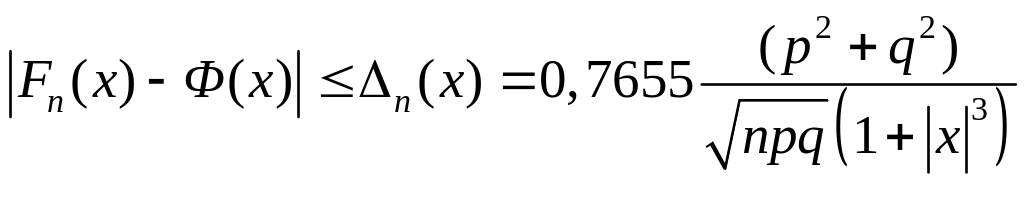(3.4.6)
Используя свойства модуля, распишем левую часть часть в (3.4.6):
,
где
определяется формулой (3.4.6). Обозначая
,
получаем требуемый результат (3.4.5).►
Полученная
в примере величина
имеет смысл предельной абсолютной
погрешности нормальной аппроксимации
биномиальной вероятности попадания на
промежуток
.
Она дает лишь грубую оценку сверху для
абсолютной погрешности нормального
приближения при достаточно больших
значениях
и используется на практике для получения
гарантированных оценок (истинная
величина абсолютной ошибки всегда
меньше полученной предельной ошибки).
Пример 3.4.2. В условиях примера 3.3.7 вычислить предельные абсолютную и относительную погрешности нормального приближения для указанных промежутков.
◄ а) Для
промежутка [15,35]
вычислим нормированные значения концов
интервала:
=
=
,
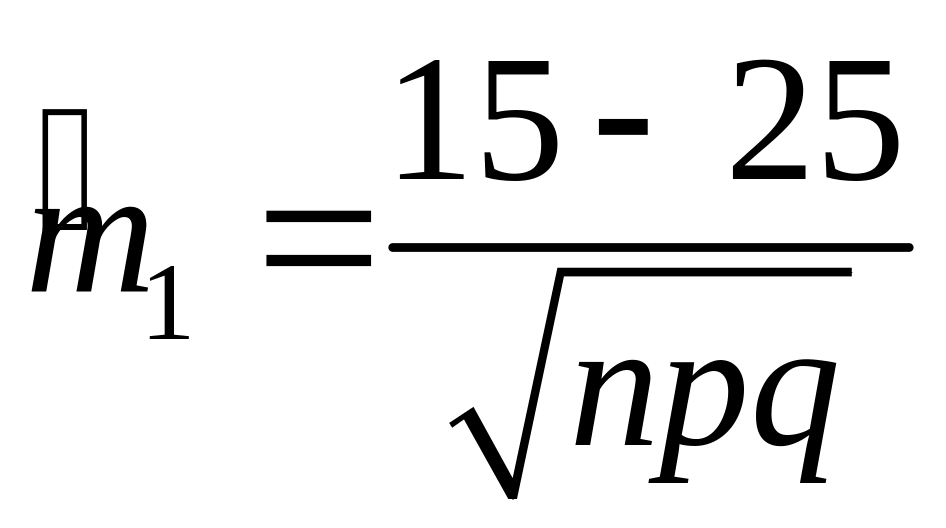2,3095;
Отсюда следует:
0,15;
Далее по формуле (3.4.5) получаем:
0,7655
=0,01657.
Учитывая
точное значение
=0,9852,
взятое из таблицы 3.3.2, получаем предельную
относительную ошибку для данного
промежутка
1,68%,
в то время как истинное значение
относительной ошибки, указанное в той
же таблице равно 0,62%.►
б)
Промежуток [20,30].
Ответ: 0,087;
=18,39%.
в) Промежуток
[30,40]. Ответ:
=0,417;
=0,046;
=30,88%.
Пример 3.4.3.
Вероятность выпуска микросхемы с
дефектом равна 0,03. На контроль поступила
партия из 2000 микросхем. Пусть
- число дефектных микросхем в данной
партии. Вычисляется вероятность события
с помощью интегральной теоремы
Муавра-Лапласа. Какую предельную
абсолютную (и относительную) ошибку мы
при этом допускаем?
◄ По условиям данного эксперимента =0,03, =2000, =60, =7,6289. (все вычисления проводятся с 4 верными знаками после запятой). Преобразуя неравенство под знаком к неравенству для стандартизованной случайной величины , получаем:
.
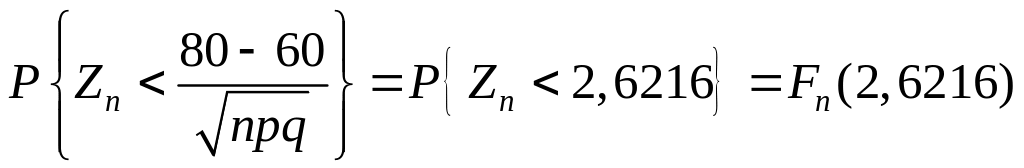Далее по формуле
(3.4.6) при
=2,6216
находим:
=0,0052.
Так как точное
значение искомой вероятности неизвестно,
то для предельной относительной
погрешности используем формулу
,
где
=0,9956
– приближенное значение. Таким образом,
получаем
=0,0052
или 0,52%, что в данном случае является
вполне приемлемой гарантированной
точностью.►
Пример 3.4.4.
В условиях предыдущего примера вычислить
предельные абсолютную и относительную
ошибки для вероятности события
.
Ответ: =0,036; =3,38%.
Пример 3.4.5.
Каково гарантированное число опытов,
которые необходимо провести по схеме
Бернулли с вероятностью успеха в одном
опыте
=1/2,
чтобы предельная абсолютная погрешность
нормального приближения для вероятности
события
не превосходила 0,01? Рассмотреть два
случая:
1)
;
2)
.
◄ 1) Преобразуем
=
.
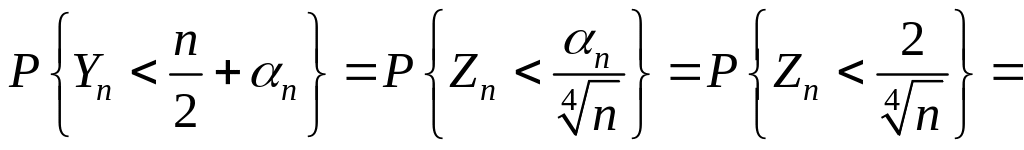
Полагая в формуле (3.4.6)
,
получаем, согласно условию,
.
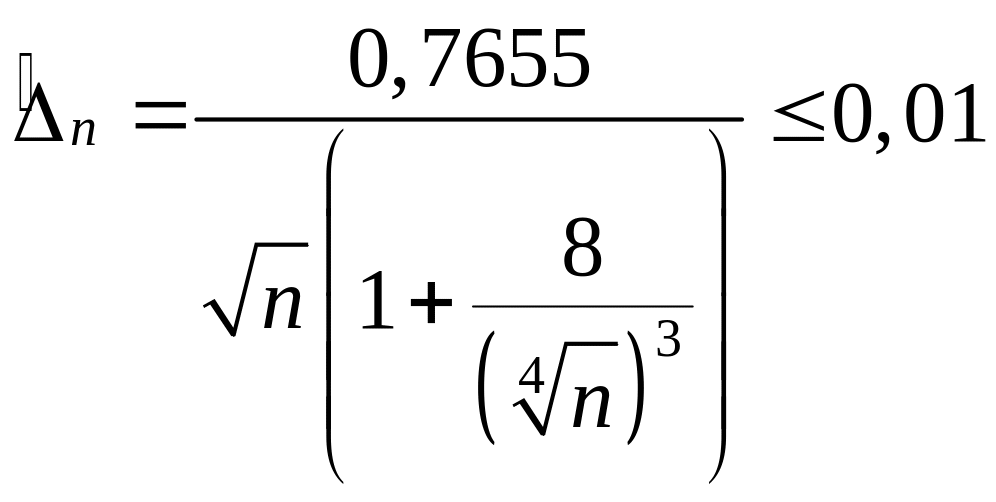Учитывая, что
и отбрасывая в первом приближении малое
слагаемое в знаменателе дроби, получаем
5860.►
2) Ответ:
.
Пример 3.4.6.
Случайные величины
независимы и имеют одно и тоже
геометрическое распределение с параметром
=1/2.
Показать, что
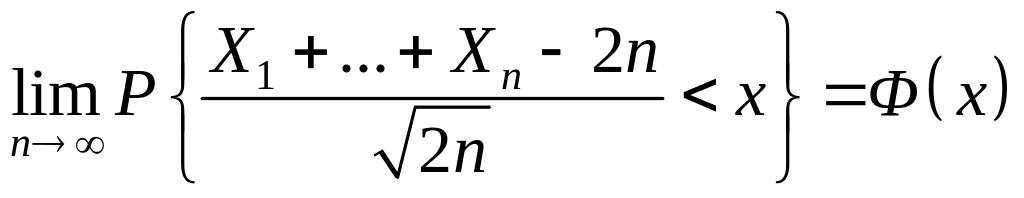. (3.4.7)
◄ Так как для геометрического распределения справедливы формулы:
,
,
то согласно свойствам мат.ожидания и
дисперсии, имеем:
,
.
Таким образом, для последовательности
выполнены все условия ЦПТ. Следовательно
предельным законом распределения для
стандартизованной суммы
при
будет нормальный
.
Данное утверждение формулируется в
терминах функции распределения в виде
равенства (3.4.7).►