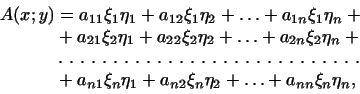4 Билинейные и квадратичные формы

В этом параграфе мы будем опять заниматься аффинным пространством, а именно, будем изучать простейшие числовые функции от векторов в аффинном пространстве.

1 Линейная функция.

Простейшей функцией в аффинном пространстве является линейная функция.

Определение 4.1   Говорят, что в аффинном пространстве задана линейная функция (линейная форма), если каждому вектору   поставлено в соответствие число  , так что при этом выполнены условия:

1   .

2   .

Выберем в  -мерном пространстве произвольный базис  . Так как каждый вектор   можно представить в виде

то в силу свойств линейной функции имеем:

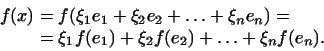
Итак: в  -мерном пространстве с заданным базисом линейная функция может быть представлена в виде

(1)

где   -- постоянные, зависящие лишь от выбора базиса, а   -- координаты вектора в этом базисе.

Таким образом, данное выше определение линейной функции совпадает, по существу, с принятым в алгебре определением линейной функции (линейной формы); надо лишь иметь в виду, что в нашем случае коэффициенты зависят от выбора базиса.

Выясним, как меняются коэффициенты линейной функции при замене одного базиса другим.

Пусть   и   -- два базиса в  . Пусть, далее, векторы   выражаются через базис   формулами

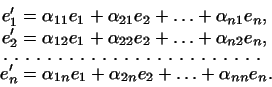
Пусть в базисе   линейная функция выражается формулой

а в базисе   -- формулой

Так как  , а  , то

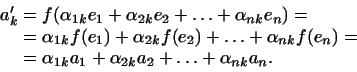
Мы видим, следовательно, что коэффициенты линейной формы преобразуются при переходе к другому базису так же, как векторы базиса (или, как иногда говорят, когредиентно векторам базиса).

Пример 1   1. В пространстве, векторами которого являются непрерывные функции  , заданные на отрезке  , рассмотрим функцию  , заданную формулой

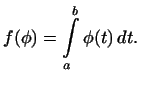
Эта функция линейна, так как выполняются условия 1  и 2 .

Действительно, первое из них означает, что интеграл суммы равен сумме интегралов, а второе означает, что постоянный множитель можно выносить за знак интеграла.

Пример 2   2. В том же пространстве рассмотрим функцию  , определенную следующим образом. Выберем на отрезке   некоторое значение   и положим

Проверьте, что эта функция   также линейна.

2 Билинейные формы.

Существенную роль в дальнейшем будут играть билинейные и квадратичные функции (формы).

Определение 4.2   Мы говорим, что   есть билинейная функция (билинейная форма) от векторов   и  , если:

1  при фиксированном     есть линейная функция от  ,

2  при фиксированном     есть линейная функция от  .

Иными словами, в силу определения линейной функции условия 1  и 2  означают соответственно

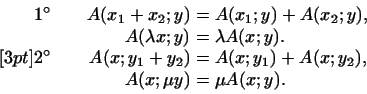
Примеры   1. Рассмотрим  -мерное пространство, в котором вектор есть совокупность   чисел. Положим

где   есть вектор  , а   -- вектор  . Формула (2) определяет билинейную функцию. В самом деле, если зафиксировать  , т.е. считать   постоянными, то 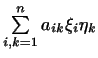 зависит от   линейно, т.е. есть линейная функция от  , а при постоянных   форма   -- линейная функция от  .

2. В пространстве, в котором векторами являются непрерывные функции  , рассмотрим следующий пример билинейной функции. Пусть   -- некоторая непрерывная функция переменных   и  . Положим

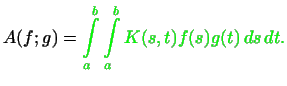
 есть билинейная функция векторов   и  .

Действительно, условия 1  и 2  проверяются так же, как и в примере 1 предыдущего пункта.

Если  , то

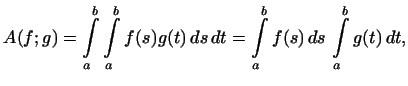
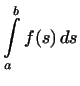т.е.   есть произведение линейных функций   и  .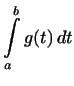

Упражнение   Показать, что если   и   -- линейные функции, то их произведение   есть билинейная функция.

Определение 4.3   Билинейная функция (форма) называется симметрической, если для любых векторов   и   имеет место равенство

В приведенном выше примере 1 определенная формулой (2) билинейная форма   симметрична тогда и только тогда, когда   для любых   и  .

Скалярное произведение   в евклидовом пространстве является примером симметрической билинейной формы.

В самом деле, аксиомы 1 , 2 , 3  скалярного произведения ( 2) как раз и означают, что скалярное произведение есть симметрическая билинейная форма.