6. Помехоустойчивое (канальное) кодирование

6.1. Общие свойства линейных блоковых кодов

Блоковый код состоит из векторов длины - кодовых слов (см. п. 1.2). В каждом векторе разрядов – информационные ( ), остальные - проверочные. Если - основание кода, полное число кодовых слов , число разрешенных кодовых слов - . Скорость кода равна . Сложение кодовых слов по описано в п. 1.1. Сумма по любой пары кодовых слов - кодовое слово того же кода (свойство замкнутости линейного кода). Среди кодовых слов есть нулевое.

Каждый двоичный код характеризуется распределением весов кодовых слов (см. п. 1.2). Оно позволяет найти расстояния Хэмминга между любыми его кодовыми словами. По свойству замкнутости, для любой пары ненулевых слов кода расстояние между ними равно весу какого-то другого ненулевого слова того же кода. Значит, кодовое расстояние равно минимальному весу, возможному для ненулевого слова кода.

Пусть - вектор информационных символов на входе кодера. Строки порождающей матрицы размерности образуют базис из линейно независимых векторов в -мерном пространстве. Кодовое слово на выходе кодера

(6.1)

Каждый выбор порождает свой код. Любую из этих матриц операциями над строками и перестановкой столбцов можно привести к канонической форме: , где - единичная матрица размерности , - матрица (размерности ) проверочных (избыточных) символов. Матрица канонической формы дает систематический код. В каждом его кодовом слове первые разрядов содержат информационные символы, а остальные разрядов – проверочные. Порождающие матрицы, преобразуемые друг в друга линейными операциями над строками и перемещением столбцов, эквивалентны и производят эквивалентные коды.

Кодер систематического двоичного кода строят, используя регистр сдвига на бит, сумматоров по , связанных с ячейками регистра и образующих проверочные символы. Последние заносятся во ой регистр сдвига длины . Затем информационных битов, а за ними - проверочных, последовательно идут из регистров на модулятор.

Пример 6.1.1. У систематического кода с порождающей матрицей

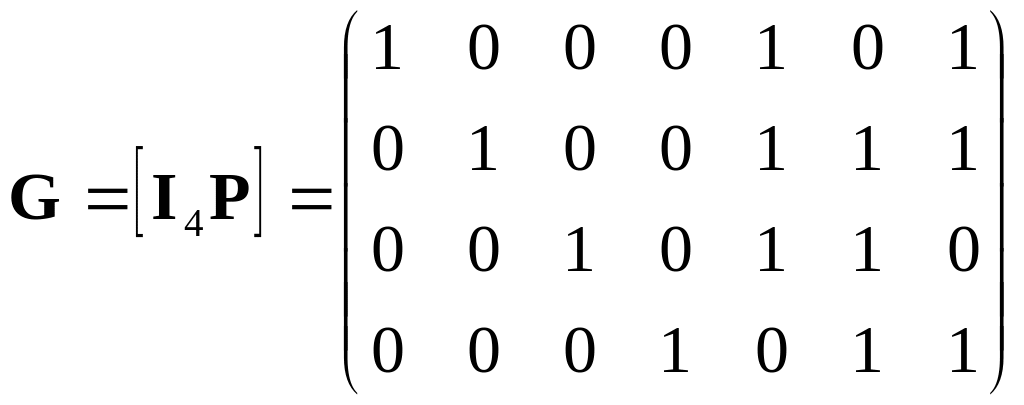
кодовое слово - , где - информационных бита, - проверочных бита, и Кодер для этого кода показан на рис. 6.1.

Рис. 6.1 Схема кодера блокового линейного кода

Для любого линейного кода существует дуальный (двойственный) код . Любое кодовое слово кода ортогонально любому кодовому слову дуального кода. Порождающая матрица размерности дуального кода имеет линейно независимых векторов-строк, причем

, (6.2)

где - вектор-столбец из нулей. В частности, , где - матрица из нулей размерности . Для систематического кода с порождающей матрицей дуальный код имеет порождающую матрицу

, (6.3)

где для двоичного кода знак минус можно опустить, так как вычитание по идентично сложению по . Подставив (6.3) в (6.2), найдем уравнения проверки

(6.4)

где , - элементы канонической матрицы , образующие матрицу , - ый элемент кодового слова .

В (6.4) проверочные символы кодовых слов образованы разными линейными комбинациями информационных символов. Матрицу называют также проверочной матрицей кода . Она позволяет построить код с заданным кодовым расстоянием, согласно следующей теореме.

Теорема о построении блокового кода. Кодовое расстояние линейного кода равно тогда и только тогда, когда любые столбцов проверочной матрицы этого кода линейно независимы, но некоторые столбцов проверочной матрицы линейно зависимы.

Декодирование сводится к нахождению синдрома - вектора размерности :

(6.5)

где - вектор принятого кодового слова. Только если последнее совпадает с одним из разрешенных (нет ошибок в принятых символах или из-за помех одно разрешенное слово перешло в другое), . Тогда декодер решает, что ошибок нет. С учетом (1.5) и (6.5) выразим синдром через вектор ошибок : , где - вектор переданного кодового слова. Число разных синдромов для разных сочетаний ошибок равно . По виду синдрома в пределах корректирующей способности кода можно найти и исправить ошибочные символы.

Декодер линейного кода состоит из разрядного сдвигающего регистра, блоков сумматоров по , схемы сравнения, анализатора ошибок и корректора. Регистр нужен для запоминания информационных символов принятого кодового слова. Из них в блоках сумматоров, согласно (6.4), образуются проверочные символы. Анализатор ошибок по виду синдрома, получаемого сравнением формируемых на приемной стороне и принятых проверочных символов, находит места ошибочных символов. Ошибки исправляет корректор. При декодировании линейного кода с исправлением ошибок в памяти декодера надо, вообще говоря, хранить таблицу соответствий между синдромами и векторами ошибок, содержащую строк. Схема декодера линейного кода показана на рис. 6.2.

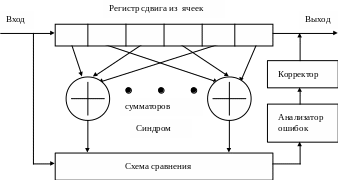
Рис. 6.2. Структурная схема декодера блокового линейного кода

При независимых ошибках в канале корректирующая способность кода выражается через кодовое расстояние . Пусть есть двоичный код с . Искажение го символа меняет расстояние Хэмминга на . Значит, код с обнаруживает не все одиночные ошибки. Для обнаружения любой одиночной ошибки надо иметь . Рассуждая аналогично, найдем, что для обнаружения всех ошибок кратности нужен код с .

В двоичном коде с расстоянием есть хотя бы два кодовых слова и , различные в символах. Для них можно найти два вектора ошибок и с числом единиц , переводящих и в одно и то же запрещенное слово . Любое запрещенное слово входит лишь в одно из подмножеств , (см. п. 1.4). Тогда код может не исправить хотя бы одну ошибку кратности . Код исправит все ошибки кратности , если . Аналогично найдем, что если код исправляет ошибки кратности и обнаруживает ошибки кратности , то .

Кроме режима декодирования с обнаружением и исправлением ошибок, есть режим с восстановлением предварительно стертых ненадежных символов (см. п. 1.5). Решение о переданном символе принимается, если входной сигнал не попадает в область неопределенности решающей схемы приемника. Иначе этот символ заменяется символом стирания. Стертые символы восстанавливают корректирующими кодами. Кодовое расстояние связано с числом восстанавливаемых символов. Если в принятом слове стерто символов, остальные приняты верно. Из принятых слов образуем укороченные (без стертых символов). Для принятия решения по последним надо, чтобы они различались хоть в ом символе. Полные слова могут отличаться еще в позициях. Значит, для восстановления стертых символов нужно кодовое расстояние . Это совпадает с условием обнаружения ошибок кратности . Восстановить стертые символы проще, чем исправить ошибочные: разряды х известны, а х - нет.

Получение кода с заданной корректирующей способностью сведено нами к обеспечению необходимого кодового расстояния путем введения избыточности. Желательно, чтобы число проверочных символов было минимально. Есть ряд оценок максимального кодового расстояния при заданных и , полезных для определения степени близости построенного кода к оптимальному. Можно показать , что если есть блоковый линейный двоичный код , для него справедлива верхняя граница Хэмминга:

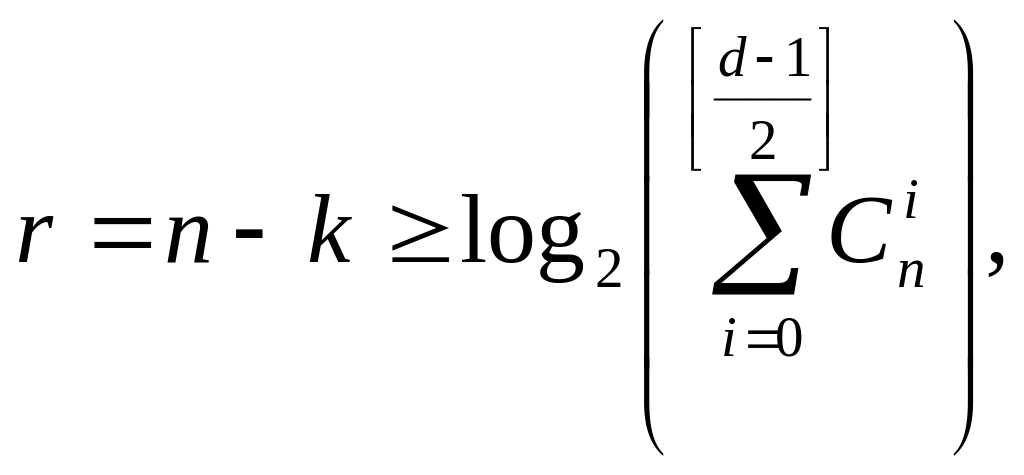(6.6)

где - целая часть числа . Граница Хэмминга (6.6) близка к оптимальной для кодов с большими значениями скорости . Для кодов с малыми значениями более точна верхняя граница Плоткина

(6.7)

Можно показать, что есть блоковый линейный код с кодовым расстоянием , для которого справедлива нижняя граница Варшамова-Гильберта

(6.8)

Границы Хэмминга и Плоткина дают необходимые условия существования двоичного кода, а граница Варшамова-Гильберта - достаточные. Границы (6.6) - (6.8) обобщаются на недвоичные коды, а (6.7) – и на нелинейные. В (6.6) равенство верно лишь для совершенных кодов. Они исправляют все ошибки кратности , но не исправляют ни одной ошибки большей кратности. Число известных совершенных кодов мало. Например, - это коды Хэмминга (см. п. 6.2). Равенство в (6.7) верно лишь для эквидистантных кодов. Например, - для кодов Адамара (см. п. 6.3).

Пример 6.1.2. Оценим близость к оптимальному БЧХ-кода с . Из (6.6) находим , а из (6.8) - . То есть, нет кодов длиной с и , но есть коды длиной с и . Изучаемый код имеет и является достаточно хорошим.