
- •Лекция 1
- •Принятые обозначения и символика
- •Требования, предъявляемые к чертежу:
- •Сущность операции проецирования
- •Виды проецирования
- •Центральное проецирование
- •Параллельное проецирование
- •Общие свойства проецирования
- •Ортогональные проекции (прямоугольные проекции или мет. Монжа)
- •Частные случаи расположения т-ек в пространстве
- •Построение дополнительной профильной плоскости пр-ий
- •Лекция 2 Линии. Изображение линии на эпюре Монжа.
- •Определитель линии
- •Изображение прямой общего положения на эпюре.
- •Прямые частного положения.
- •Принадлежность т-ки линии.
- •Следы прямой линии.
- •Взаимное расположение прямых линий.
- •Определение видимости геометрических элементов.
- •Теорема о прямом угле.
- •Лекция 3 Плоскость
- •Следы плоскости.
- •Признак принадлежности т-ки и прямой пл-ти.
- •Главные линии пл-ти (особые)
- •Лекция 4 Преобразование чертежа.
- •Перемена плоскостей проекций.
- •Замена фронтальной плоскости проекций.
- •Замена горизонтальной плоскости проекций.
- •Определение истинной длины отрезка прямой методом прямоугольного треугольника.
- •Лекция 5 Способ вращения.
- •Вращение вокруг линии уровня.
- •Лекция 6 Поверхности
- •Линейчатые поверхности.
- •Линейчатые поверхности с одной направляющей
- •2. Поверхности, образованные 2-мя направляющими и пл-тью параллелизма
- •Принадлежность т-ки поверхности.
- •Винтовые поверхности.
- •Лекция 7 Поверхности вращения (ротационные).
- •1 Гр. Поверхности, образованные вращением плоской кривой.
- •Принадлежность т-ки поверхности.
- •2 Гр. Поверхности, образованные вращением прямой.
- •3 Гр. Поверхности, образованные вращением окружности.
- •4 Гр. Поверхности, образованные вращением кривых II порядка.
- •Лекция 8 Пересечение поверхностей.
- •Свойство проецирующей поверхности:
- •Частные случаи пересечения поверхностей.
- •Обе пересекающиеся поверхности – проецирующие.
- •Одна из пересекающихся поверхностей – проецирующая.
- •Конические сечения
- •Лекция 9 Общий случай пересечения поверхностей.
- •Лекция 10 Пересечение прямой с поверхностью или плоскостью (основная задача нг)
- •Развёртки поверхностей.
- •Свойства взаимооднозначного соответствия:
- •Развёртки гранных поверхностей.
- •Развёртка пирамиды.
- •Развёртка призмы.
- •Лекция 11 Развёртки кривых поверхностей.
- •1. Развёртка прямого кругового конуса.
- •2. Развёртка прямого кругового цилиндра.
- •Развёртка сферы и тора.
- •Лекция 12 Проекции с числовыми отметками.
- •Изображение прямой.
- •Заложение, превышение, интервал и уклон прямой.
- •Градуирование прямой.
- •Прямые частного положения
- •Взаимное расположение прямых
- •Изображение плоскости.
- •Лекция 13 Взаимное расположение плоскостей
- •Взаимное расположение прямой и плоскости Пересечение прямой с пл-тью
- •Перпендикулярность прямой и плоскости
- •Изображение поверхностей
- •Поверхность одинакового ската (равного уклона) (не надо)
- •Топографическая поверхность
- •Построение линии наибольшего ската топографической пов-сти
- •Лекция 14 Определение границ земляных работ
Принадлежность т-ки линии.

Теорема : Т-ка принадлежит линии, если одноимённые пр-ии т-ки лежат на одноимённых пр-ях линии.
Следы прямой линии.
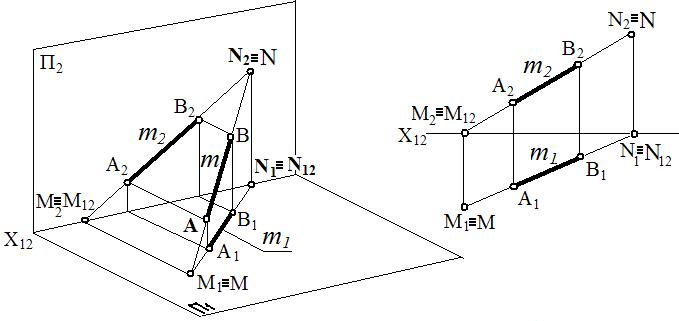
Определитель прямой m задаётся 2-мя т-ми: m (А, В).
m является прямой общего положения, т.е. произвольно наклонена к плоскостям пр- ий.
На прямой имеются характерные т-ки, т.е. следы прямой.
След прямой – это точка, в которой прямая пересекается с плоскостью пр-ий.
Прямая m пересекается с П1 – получаем горизонт. след прямой М, и соответственно, пересечение прямой m с фронт. пл-тью пр-ий дает нам фронт. след прямой – N.
Фронтальная пр-ия N совпадает с N2 , горизонт. пр-ия совпадает с N12. И, соответственно М ≡ М1 , М2 ≡ М12.
Взаимное расположение прямых линий.
Прямые в пространстве могут:
быть параллельными;
пересекаться;
скрещиваться.
Д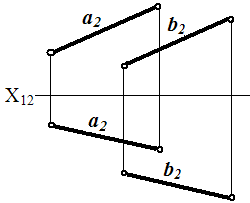 ве
прямые a и b
|| в простр-ве, если
ве
прямые a и b
|| в простр-ве, если
они пересекаются в бесконечно
удалённой т-ке (в несобственной).
На черт. одноимённые пр-ии параллельных
прямых так же параллельны.
с и d пересекаются в простр-ве (с ∩ d)
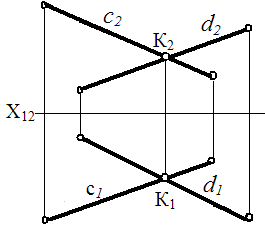 на черт.: с1 ∩ d1
К1
на черт.: с1 ∩ d1
К1
с2 ∩ d2 К2
К – пр-ия т-ки пересечения с и d
К1 К2 Х12
Прямые пересекаются, если их одноимённые проекции также пересекаются, а проекции т-ки пересечения лежат на одной линии связи.
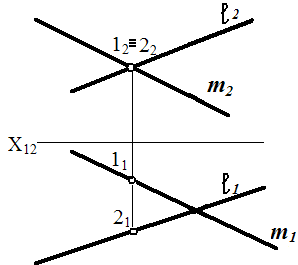
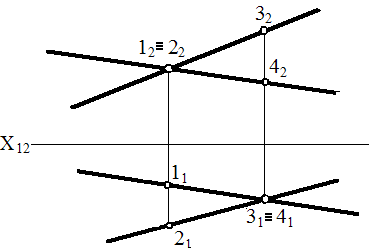
ℓ и m – скрещивающиеся прямые, т.к.
ℓ 2 ∩ m2 т12 ≡ 22 ,
а 11 и 21 – отдельные пр-ии.
Прямые скрещиваются, если они не
пересекаются и не ||-ны между собой,
а т-ки пересечения их одноимённых
проекций не лежат на одной линии связи.
Определение видимости геометрических элементов.
Положение скрещивающихся прямых положено в основу метода конкурирующих точек, который используется для определения видимости поверхностей:
Видимость на горизонт. пр-ии определяется по фронтальной: видима та т-ка, которая расположена выше (больше высота).
В
 идимость
на фронт. пр-ии определяется по горизонт:
видима та т-ка, которая расположена
дальше от оси Х (больше глубина).
идимость
на фронт. пр-ии определяется по горизонт:
видима та т-ка, которая расположена
дальше от оси Х (больше глубина).
Теорема о прямом угле.
Если одна сторона прямого угла параллельна какой-либо плоскости пр-ий, а другая сторона не перпендикулярна к ней, то на эту плоскость пр-ий прямой угол проецируется в НВ.
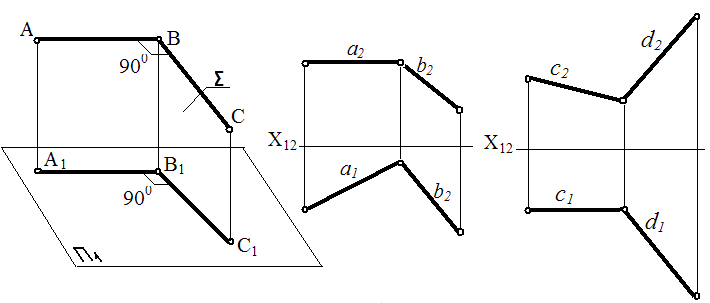
Если две прямые пересекаются под прямым углом, то проекции их в общем случае образуют угол, не равный 900.
Для того, чтобы прямой угол проецировался в НВ, необходимо и достаточно, чтобы одна из его сторон была ||-на, а другая не -на пл-ти пр-ий.
Действительно, пусть сторона АВ прямого угла АВС ||-на пл-ти П1. требуется доказать, что проекция его: угол А1В1С1 = 900.
Прямая АВ -на пл-ти ∑, т.к. АВ -на двум прямым этой пл-ти ВС и ВВ1, проходящим через т-ку В.
Прямая АВ и её пр-ия А1В1 – две ||-ые прямые, а потому А1В1 также -на пл-ти ∑. Следовательно, А1В1 -на В1С1.
На основании изложенного, можно утверждать, что углы, показанные на рис 2 и 3, являются проекциями прямых углов. На рис. 2 сторона a ||-на пл-ти П1, а на рис.3 – сторона с ||-на пл-ти П2.
