4.Системы линейных уравнений Метод матричный.

Матричный метод решения СЛУ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными [2]:

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

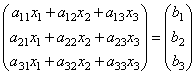
или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т. к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A:.

Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A^-1B.

5.Системы линейных уравнений Метод Гаусса.

Метод Гаусса (метод последовательного исключения)

Наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.

Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений [1].

Рассмотрим систему из трёх уравнений с тремя неизвестными:

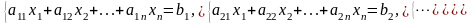(5)

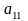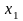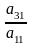Для определенности положим, что коэффициент отличен от нуля. Если это не так, то поменяем строки местами или сделаем перенумерацию переменных. Преобразуем систему (5), исключая переменную из всех уравнений, кроме первого. Для этого обе части первого уравнения умножим на и вычтем из соответствующих частей второго уравнения, затем обе части первого уравнения умножим на и вычтем из соответствующих частей третьего уравнения и т.д. В результате придем к новой СЛУ с n неизвестными (6), которая является эквивалентной данной, то есть они или обе несовместны или же обе совместны и обладают одними и теми же решениями.

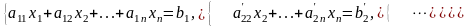(6)

Считаем, что среди этих уравнений нет таких, все коэффициенты левых частей которых равны нулю, эти уравнения будем исключать, если 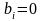, в противном случае система несовместна.

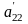
Далее первое уравнение не трогаем, и начинаем работать со вторым. Если коэффициент 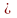0, то начинаем выполнять преобразования, аналогичные предыдущим, в противном случае поменяем строки местами или сделаем перенумерацию переменных. Преобразуем (6), вычитая из обеих частей третьего уравнения и из каждого следующего уравнения обе части второго уравнения, умноженные на числа: 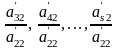соответственно. Этим мы исключим неизвестную 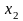из всех уравнений кроме первых двух. В результате получаем систему (7), эквивалентную системе (6), а, следовательно, и системе (5).

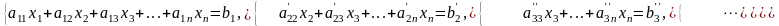(7)

Система (7) содержит 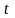уравнений, где т. к. некоторые уравнения могли быть отброшенными.

Данные преобразования выполняем до тех пор, пока не получим СЛУ 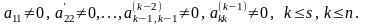(8):

(8)

В этом случае система совместна, определена при 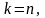не определена при

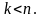
Если то (8) имеет вид:

линейный уравнение решение метод

(9)

Система (9) называется системой треугольного (ступенчатого) вида. Она обладает единственным решением, для нахождения которого необходимо из последнего уравнения найти 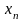, затем, двигаясь вверх по уравнениям системы определить значения остальных переменных, подставляя уже найденные переменные. Таким образом, система (9), а значит и эквивалентная ей (5) совместны и определены.

Если , то говорят, что система (8) имеет трапецеидальный вид и для нее существует бесчисленное множество решений. Чтобы найти общее решение данной системы неизвест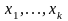ные , двигаясь по системе (8) снизу вверх, выражаем через переменные .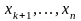

называются параметрами или свободными неизвестными. Придавая параметрам различные числовые значения, получим множество частных решений системы.

Данный метод применим к ОСЛУ. Однородная система всегда совместна, так как обладает нулевым решением (0,0 0). Если число неизвестных больше числа уравнений, то система неопределенна.

Рассмотренный метод также называют методом последовательного исключения неизвестных.