- •3)Ду 1-ого порядка и его решение. Изоклины. Поле направлений.
- •4. Задача Коши для ду 1-го порядка. Механическое истолкование ду 1-го порядка и его решений.
- •5. Теорема о существовании единственности решения ду 1-го порядка. Случай линейного ду 1-го порядка: выбор начальных данных и интервал существования решения.
- •6) Метод последовательных приближений решения ду 1-ого порядка.
- •9. Интегрирование ду 1-го порядка: уравнение, не содержащее искомой функции; уравнение, не содержащее независимой переменной.
- •2.Уравнения, не содержащие независимой переменной.
- •10. Интегрирование ду 1-го порядка: уравнение с разделёнными переменными; уравнение с разделяющими переменными.
- •14) Дифференциальные уравнения первого порядка, не разрешенные относительно производной Уравнения первого порядка n-ой степени относительно производной y'
- •3°. Уравнения Лагранжа и Клеро
- •18 Уравнения, допускающие понижение порядка
- •19. Линейные ду n-го порядка(однородные и неоднородные). Действительные и комплексные решения однородного линейного уравнения и их свойства
- •21)Линейные неоднородные дифференциальные уравнения второго
- •25. Метод неопределенных коэффициентов
- •26 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •27 Линейные однородные дифференциальные уравнение второго порядка с постоянными коэффициентами
- •28. Системы ду, основные понятия (нормальная система, теорема Коши…)
- •29. Достаточные и необходимые условия существования и единственности решения задачи Коши для нормальной системы. Понятие об общем и частном решениях.
28. Системы ду, основные понятия (нормальная система, теорема Коши…)
решение многих прикладных задач м требовать нахождения сразу нескольких неизвестных ф-ий. Для этого необходимо располагать таким же числом уравнений. Если каждое из этих уравнений явл-ся дифференциальным, т.е. содержит неизвестную ф-ию и её производную, независимую прм, то речь идет о системе ДУ, кот можно записать в виде:
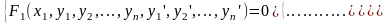
если разрешить каждое ур этой системы относ-но производной, то получим нормальную систему ДУ, при этом предполагается, что число уравнений=числу искомых ф-ий.
Решением этой системы наз-ся совокупность ф-ий у1, у2, …, уn, удовлетворяющих каждому из уравнений системы. Начальные условия для системы y1(x0)=y10, y2(x0)=y20, yn(x0)=yn0.(2)
На системы ДУ обобщается постановка задачи Коши для одного уравнения: найти решение системы (1), удовлетворяющее нач условиям (2).
Условие существования и единственности решения задачи Коши описывает теорема Коши: если в системе (1) все ф-ии fi(x,y1,y2,…,yn) непрерывны вместе со всеми своими частными производными по yi в некоторой области D (n+1)-мерного пространства, то в каждой точке M0(x0,y10,y20,…,yn0) этой области сущ-ет и при том единственное решение y1=φ1(x), y2= φ2(x),…, yn= φn(x) системы, удовлетвор нач условиям (2) в окрестности т х0.
Если менять т М0 в области D, т.е. нач условия, то получим бесчисленное множество решений, которые можно записать в виде решения зависящего от n произвольных постоянных: y1=φ1(x,c1,c2,…,cn), y2= φ2(x,c1,c2,…,cn),…,yn= φn(x,c1,c2,…,cn). Это решение явл общим, если по заданным н.у. можно однозначно определить пост с1,с2,…, сn из системы уравнений:

частным решением наз-ся решение, которое получается из общего при конкретных значениях постоянных с1, с2, …, сn.
К системе ДУ 1ого порядка во многих случаях сводится уравнения и системы уравнений высших порядков. Например: y”’=f(x,y,y’,y”). обозначим y’и y” ч/з u и v соответственно. Тогда уравнение можно заменить системой

29. Достаточные и необходимые условия существования и единственности решения задачи Коши для нормальной системы. Понятие об общем и частном решениях.
Нормальную систему ДУ можно получить в результате разрешения относительно производной системы ДУ, состоящей из n уравнений и имеющей вид
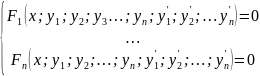
Нормальная система имеет вид:
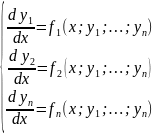 (1)
(1)
Предполагается, что число уравнений равно числу искомых функций.
Решение системы (1) – совокупность функций ,… , удовлетворяющих каждому из уравнений этой системы.
Начальные условия для системы (1) имеют вид:
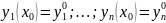 (2)
(2)
Условия существования и единственности решения задачи Коши описывает т. Коши:
Если
в системе (1) все функции
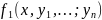 непрерывны вместе со своими частными
производными по
непрерывны вместе со своими частными
производными по
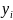 некоторой области D
((α+1)
– мерного пространства), то в каждой
точке
некоторой области D
((α+1)
– мерного пространства), то в каждой
точке
 этой области существует единственное
решение
этой области существует единственное
решение
 системы, удовлетворяющее начальным
условиям (2) окрестности точки
системы, удовлетворяющее начальным
условиям (2) окрестности точки
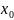 .
.
Если
менять точку
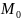 в области D
(т.е. начальные условия), получим
бесчисленное множество решений, которое
можно записать в виде решения, зависящего
от n
производных постоянных
в области D
(т.е. начальные условия), получим
бесчисленное множество решений, которое
можно записать в виде решения, зависящего
от n
производных постоянных
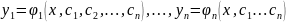
Это
решение является общим, если по заданным
начальным условиям можно однозначно
определить постоянные
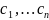 из системы уравнений
из системы уравнений
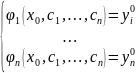
Частным
решением называется решение, которое
получается из общего при конкретных
значениях постоянных
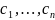 .
.
Следует заметить, что к системам ДУ первого порядка во многих случаях сводится уравнения и системы уравнений высших порядков.
Пример:
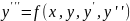
Обозначим
и запишем системы
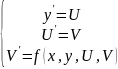
Аналогичное истолкование допускает любое другое ДУ или система уравнений.
30) СВЯЗЬ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ И СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Задача Коши для любого дифференциального уравнения n–го порядка, записанного в нормальной форме,
y(n)= F(x, y, y ', y '', … , y(n−1) ) = 0, y(x0) = y0, y '(x0) = y1, y ''(x0) = y2, … , y(n − 1) (x0) = yn− 1 ,
может быть сведена к задаче Коши для системы дифференциальных уравнений n– го порядка.
Обозначим
z1(x) = y(x), z2(x) = y'(x), z3 (x) = y ''(x), … , zn( x) = y (n − 1)(x ).
Тогда
F(x, y, y ', y '', … , y(n−1)) ≡ F(x, z1, z2, z3, … , zn)
и задача Коши для уравнения записывается в виде задачи Коши для системы
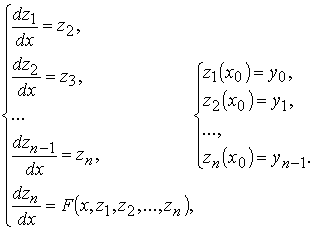
Эта задача в векторной форме записывается в виде:
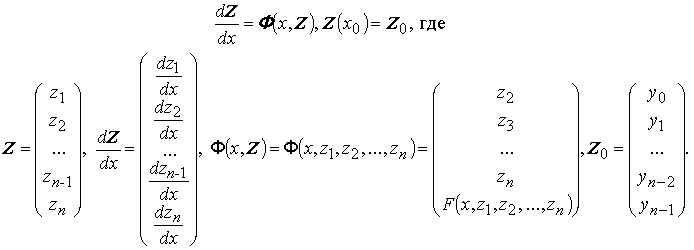
31)Однородные системы
Однородной
системой линейных уравнений называется
система вида:
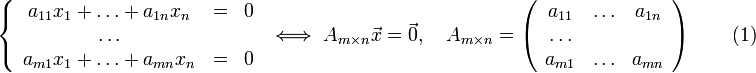
|
Теорема
(о линейном решении однородных
систем).
Пусть
|
|
||
|
Пусть
дана однородная система (1), тогда
набор векторов
|
|
Неоднородные системы
Неоднородной
системой
линейных уравнений
называется система вида:
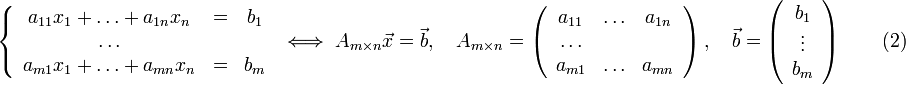
![]() —
её
расширенная матрица.
—
её
расширенная матрица.
Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.
Средством изучения линейной зависимости системы функций является так называемый определитель Вронского (Вронскиан)
Для 2-х дифференциальных уравнений y1=y1(x) и y2=y2(x) определитель Вронского имеет вид:
W(x)=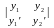
Теорема 2.2.: если дифференциальные функции y1(x) и y2(x) линейно зависимы на (a;b), то составленный из них определитель Вронского на этом интервале тождественно равен 0
Т.к. y1(x) и y2(x) линейно зависимы, то в равенстве: α1y1(x)+α2y2(x)=0 α1 или α2 ≠0
Пусть α1≠0, тогда y1=-(α2/α1)y2
Поэтому
для всех x
принадлежащих (a;b):
W(x)=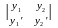 =
= =0
=0
что и требовалось доказать
Теорема 2.3. Если решения y1(x) и y2(x) уравнения (2.1) линейно независимы на интервале (a;b), то составленный из них определитель Вронского отличен от 0 на этом интервале
замечание: из теорем 2.2. и 2.3. следует, что W(x)≠0 ни в одной точке (a;b) т.т.т., когда частные решения линейно независимы.
совокупность любых двух линейно независимых на интервале (a;b) частных решений y1(x) и y2(x) уравнения (2.1) определяют фундаментальную систему решений этого уравнения: любое произвольное решение м.б. получено как комбинация y=α1y1(x)+α2y2(x). Теперь можно сказать, при каких условиях функция y=C1y1(x)+C2y2(x) будет общим решением.
32)Рассмотрим этот метод в применении к системе трех линейных дифференциальных уравнений:
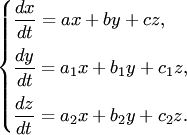 (3)
(3)
Решение системы (3) ищем в виде
![]() (4)
(4)
Подставляя
(4) в (3) и сокращая на
![]() ,
получаем систему уравнений для определения
,
получаем систему уравнений для определения
![]() и
и
![]()
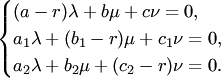 (5)
(5)
Система
(5) имеет ненулевое решение, когда ее
определитель
![]() равен
нулю,
равен
нулю,
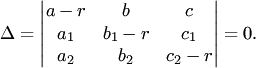 (6)
(6)
Уравнение (6) называется характеристическим.
А.
Пусть корни
![]() и
и
![]() характеристического
уравнения — вещественные
и различные.
Подставив в (5) вместо
характеристического
уравнения — вещественные
и различные.
Подставив в (5) вместо
![]() число
число
![]() и
решив систему (5), получим числа
и
решив систему (5), получим числа
![]() и
и
![]() .
Затем положим в (5)
.
Затем положим в (5)
![]() и
получим числа
и
получим числа
![]() и,
наконец, при
и,
наконец, при
![]() получим
получим
![]() и
и
![]() .
Соответственно трем наборам чисел
и
.
Соответственно трем наборам чисел
и
![]() получим
три частных решения
получим
три частных решения
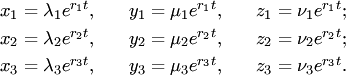
Общее решение системы (3) имеет вид