Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов и любых действительных чисел справедливы равенства:

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.

Линейные комбинации векторов

Применяя линейные операции, можно составлять суммы векторов, умноженных на числа.

Вектор называется линейной комбинацией векторов , если он может быть представлен в виде

,

где — некоторые числа. В этом случае говорят, что вектор разложен по векторам , а числа называют коэффициентами разложения.

Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Отметим следующие свойства линейных комбинаций векторов:

1. Если векторы — коллинеарны, то любая их линейная комбинация им коллинеарна.

2. Если векторы — компланарны, то любая их линейная комбинация им компланарна.

Докажем, например, первое свойство. При умножении вектора на число получаем (по определению) вектор, колпинеарный данному. При сложении двух векторов, параллельных некоторой прямой, получаем (по определению) вектор, параллельный той же самой прямой. Поэтому линейная комбинация двух коллинеарных векторов и коллинеарна им. По индукции свойство распространяется на любое конечное число коллинеарных векторов.

8.

Проекция вектора но ось и её свойства

О: Проекцией т. на ось именуется основание перпендикуляра , который опущен из т. на : . Составляющей вектора по оси является число . Используется знак (+) , если , и знак (-) — когда .В том случае если является единичным вектором (то есть ) в направлении , то .

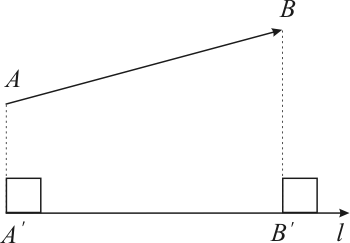
Рис. 2.7

Свойства проекций

1⁰. , где .

Если , тогда из получаем (рис. 2.8).

Если , то (рис. 2.9).

2⁰. Проекция суммы векторов на ось равна сумме проекций векторов на .

Доказательство будет геометрическим (рис 2.10).

 

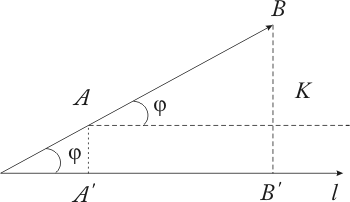
Рис. 2.8

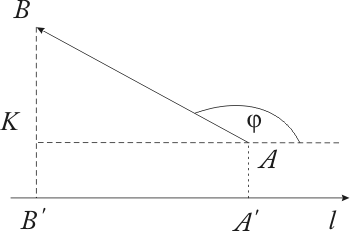
Рис. 2.9

 

Рис. 2.10

3⁰. . доказательство осуществляется исходя из свойства 1⁰.

9.

Координаты вектора

На плоскости координаты вектора v относительно данного базиса (a, b) – это такая пара чисел (x; y), что v = xa + yb. Любой вектор имеет однозначно определенные координаты относительно любого базиса.

При сложении векторов складываются их соответственные координаты; при умножении вектора на число каждая координата умножается на это число. Скалярное произведение векторов с координатами (x; y) и (x'; y') равно сумме произведений соответственных координат: xx' + yy'.

Чтобы вычислить координаты вектора , зная координаты (x₁; y₁) его начала A и координаты (x₂; y₂) его конца B, нужно из координат конца вычесть координаты начала: (x₂ – x₁; y₂ – y₁).

Все сказанное справедливо и для случая пространства с той разницей, что базис в пространстве состоит из трех векторов, а наборы координат векторов и точек – из трех чисел.