10. Транспонирование матриц.

Определение 1. Пусть A = (aij) (n x m). Транспонирование матрицы — это такое ее преобразование, при котором строка с номером i записывается в столбец с тем же номером.

Обозначение: А^t , А^tr , А'.

Пример:

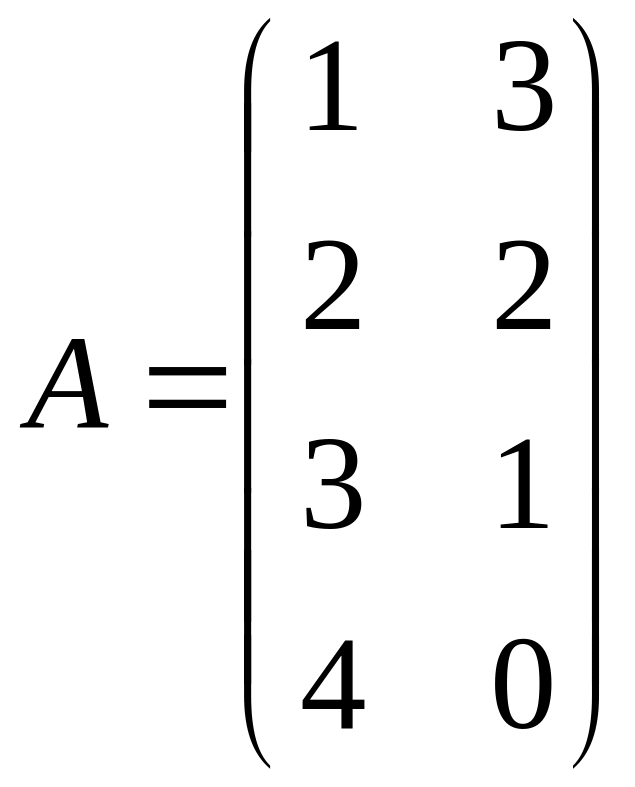, то .

Теорема 5. Имеют место следующие равенства:

1. (А^t)^t = A.

2. (αA + βB)^t = αA^t + βB^t.

3. (AB)^t = В^tА^t .

Причем, А и В — матрицы подходящих размеров, α и β — любые числа.

< 1. А = (а_ij)_{m x n}

(A)^t = (а_ji)_{n x m}  (А^t)^t = A.

3. Пусть имеем А = (а_ij)_{m x n} и B = (b_ij)_{n x s} . Тогда A(^t) = ( ij) (m x n) , B (^t)=( ij) (s x m), AB = (cij) (m x s), (BА)(^t) = (dij)(s x m)

Матрица В(^t)A(^t) и AB)(^t)одинаковых размеров, и чтобы доказать, что В(^t)A(^t) = (AB)(^t), надо показать, что на одинаковых местах стоят одинаковые элементы.

Мы получили, что на позиции ij у матрицы В(^t)A(^t) и матрицы AB)(^t) стоит один и тот же элемент. >

Определение 2. Матрица А называется симметрической, если A(^t) = А, и кососимметрической, если A(^t) = -А.

Пример. Симметрическая матрица:

кососимметрическая матрица:

11. Перестановки.

Пусть X — непустое множество элементов произвольной природы, так как природа элементов для нас несущественна, то в случае конечного множества считаем X ={1,2,3,…,n}

Определение 1. Любое упорядоченное расположение элементов множества X называется перестановкой множества X.

Пример:

Если X ={1,2,3,4,5} , то (2,5,3,4,1) - перестановка множества X.

Перестановку элементов множества X обозначают(a1,a2,…,an), причем среди ai (i = 1,2,…, n) нет равных.

Определение 2. Две перестановки множества X называются равными, если у них на одинаковых местах стоят одинаковые элементы.

Теорема 1. Число различных перестановок множества из n элементов равно n!

< Докажем эту теорему индукцией по числу n. При n=1 имеется одна перестановка, т.е. 1!.

Пусть n>1 и число различных перестановок, которые можно составить из заданных (n-1) элементов, равно (n-1)!. Всякая перестановка данных элементов с фиксированным первым числом а имеет вид:

a1,a2,…,an.

где a2,…,an произвольная перестановка оставшихся (n-1) элементов. По индуктивному предположению число таких перестановок равно (n-1)!. В качестве а, можно взять любой из данных n элементов, поэтому число различных перестановок заданных n элементов равно сумме n слагаемых, каждое из которых есть(n-1)!, т.е. n! >

Определение 3. Будем говорить, что в перестановке чисел (a1,a2,…,an) два числа ai,aj образуют инверсию если ai>aj, но i < j. В противном случае ai,aj образуют порядок.

Пример:

В перестановке (1 3 4 2) инверсии: 4,2 ; 3,2 , а остальные пары образуют порядок.

Определение 4. Количество пар чисел, образующих инверсию в перестановке, называют числом инверсий данной перестановки. Отображение XX будем называть преобразованием множества X.

Пусть множество X состоит не менее чем из двух элементов a,bX.

Определение 5. Преобразование множества Х называют транспозицией элементов a и b, если , ,  xa,b.Такое преобразование обозначают (a,b).

Определение 6. Перестановку называют четной, если число инверсий в ней четно, и нечетной в противном случае.

Теорема 2. Однократное применение транспозиции к перестановке изменяет ее характер четности на противоположный.

< Пусть имеется перестановка (a1,…,a,…,b,…an) (1) . Применим к ней транспозицию(a,b), получим(a1,…,b,…,a,…an) (2). Рассмотрим несколько случаев:

1. Пусть a и b стоят рядом. Если a и b в (1) образуют инверсию, то (2) образуют порядок. Поэтому характер четности изменяется на противоположный, ибо число инверсий изменяется на единицу.

2. Пусть a и b не стоят рядом (a1,…,a,…,b,…an). От (1) к (2) можно перейти следующим способом: a менять с рядом стоящим элементом дойти до b и b перегнать на место a. Всего нам придется применить S+1+S=2S+1 транспозиций соседних чисел, где S число элементов между a и b, поэтому характер четности перестановок (1) и (2) различны.>

Следствие. При n2 число четных перестановок равно числу нечетных перестановок и равно n!/2.

< Пусть число четных перестановок равно S, нечетных — T. Если к каждой четной перестановке мы применим транспозицию двух элементов, мы превратим их в нечетные ST, аналогично наоборот T S  T=S

n!=S+T =2S

S=T=n!/2. >

Теорема 3. Пусть даны две различные перестановки одних и тех же чисел, тогда существует последовательность транспозиций переводящих первую перестановку во вторую.

< Пусть (a1,a2,…,an) (3) (b1,b2,…,bn) (4)

есть произвольные перестановки из n чисел. Если a12, то применив к перестановке (3) транспозицию (a1,b2) получим перестановку n чисел вида

(b1,2,3,…,n) (5)

Если 2b2, то к перестановке (5) применим транспозицию (2,b2).В результате получим перестановку (b1,b2,3,…n). Продолжаем этот процесс получаем требуемое.>