Вопрос 4.

Выводимость исчисления высказываний.

Математическая логика основана на понятии простого высказывания. Простое высказывание – это утверждение, про которое можно сказать, истинно оно или ложно при данных условиях. Из простых высказываний с помощью логических операций строятся составные высказывания, которые далее будут называться просто высказываниями. Сохраняющее эти операции сопоставление каждому высказыванию одного из значений «истина» или «ложь», обозначаемых соответственно 1 или 0, называется интерпретацией исчисления высказываний.

Алфавитом называется произвольное множество. Его элементы называются символами. Произвольная конечная последовательность символов называется словом. Слово может быть пустым.

Исчисление высказываний определяется следующим образом:

Его алфавит состоит из символов , называемых логическими, и из символов, принадлежащих произвольному множеству Р, называемых нелогическими символами или буквами.

Метод миров.

Он заключается в том, что позволяет целенаправленно искать вывод заданной формулы, раскладывая задачу поиска вывода на аналогичные, но более простые подзадачи. Формула выводима тогда и только тогда, когда не существует логики высказываний, в которой эта формула ложна. Определяется это путем построения логического дерева миров с помощью 8 правил.

(Если вы читаете то, что я пишу, то правила скатайте с тетради))))

Когда какой-либо мир противоречит предыдущему, то этот мир погибает. Если по окончанию всего разложения вес миры погибли, то данное выражение является выводимым.

Метод резолюций Робинсона.

Метод, который позволяет устанавливать невыполнимость любой КНФ, если она действительно невыполнима. Мы увидим, что задача установления общезначимости любой формулы сводится к задаче установления невыполнимости некоторой КНФ, построенной по исходной формуле.

Для того, чтобы применить к данному выражению метод резолюций, необходимо его преобразовать:

1. Перед знаком выводимость все выражение привести к виду КНФ

2. После знака выводимости все выражение привести к виду ДНФ

3. Перенести ДНФ с инверсией в левую часть, образую новый конъюнкт.

Метод резолюций базируется на обобщении указанного наблюдения. Он основан на следующем правиле образования нового дизъюнкта из двух дизъюнктов: из одного дизъюнкта вычёркиваем переменную, из другого — её отрицание, и из всех остальных литер двух исходных дизъюнктов составляем новый дизъюнкт. Процедуру сокращения дизъюнктов мы продолжаем до тех пор, пока не получим пустое множество дизъюнктов. Это и будет говорить о том, что данное логическое выражение является выводимым.

Вопрос 5.

Выводимость исчисления высказываний.

Математическая логика основана на понятии простого высказывания. Простое высказывание – это утверждение, про которое можно сказать, истинно оно или ложно при данных условиях. Из простых высказываний с помощью логических операций строятся составные высказывания, которые далее будут называться просто высказываниями. Сохраняющее эти операции сопоставление каждому высказыванию одного из значений «истина» или «ложь», обозначаемых соответственно 1 или 0, называется интерпретацией исчисления высказываний.

Алфавитом называется произвольное множество. Его элементы называются символами. Произвольная конечная последовательность символов называется словом. Слово может быть пустым.

Исчисление высказываний определяется следующим образом:

Его алфавит состоит из символов , называемых логическими, и из символов, принадлежащих произвольному множеству Р, называемых нелогическими символами или буквами.

Метод Вонга.

В этом методе используется сконструированная конъюнктивно - нормальная форма:

X,L  X;R

Здесь X пробегает некоторые буквы, входящие в клаузу, а L и R- определенные комбинации дизъюнктов и конъюнктов.

Для того, чтобы придти к такому виду выражения, необходимо выполнить ряд условий:

1. Замена импликации в строке на ДНФ:

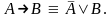
2. Избавление от знака отрицания « » переносом из одной части строки в другую.

3. Расщепление на строки (левой и правой части строки Вонга).

4. Замена логических связок на «,» (правило перечисления).

5. Критерий доказательства вывода. В результате освобождения строки Вонга от логических связок имеем 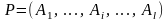⊦ 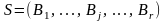, т.е. строка Вонга имеет вид:

⊦ .

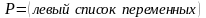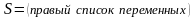Если в левом списке и правом списке найдутся одинаковые переменные, то из P выводимо S (P ⊦.S).

Конструктивная процедура доказательства сводится к последовательному разбиению дизъюнктов и конъюнктов таким образом, чтобы слева и справа от импликации появилась одна и та же буква Х. Если в результате такого разбиения все конечные клаузы приобретают вид клаузы Вонга, то и исходная клауза была составлена верно. При большом числе букв в исходной клаузе прибегают к специальной нумерации производных клауз, чтобы не запутаться.

Метод Маслова.

Представим исходную формулу Ф в виде чисел с индексами следующим образом. Каждому дизъюнкту исходной формулы поставим в соответствие порядковый номер этого дизъюнкта в формуле (число без индекса), а каждой букве— число с индексом, где число обозначает номер дизъюнкта, а индекс - порядковый номер данной буквы в этом дизъюнкте. Если дизъюнкт состоит из одной буквы, то буква этого дизъюнкта получает в качестве кода число с индексом ноль. Тогда Ф например будет выглядеть так: 1₀  2₁2₂  3₁3₂3₃  4₁4₂  5₁5₂  6₁6₂6₃  7₁7₂7₃

Существенной чертой данной кодировки является то, что теперь каждая буква получает свой номер — число с индексом, — несмотря на то, что они могут представлять одну и ту же переменную. Такая кодировка совместно с обычным представлением формул исчисления высказываний позволяет более полно представить структуру формул и выводов.

Метод Маслова так же называется методом благоприятных наборов.

НАБОРОМ называется последовательность чисел с индексами, где графически равные члены сокращаются до одного и порядок записи чисел с индексами несущественен. Набор записывается в строчку без скобок.

НАБОРОМ С ЗАВИСИМОСТЬЮ называется набор, справа от которого в круглых скобках приписана некоторая последовательность чисел без индексов (в зависимости порядок записи числе также несущественен и графически равные члены сокращаются до одного).

ВЫВОДОМ называется линейная последовательность благоприятных наборов с зависимостями, последним членом которой является пустой (нольчленный) благоприятный набор (он обозначен знаком ).

(Сам порядок выполнения я не писала, потому что бред получиться, кому нужно на словах объясню)