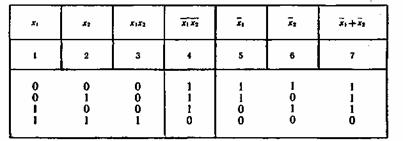
Вопрос 1.

В булевой алгебре используются четыре основных закона: переместительный, сочетательный, распределительный, инверсии. Эти законы позволяют проводить эквивалентные преобразования ПФ(праивльная форма), записанных с помощью операций НЕ, И, ИЛИ, т. е. приводить выражения ПФ к удобному (более простому) виду.

 Переместительный закон аналогичен переместительному закону обычной алгебры и записывается в виде:

а) для дизъюнкции

(3.1)

б) для конъюнкции

(3.2)

Таким образом, от перемены мест слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.

 Сочетательный закон также аналогичен сочетательному закону обычной алгебры и записывается в виде:

а) для дизъюнкции

(3.3)

б) для конъюнкции

(3.4)

Следовательно, можно группировать переменные, объединенные знаком дизъюнкции или конъюнкции, это не меняет значений ПФ.

 Распределительный закон записывается в виде:

а) для дизъюнкции

(3.5)

т. е. дизъюнкция переменной и конъюнкции равносильна конъюнкции дизъюнкций этой переменной с сомножителями;

б) для конъюнкции

(3.6)

т. е. конъюнкция переменной и дизъюнкции эквивалентна дизъюнкции конъюнкций этой переменной со слагаемыми.

Справедливость выражения (3.5) доказывается путем г составления таблиц истинности для левой и правой частей. Значения этих таблиц совпадают для одинаковых наборов переменных, это и доказывает справедливость (3.5).

Закон инверсии:

а) для дизъюнкции

(3.7)

т. е. отрицание дизъюнкции логических переменных эквивалентно конъюнкции отрицаний этих переменных;

б) для конъюнкции

(3.8)

т. е. отрицание конъюнкции переменных эквивалентно дизъюнкции отрицаний этих переменных.

Из законов алгебры логики выводится ряд важных правил, которые полезны при выполнении эквивалентных преобразований ПФ.

1. Выражения, имеющие всегда значение 1:

2.Выражения, имеющие всегда значение 0:

3. Двойное отрицание:

4.Повторение:

5.Склеивание: .

Это правило доказывается путем вынесения в левой части х₁ за скобку и применения правила 1 для выражения, имеющего значение 1:

6.Поглощение:

Для доказательства справедливости этого правила вынесем в левой части за скобку х₁ и применим правило 1 для выражения, имеющего значение 1:

Дизъюнктивная нормальная форма(ДНФ) и СДНФ. Конъюнктивная нормальная форма(КНФ) и СКНФ.

    Конъюнкция и дизъюнкция

  Определение 1: Конъюнкцией(или логическое умножение) двух булевых переменных называется следующая функция .

     Определение 2: Дизъюнкцией(логическое сложение) двух булевых переменных называется следующая функция .

     Определение 3: Дизъюнкция конечного множества элементарных конъюнкций называется дизъюнктивной нормальной формой(ДНФ). Число элементарных конъюнкций, образующих дизъюнктивную нормальную форму(ДНФ) называется длиной ДНФ. ДНФ содержащая только полные элементарные конъюнкции называется совершенной ДНФ(или СДНФ). Любую логическую формулу А можно представить в виде ДНФ, а затем ДНФ в виде СДНФ.

     Алгоритм построения СДНФ:

     Легко построить СДНФ, представляющую произвольную булеву функцию, заданную в табличной форме. Для этого достаточно выделить наборы , на которых функция принимает значение 1, и для каждого из них ввести в СДНФ полную элементарную конъюнкцию, где любая переменная присутствует с отрицанием, если , и без отрицания, если . Очевидно, для любой булевой функции , кроме константы 0, существует единственная СДНФ (с точностью до порядка литералов и конъюнкций). Поэтому данная форма представления булевой функции является канонической.

Конъюнктивная нормальная форма(КНФ)

         Определение 4: Конъюнкция конечного множества элементарных дизъюнкций называется конъюнктивной нормальной формой(или сокращенно КНФ). Число элементарных дизъюнкций образующих КНФ называется длинной. КНФ состоящая только из полных элементарных дизъюнкций называется СКНФ. Произвольную формулу B vможно представить в виде КНФ, а затем КНФ в виде СКНФ.

     Алгоритм построения СКНФ:

     СКНФ, представляющую произвольную булеву функцию, так же, как ее СДНФ, легко построить по табличному заданию этой функции. Согласно формуле достаточно выделить наборы , на которых функция принимает значение 0, и для каждого из них ввести в СДНФ полную элементарную дизъюнкцию, где любая переменная присутствует с отрицанием, если , и без отрицания, если .      Очевидно, для любой булевой функции , кроме константы 1, существует единственная СКНФ (с точностью до порядка литералов и дизъюнкций). Так же, как СДНФ, эта форма представления булевой функции является канонической.