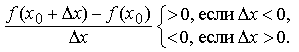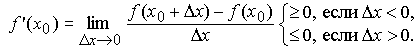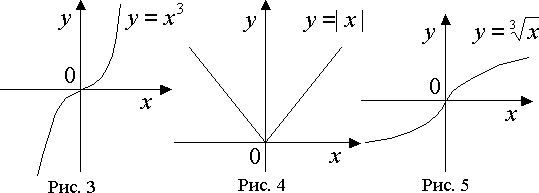|
|
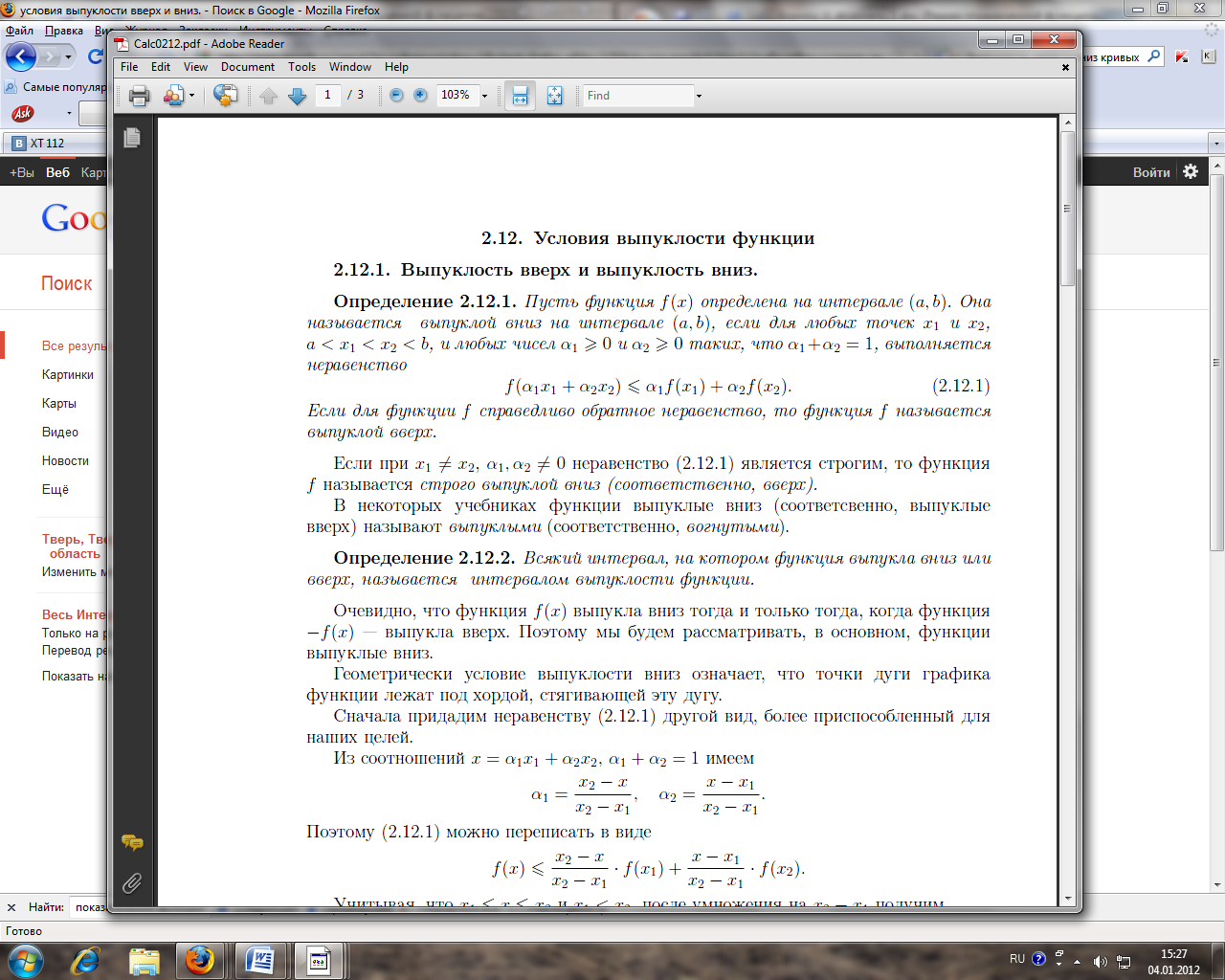
График 1.3.7.1.
Эта функция непрерывна в точке A и
разрывна в точке B
|
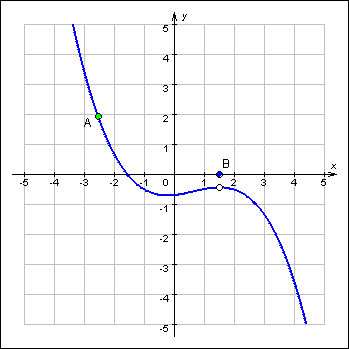
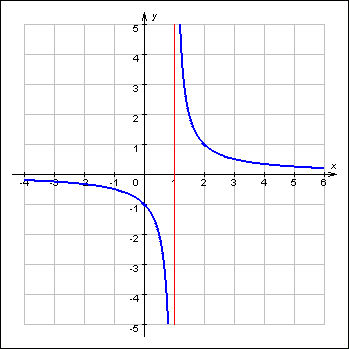
График 1.3.7.2.
На
рисунке показана функция
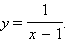 Она
разрывна в точке x0 = 1,
так как не существует в этой точке.
Она
разрывна в точке x0 = 1,
так как не существует в этой точке.
|
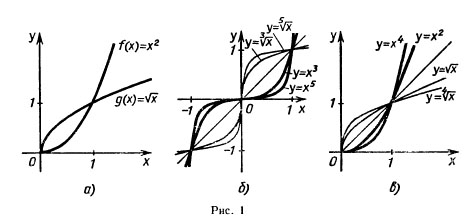
Примером
разрывной функции может служить функция
зависимости плотности воды в окрестности
0 ºC. Примером непрерывной функции
является зависимость площади квадрата
от длины его стороны. Подчеркнем еще
раз, что непрерывность функции
рассматривается только на области ее
определения.
Если
функция непрерывна в каждой точке
некоторого промежутка, то она называется
непрерывной на этом промежутке.
Большинство функций, изучаемых в
элементарной математике, непрерывны
на всей области определения. Таковыми
являются линейная функция y = kx + b,
квадратичная y = ax2 + bx + c,
показательная
и тригонометрические
функции.
Если
функции f (x)
и g (x)
непрерывны в точке x0,
то их сумма и произведение также
непрерывны в этой точке, а функция
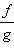 непрерывна
в ней при условии, что g (x0) ≠ 0.
непрерывна
в ней при условии, что g (x0) ≠ 0.
Отсюда
следует, что рациональные функции
непрерывны во всех тех точках, в которых
их знаменатель не обращается в нуль.
Из
непрерывности функции y = f (x)
в точке x0
и функции z = g (y)
в точке y = f (x0)
следует непрерывность сложной функции
g (f (x))
в точке x0.
Функцию f (x)
называют непрерывной
на отрезке
[a; b],
если она непрерывна в каждой точке
интервала (a; b)
и, кроме того, непрерывна справа в точке
a
и слева в точке b.
Т еорема
Вейерштрасса.
Если функция f (x)
непрерывна на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.
еорема
Вейерштрасса.
Если функция f (x)
непрерывна на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.
1
|
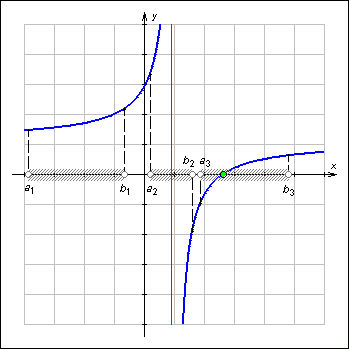
Рисунок 1.3.7.1.
Теорема
Коши о нулях непрерывной функции.
Только на одном из отрезков – [a3; b3] –
имеется нуль функции, так как на
этом отрезке функция непрерывна и
принимает значения разных знаков на
концах
|
Т
еорема
Коши. Если
функция f (x)
непрерывна на отрезке [a; b]
и принимает на его концах значения
разных знаков, то на отрезке [a; b]
имеется хотя бы один нуль функции f.
При этом, если функция строго монотонна
на этом отрезке, то она принимает
значение 0 лишь один раз.
Т
еорема
о промежуточных значениях.
Если функция f (x)
непрерывна на отрезке [a; b]
и f (a) ≠ f (b),
то для каждого значения y,
заключенного между f (a) и
f (b),
найдется точка
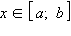 (и
возможно, не одна) такая, что f (x) = y.
(и
возможно, не одна) такая, что f (x) = y.
Теорема
Коши́ о среднем значении.
-
Пусть даны две
функции
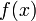 и
и
 такие,
что:
такие,
что:
и
определены
и непрерывны на отрезке
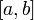 ;
;
производные
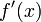 и
и
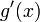 конечны
на интервале
конечны
на интервале
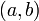 ;
;
производные
и
не
обращаются в ноль одновременно на
интервале
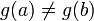 ;
;
тогда
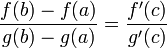 ,
где
,
где

(Если
убрать условие 4, то необходимо
усилить условие 3: g'(x) не должна
обращаться в ноль нигде в интервале
(a,b).)
|
Геометрически
это можно переформулировать так: если
f
и g
задают законы движения на плоскости
(то есть определяют абсциссу и ординату
через параметр t),
то на любом отрезке такой кривой,
заданном параметрами a
и b,
найдётся касательный вектор,
коллинеарный
вектору перемещения от (f(a);g(a))
до (f(b);g(b)).
[Править] Доказательство
Для
доказательства введём функцию
Для
неё выполнены условия теоремы
Ролля:
на концах отрезка её значения равны
f(a).
Воспользовавшись упомянутой теоремой,
получим, что существует точка c,
в которой производная функции F
равна нулю, а
 равна
как раз необходимому числу.
равна
как раз необходимому числу.
Теоре́ма
Вейерштра́сса
в математическом
анализе
и общей
топологии
гласит, что функция, непрерывная на
компакте,
ограничена на нём и достигает своей
верхней и нижней грани.
Формулировка
Пусть
дана непрерывная
числовая
функция,
определённая на отрезке,
то есть
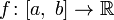 и
и
 .
Пусть
.
Пусть
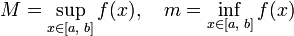
—
точные верхняя
и нижняя
грани множества
значений
функции f
соответственно. Тогда эти значения
конечны (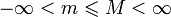 )
и достигаются (существуют
)
и достигаются (существуют
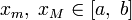 такие,
что
такие,
что
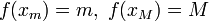 ).
).
п·о·р
Доказательство [показать]
[Править] Доказательство для r
Пусть
f(x)
— функция, отвечающая условиям теоремы
(на компакте A),
M
= sup Af.
Возьмём последовательность чисел am
таких, что lim am
= M
и am
< M.
Для каждого m
найдётся точка xm,
такая что am
< f(xm).
Имеем дело с компактом, поэтому, согласно
теореме
Больцано — Вейерштрасса
из последовательности xm
можно выделить сходящуюся последовательность
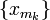 ,
предел которой лежит в A.
,
предел которой лежит в A.
Для
любого xm
справедливо
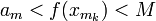 ,
поэтому, применяя предельный
переход,
получаем
,
поэтому, применяя предельный
переход,
получаем
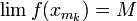 и
в силу непрерывности функции существует
точка x0
такая, что
и
в силу непрерывности функции существует
точка x0
такая, что
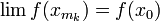 и,
следовательно M
= f(x0).
и,
следовательно M
= f(x0).
Таким
образом функция f(x)
ограничена и достигает своей верхней
грани при x
= x0.
Аналогично и для нижней грани.
[Править] Замечания
По
определению точки xm
и xM
являются точками
глобального минимума
и максимума
соответственно. Таким образом непрерывная
на отрезке функция достигает на нём
своего минимума
и максимума.
В
предположениях теоремы отрезок нельзя
заменить на открытый
интервал.
Например, функция тангенс
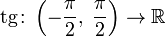
непрерывна
в каждой точке области
определения,
но не ограничена.
[править]
Обобщения
[править]
Теорема
Вейерштрасса для полунепрерывных
функций
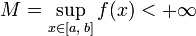 и
и
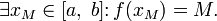
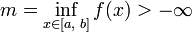 и
и
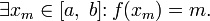
[править]
Теорема
Вейерштрасса для непрерывных функций
на компакте
Пусть
дано топологическое
пространство
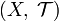 и
компактное
подмножество
и
компактное
подмножество
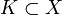 .
Пусть дана непрерывная функция
.
Пусть дана непрерывная функция
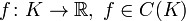 .
Тогда
.
Тогда
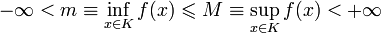
и
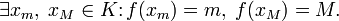
70
Первый
замечательный предел
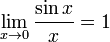
Доказательство
Рассмотрим
односторонние
пределы
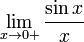 и
и
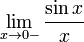 и
докажем, что они равны 1.
и
докажем, что они равны 1.
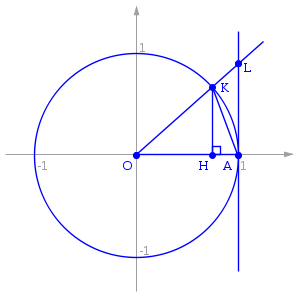
Пусть
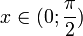 .
Отложим этот угол на единичной окружности
(R
= 1).
.
Отложим этот угол на единичной окружности
(R
= 1).
Точка
K —
точка пересечения луча с окружностью,
а точка L —
с касательной к единичной окружности
в точке (1;0).
Точка H —
проекция точки K
на ось OX.
Очевидно,
что:
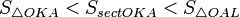 (1)
(1)
(где
SsectOKA —
площадь сектора OKA)
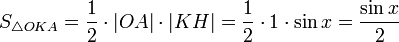
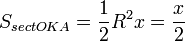
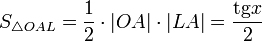
(из
 :
| LA
| = tgx)
:
| LA
| = tgx)
Подставляя
в (1), получим:
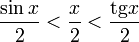
Так
как при
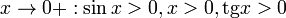 :
:
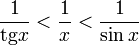
Умножаем
на sinx:
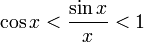
Перейдём
к пределу:
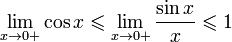
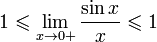
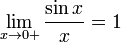
Найдём
левый односторонний предел:
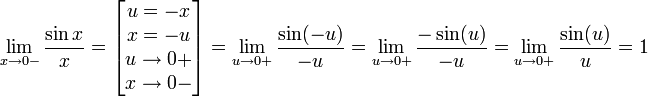
Правый
и левый односторонний пределы существуют
и равны 1, а значит и сам предел равен
1.
Следствия
71
72
Второй замечательный предел
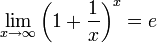 или
или
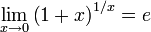
Доказательство
второго замечательного предела:
Доказательство
для натуральных значений x [показать]
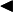 Докажем
вначале теорему для случая последовательности
Докажем
вначале теорему для случая последовательности
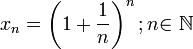
По
формуле бинома
Ньютона:
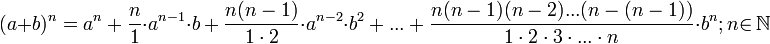
Полагая
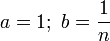 ,
получим:
,
получим:
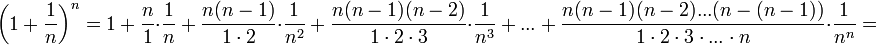
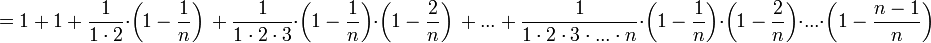 (1)
(1)
Из
данного равенства (1) следует, что с
увеличением n число положительных
слагаемых в правой части увеличивается.
Кроме того, при увеличении n число
 убывает,
поэтому величины
убывает,
поэтому величины
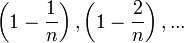 возрастают.
Поэтому последовательность
возрастают.
Поэтому последовательность
 —
возрастающая,
при этом
—
возрастающая,
при этом
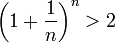 (2).
(2).
Покажем, что она
ограничена. Заменим каждую скобку в
правой части равенства на единицу,
правая часть увеличится, получим
неравенство

Усилим полученное
неравенство, заменим 3,4,5, …, стоящие в
знаменателях дробей, числом 2:
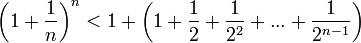 .
.
Сумму в скобке
найдём по формуле суммы членов
геометрической прогрессии:
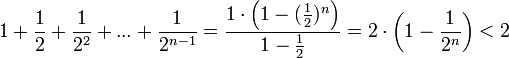 .
.
Поэтому
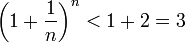 (3).
(3).
Итак,
последовательность ограничена сверху,
при этом
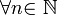 выполняются
неравенства (2) и (3):
выполняются
неравенства (2) и (3):
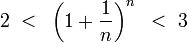 .
.
Следовательно,
на основании теоремы Вейерштрасса
(критерий сходимости последовательности)
последовательность
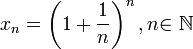 монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е.
монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е.
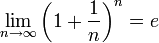

Зная, что второй
замечательный предел верен для
натуральных значений x, докажем второй
замечательный предел для вещественных
x, то есть докажем, что
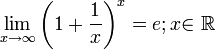 .
Рассмотрим два случая:
.
Рассмотрим два случая:
1.
Пусть
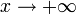 .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами:
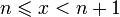 ,
где
,
где
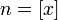 —
это целая часть x.
—
это целая часть x.
Отсюда следует:
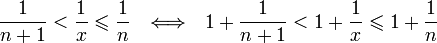 ,
поэтому
,
поэтому
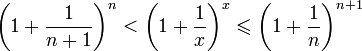 .
.
Если
,
то
 .
Поэтому, согласно пределу
,
имеем:
.
Поэтому, согласно пределу
,
имеем:
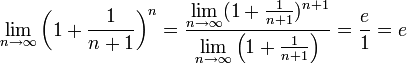
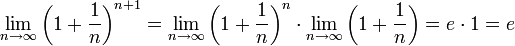 .
.
По признаку (о
пределе промежуточной функции)
существования пределов
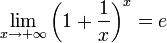 .
.
2.
Пусть
 .
Сделаем подстановку −
x
= t,
тогда
.
Сделаем подстановку −
x
= t,
тогда
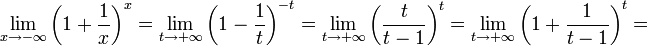
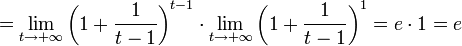 .
.
Из
двух этих случаев вытекает, что
для
вещественного x.
Следствия
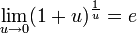
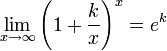
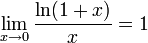
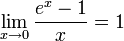
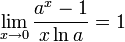 для
для
 ,
,
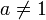
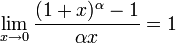
Натуральные логарифмы
Основная статья:
Натуральный
логарифм
Связь
с десятичным логарифмом:
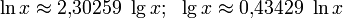 .
.
Как
указано выше, для производной
натурального логарифма справедлива
простая формула:
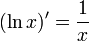
По
этой причине в математических
исследованиях преимущественно используют
именно натуральные логарифмы. Они
нередко появляются при решении
дифференциальных
уравнений,
исследовании статистических зависимостей
(например, распределения
простых чисел)
и т. п.
Неопределенный
интеграл
от натурального логарифма легко найти
интегрированием
по частям:
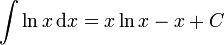
Разложение
в ряд
Тейлора
может быть представлено следующим
образом:
при
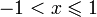 справедливо
равенство
справедливо
равенство
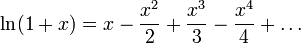
|
(1)
|
В
частности,
Формула
(1) не имеет большой практической ценности
из-за того, что ряд очень медленно
сходится и значение x
ограничено весьма узким диапазоном.
Однако нетрудно получить из неё более
удобную формулу:
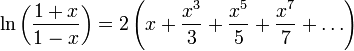
|
(2)
|
Этот
ряд сходится быстрее, а кроме того,
левая часть формулы теперь может
выразить логарифм любого положительного
числа.
73
74



75-76


77
Дифференци́руемая
фу́нкция в
математическом
анализе
— это функция, которая может быть хорошо
приближена линейной функцией.
Дифференцируемость является одним из
фундаментальных понятий в математике
и имеет большое число приложений как
внутри неё, так и в естественных науках,
широко использующих математический
аппарат.
Свойства Править
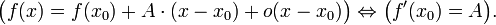
78


Инвариантность
формы дифференциала
Рассмотрим
сложную функцию y=f(u(x)).
Пусть функции
y=f(u),
u=u(x)
дифференцируемы, тогда

Таким
образом, если аргументом функции
является функция другого аргумента,
то форма дифференциала совпадает с
формой дифференциала (7),
когда аргументом функции является
независимая переменная. Это свойство
называется инвариантностью формы
дифференциала.
79
80 81


82
Сложная
функция – функция
от функции. Если z
– функция от у,
т.е. z(y),
а у,
в свою очередь, – функция от х,
т.е. у(х),
то функция f(x)
= z(y(x))
называется сложной
функцией
(или композицией,
или суперпозицией
функций) от
х.
В
такой функции х
– независимая,
а у
– промежуточная
переменная.
При этом сложная функция определена
для тех значений независимой переменной,
для которых значения промежуточной
функции у
входят в область определения функции
z(y).
Производная
дифференцируемой сложной функции равна
произведению производной данной функции
по промежуточному аргументу на
производную промежуточной функции по
независимому аргументу:
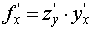 .
.
Эта
формула легко распространяется на
случай, когда у сложной функции имеется
два, три и более промежуточных аргументов
(«цепное правило»): если z
= f1(y1),
y1
= f2(y2),
…, yn-1
= fn(x),
то
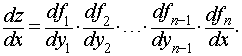
Дифференцирование сложной функции
[править]
Материал
из Википедии — свободной энциклопедии
Текущая
версия страницы пока не
проверялась
опытными участниками и может значительно
отличаться от версии,
проверенной 23 августа 2011; проверки
требуют 2
правки.


Текущая
версия страницы пока не
проверялась
опытными участниками и может значительно
отличаться от версии,
проверенной 23 августа 2011; проверки
требуют 2
правки.
Перейти
к: навигация,
поиск
Цепное
правило
(правило
дифференцирования сложной функции)
позволяет вычислить производную
композиции двух и более функций на
основе индивидуальных производных.
Если функция f имеет производную в точке
x0,
а функция g имеет производную в точке
y0
= f(x0),
то сложная функция h(x) = g(f(x)) также имеет
производную в
точке
x0.
Одномерный
случай
Пусть
даны функции, определённые в окрестностях
на числовой прямой,
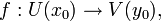 где
y0
= f(x0),
и
где
y0
= f(x0),
и
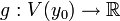 Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы:
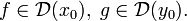 Тогда
их композиция также дифференцируема:
Тогда
их композиция также дифференцируема:
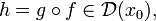 и
её производная имеет вид:
и
её производная имеет вид:
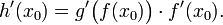
[править]
Замечание
[править]
Инвариантность
формы первого дифференциала
Дифференциал
функции z
= g(y)
в точке y0
имеет вид:
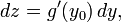
где
dy —
дифференциал тождественного отображения
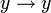 :
:
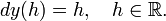
Пусть
теперь
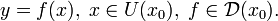 Тогда
Тогда
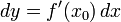 ,
и согласно цепному правилу:
,
и согласно цепному правилу:
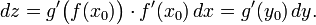
Таким
образом, форма первого дифференциала
остаётся одной и той же вне зависимости
от того, является ли переменная функцией
или нет.
[править]
Пример
Пусть
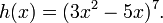 Тогда
функция
Тогда
функция
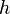 может
быть записана в виде композиции
может
быть записана в виде композиции
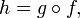 где
где
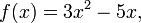
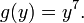
Дифференцируя
эти функции отдельно:
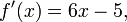
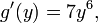
получаем
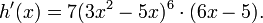
[править]
Многомерный
случай
Пусть
даны функции
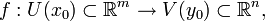 где
y0
= f(x0),
и
где
y0
= f(x0),
и
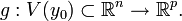 Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы:
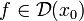 и
и
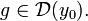 Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид
Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид
dh(x0)
= dg(y0)
* df(x0).
В
частности, матрица Якоби функции h
является произведением матриц Якоби
функций g
и f:
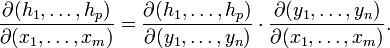
[править]
Следствия
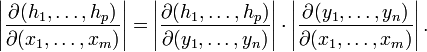
Для
частных производных сложной функции
справедливо
83
Определение
Функция
 является
обратной к функции
является
обратной к функции
 ,
если выполнены следующие тождества:
,
если выполнены следующие тождества:
f(g(y))
= y
для всех
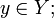
g(f(x))
= x
для всех
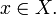
[править]
Существование
Чтобы
найти обратную функцию, нужно решить
уравнение
x
= F(y)
относительно y.
Если оно имеет более чем один корень,
то функции обратной к F
не существует. Таким образом, функция
f(x)
обратима на интервале (a;b)
тогда и только тогда, когда на этом
интервале она инъективна.
Для
непрерывной
функции
F(y)
выразить y
из уравнения x
− F(y)
= 0 возможно в
том и только том случае, когда функция
F(y)
монотонна (см. теорема
о неявной функции).
Тем не менее, непрерывную функцию всегда
можно обратить на промежутках её
монотонности. Например,
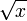 является
обратной функцией к x2
на
является
обратной функцией к x2
на
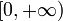 ,
хотя на промежутке
,
хотя на промежутке
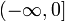 обратная
функция другая:
обратная
функция другая:
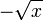 .
.
[Править] Примеры
[Править] Свойства

или
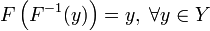 ,
,
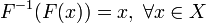 ,
,
или
короче
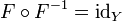 ,
,
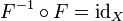 ,
,
где
 означает
композицию
функций,
а idX,idY —
тождественные
отображения
на X
и Y
соответственно.
означает
композицию
функций,
а idX,idY —
тождественные
отображения
на X
и Y
соответственно.
 .
.
[Править] Разложение в степенной ряд
Обратная
функция аналитической функции может
быть представлена в виде степенного
ряда:
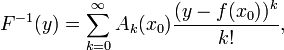
где
коэффициенты Ak
задаются рекурсивной формулой:

Теорема об обратной функции.
Теорема.
Если
функция f возрастает (или убывает) на
промежутке I, то она обратима. Обратная
к f функция g, определенная в области
значений f, также является возрастающей
(соответственно убывающей).
Доказательство.
Положим для определенности, что
функция f возрастающая. Обратимость
функции f — очевидное следствие теоремы
о корне . Поэтому остается доказать,
что функция g, обратная к f, возрастает
на множестве E(f).
Пусть x1
и x2
— произвольные значения из Е (f), такие,
что x2>
x1.
и пусть y1=g(x1),
y2=g(x2).
По определению обратной функции x1=f(y1)
и x2=f(y2).
Воспользовавшись
тем условием, что f — возрастающая
функция, находим, что допущение y1
≥ y2
приводит к выводу f (y1)≥f(y2),
т. е. x1≥
x2.
Это противоречит предположению x2>
x1.
Поэтому y2>
y1
, т. е. из условия x2>
x1
следует, что g (x2)>g
(x1).
Производная
обратной функции
[править]
Материал
из Википедии — свободной энциклопедии
Текущая
версия
(не проверялась)
Перейти
к: навигация,
поиск
Пусть
 -
дифференцируемая
функция
от аргумента x в некотором интервале
.
Если в уравнении
y
считать аргументом, а x - функцией, то
возникает новая функция
-
дифференцируемая
функция
от аргумента x в некотором интервале
.
Если в уравнении
y
считать аргументом, а x - функцией, то
возникает новая функция
 ,
где
,
где
 -
функция
обратная данной.
-
функция
обратная данной.
Теорема (о дифференцировании обратной функции)
Для
дифференцируемой функции с производной,
отличной от нуля, производная
обратной функции
равна обратной величине производной
данной функции, т.е
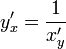
Примеры
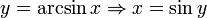 ,
,
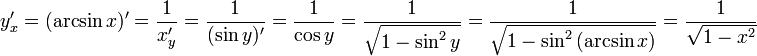
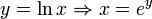 ,
,
 [1]
[1]
 .
.
84
Дифференцирование функций заданных параметрически
До
сих пор функция записывалась в явном
виде y= f(x) и в неявном F(x,y)=0. Но существует
еще третий вид аналитического
представления функции – это представление
её в па раметрической форме в виде двух
уравнений
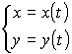
где
t – вспомогательная переменная,
называемая параметром.
Заметим,
что функция может быть представлена в
параметрической форме различными
способами.
Например, функция,
записанная в неявном виде x2 + y2 = 1 может
быть представлена в явном виде:
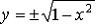 и
в параметрической форм е:
и
в параметрической форм е:
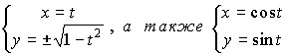
Заметим,
что x2 + y2 = 1 есть уравнение окружности
единичного радиуса с центром в начале
координат.
В первом параметрическом
представлении уравнения x2 + y2 = 1 параметр
t изменяется от – 1 до +1 и равен абциссе
подвижной точки окружности, во втором
случае параметр t изменяется от 0 до 2p
и равен углу, образованному радиусом
подвижной точки и осью Ox.
Если
функция задана в явном виде y=f(x), то
всегда можно записать её в неявном виде
y-f(x)=0, а также в параметрической форме
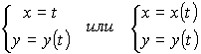
От
вида F(x,y)=0 не всегда возможно перейти
к виду y=f(x) или x=φ (y), так как уравнение
F(x,y)=0 может оказаться неразреш имым
относительно y или x .
Лего
перейти от параметрического представления
функции к уравнению вида y=f(x). Для этого
из первого уравнения x=x(t) нужно найти
t=t(x), если конечно это возможно , и
подставить его во второе уравнение
y=y(t)
y=y[t(x)]=f(x)
От
параметрического представления функции
к уравнению вида F(x,y)=0 можно прийти
путем исключения параметра t, если это
возможно.
Уравнения y=f(x) и F(x,
y)=0 служат различными аналитическими
представлениями одной и той же функции
F[x, f(x)]=0.
Параметрические
уравнения
и
уравнение F(x, y)=0 представляют одну и ту
же функцию, если F(x(t), y(t))=0.
Наконец,
параметрические уравнения определяют
ту же функцию, что и уравнение y=f(x), если
y(t)=f
[ x(t) ].
Найдем
производную функции y по x в случае,
когда она задана в параметрическом
виде. Для этого будем рассматривать t
как функцию от x. То есть t=t(x). Тогда
y=y[t(x)].
Продифференцируем y как
сложную функцию от x, т.е. по формуле
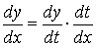
и
применим формулу, связывающую производные
обратных функций:
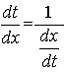
Введя
обозначения
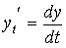 ,
,
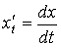
получим
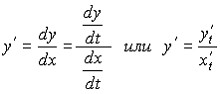
Пример.
Теперь
найдем вторую производную от функции,
заданной в параметрической форме. Из
предидущего уравнения и определения
второй производной следует, что
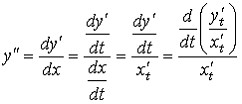
но
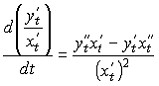
Следовательно
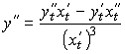
где
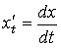
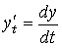

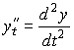
85
36. Логарифмическое дифференцирование.
Логарифмическое
дифференцирование -
в некоторых случаях целесообразнее
функцию
сначала прологарифмировать, а результат
продифференцировать.
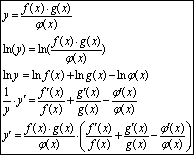
Однако
производные степенных функций находят
только логарифмическим
дифференцированием.
Производная
степенно-показательной функции равна
сумме производно
показательной
функции, при условии U=const, и производной
степенной функции,
при
условии V=const.
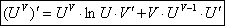
86
Производные
и дифференциалы высших порядков.
Пусть
функция f(x)-
дифференцируема на некотором интервале.
Тогда, дифференцируя ее, получаем первую
производную
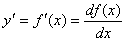
Если
найти производную функции f(x),
получим вторую
производную функции
f(x).
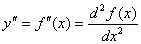
т.е.
y
= (y)
или
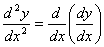 .
.
Этот
процесс можно продолжить и далее, находя
производные степени n.
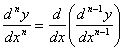 .
.
Общие
правила нахождения высших производных.
Если
функции u
= f(x)
и v
= g(x)
дифференцируемы, то
1)
(Сu)(n) =
Cu(n);
2)
(u
v)(n)
= u(n)
v(n);
3)
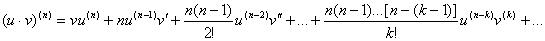
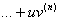 .
.
Это
выражение называется формулой
Лейбница.
Также
по формуле dny
= f(n)(x)dxn
может быть найден дифференциал n-
го порядка.
87
Производная
степенной функции.
Найдем производные
от некоторых простейших функций.
Пусть
 .
Имеем
.
Имеем
 ,
,
т. е.
производная
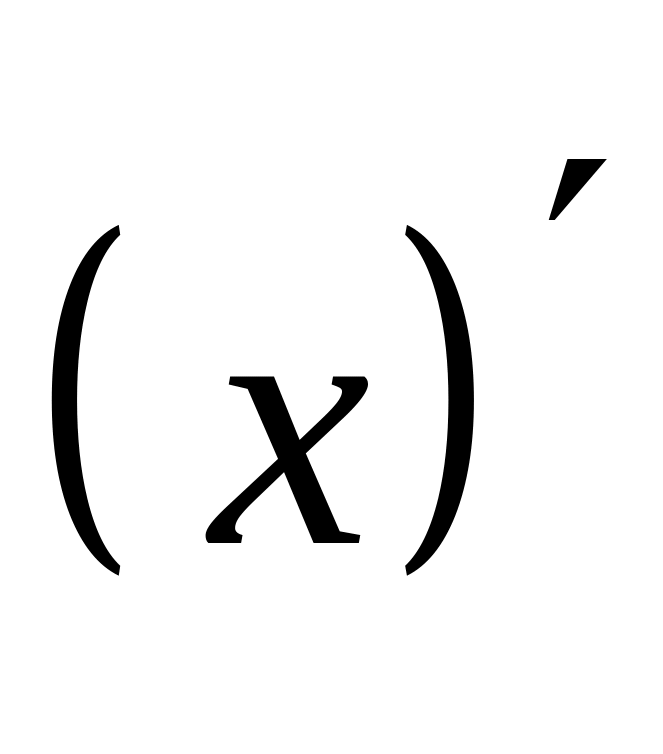 есть постоянная величина, равная 1. Это
очевидно, ибо
- линейная функция и скорость ее изменения
постоянна.
есть постоянная величина, равная 1. Это
очевидно, ибо
- линейная функция и скорость ее изменения
постоянна.
Если
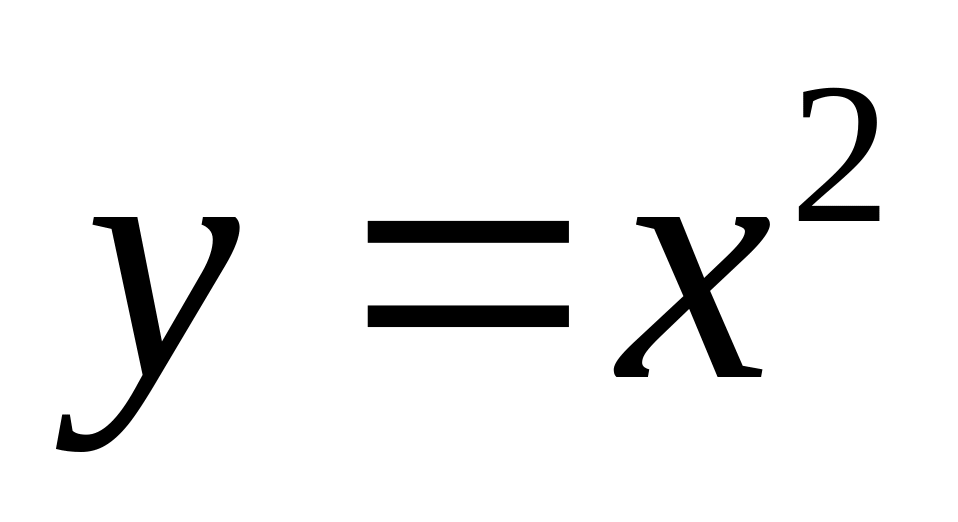 ,
то
,
то
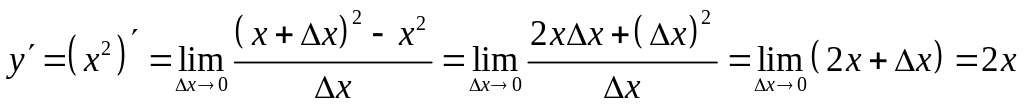 .
.
Пусть
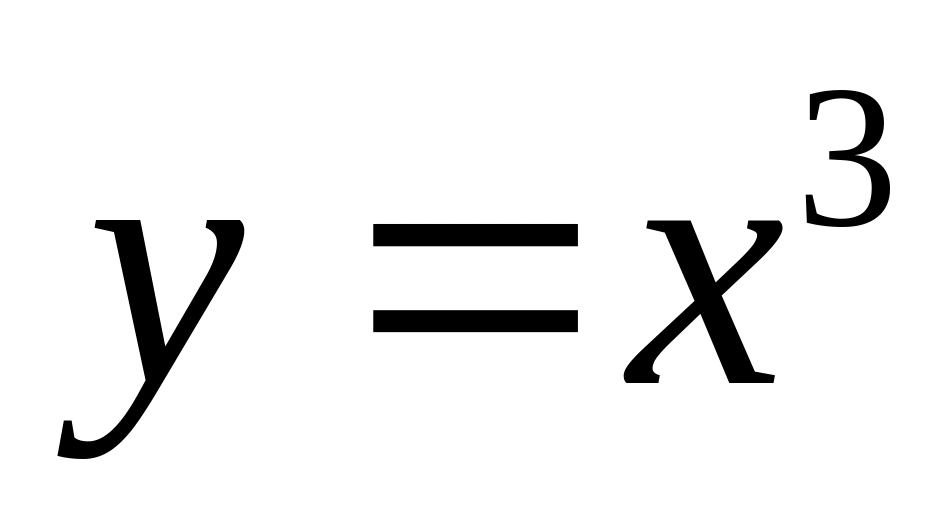 ,
тогда
,
тогда
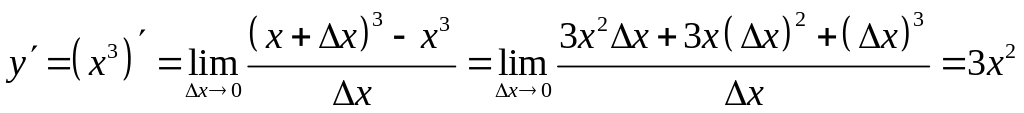 .
.
Легко
заметить закономерность в выражениях
производных от степенной функции
 при
при
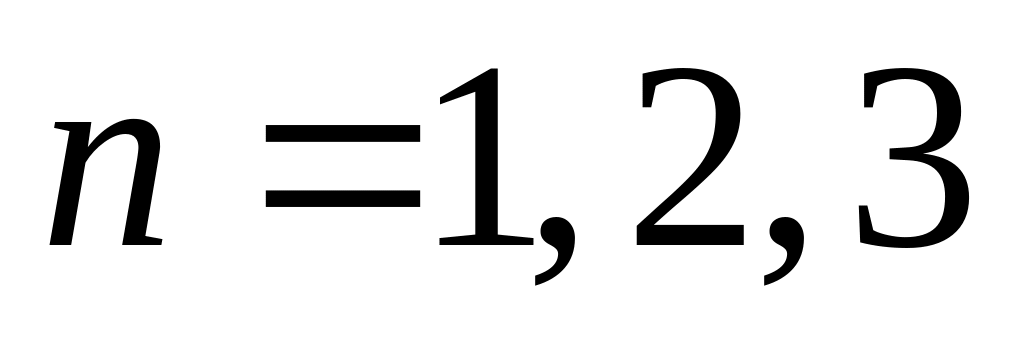 .
Докажем, что и вообще производная от
при любом целом положительном показателе
.
Докажем, что и вообще производная от
при любом целом положительном показателе
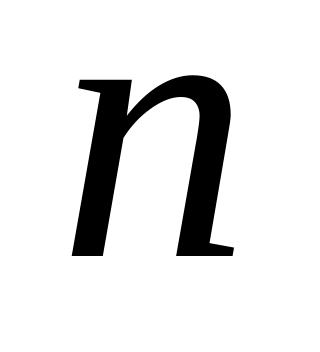 равна
равна
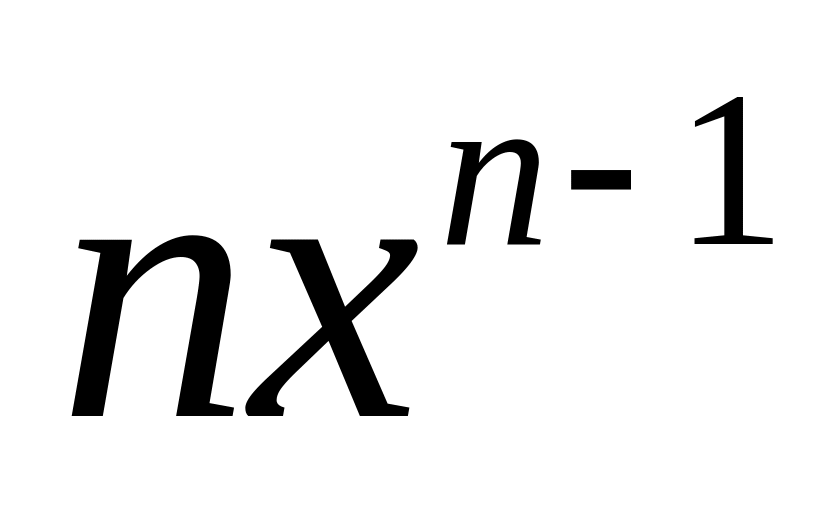 .
.
Имеем
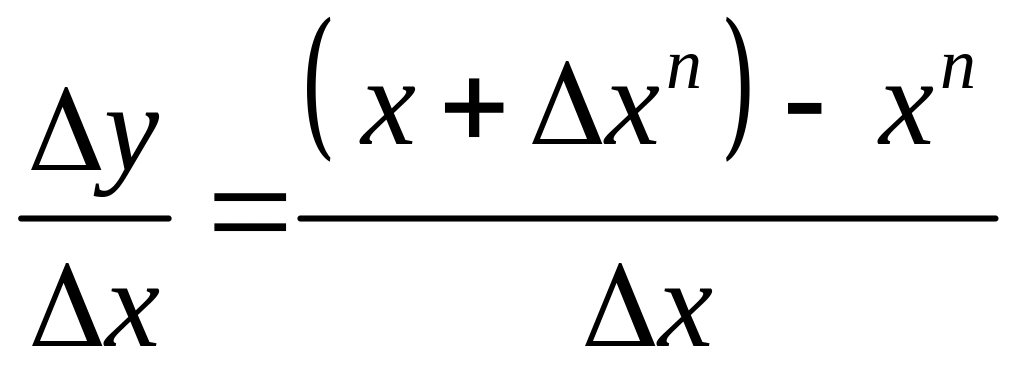 .
.
Выражение,
стоящее в числителе, преобразуем по
формуле бинома Ньютона:
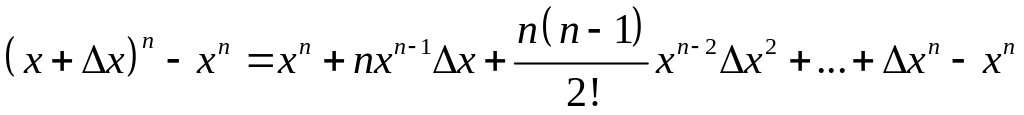 .
.
Значит,
 .
.
В
правой части последнего равенства
стоит сумма
слагаемых, первое из которых не зависит
от
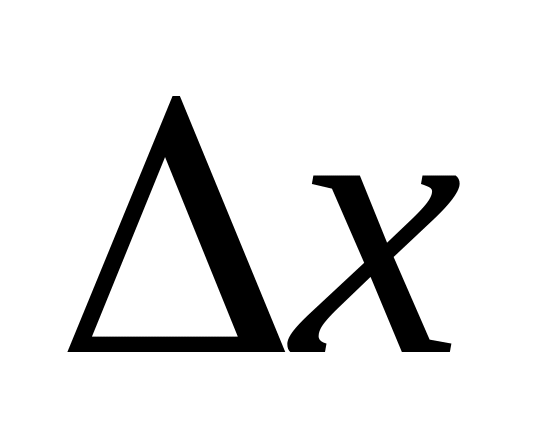 ,
а остальные стремятся к нулю
вместе с
.
Поэтому
,
а остальные стремятся к нулю
вместе с
.
Поэтому
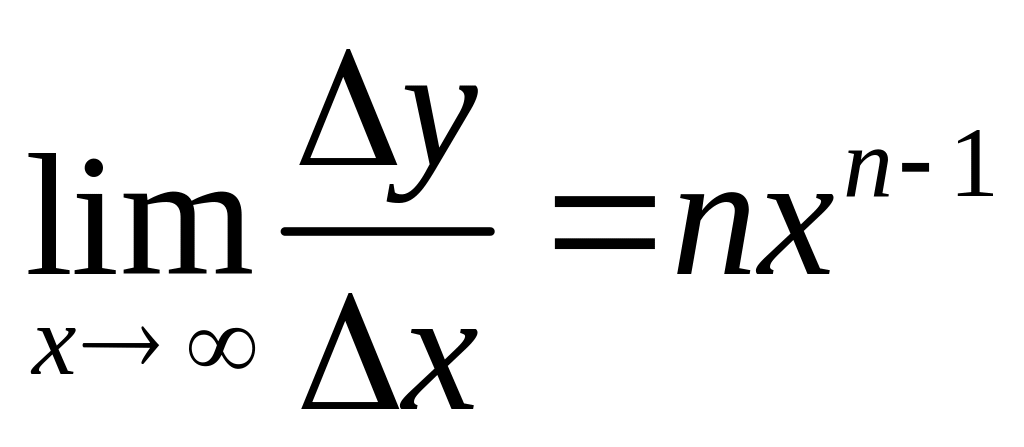 .
.
Итак, степенная
функция
при целом положительном
имеет производную, равную
:
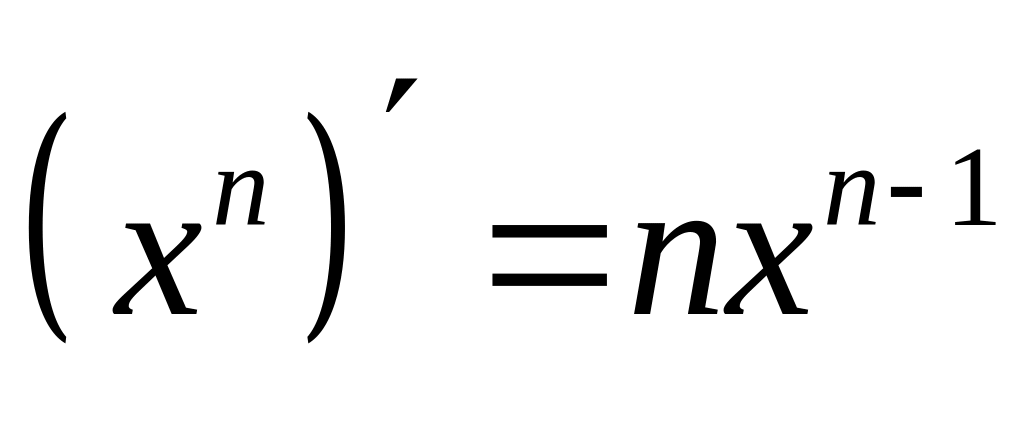 .
.
При
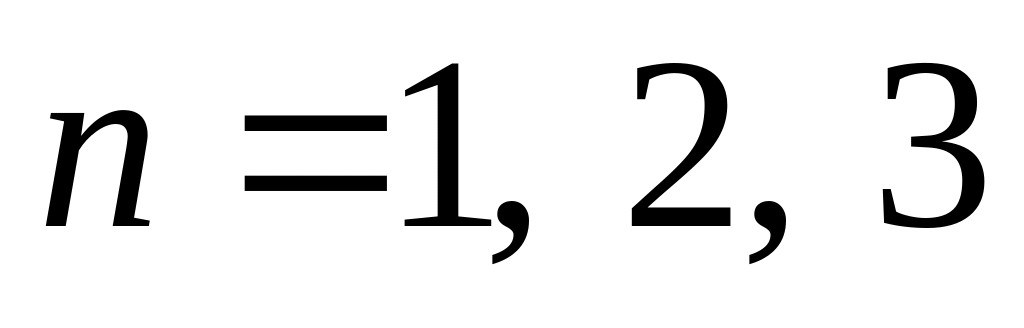 из найденной общей формулы следуют
формулы, выведенные выше.
из найденной общей формулы следуют
формулы, выведенные выше.
Этот
результат верен для любого показателя
,
например:
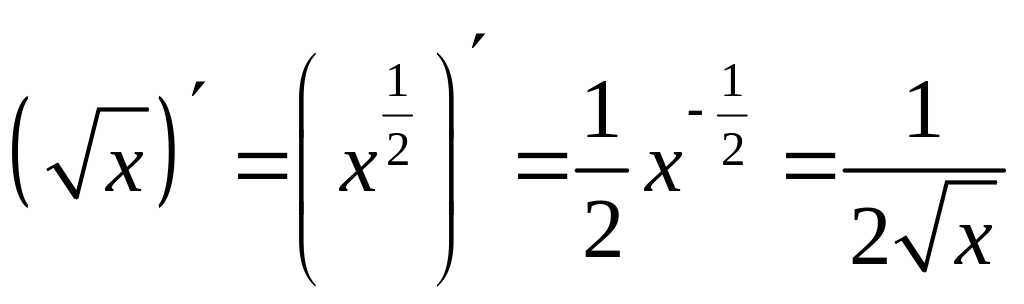 .
.
Рассмотрим теперь
отдельно производную от постоянной
величины
 .
.
Так
как эта функция не изменяется с изменением
независимой переменной, то
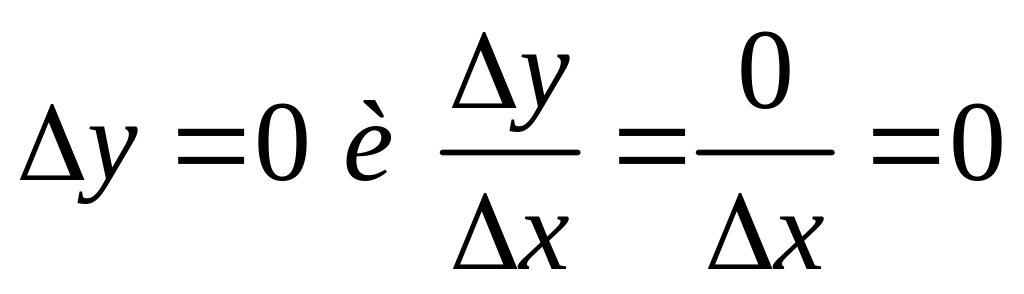 .
Следовательно,
.
Следовательно,
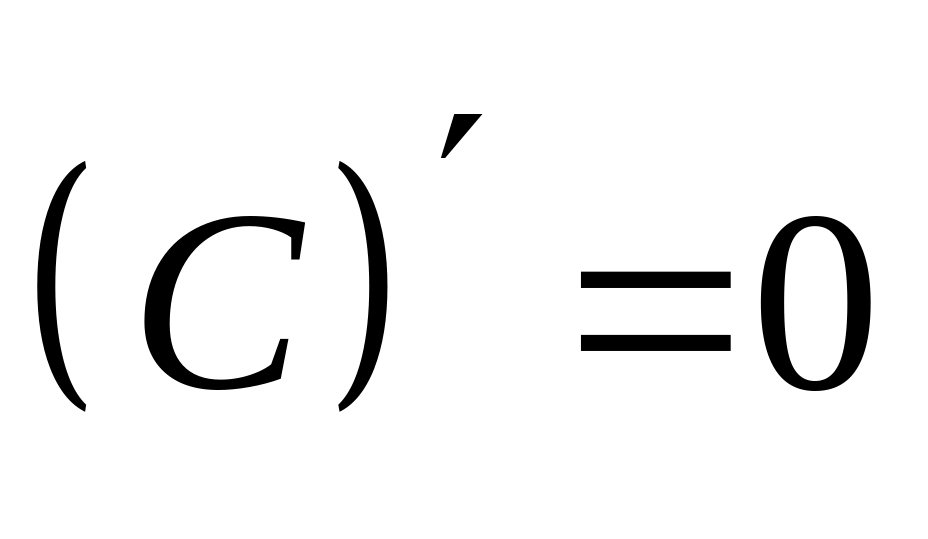 ,
,
т.
е.
производная
постоянной равна нулю.
88
Правила отыскания производных показательных и логарифмических функций.
Формула
производной
показательной функции:
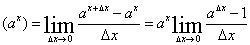 .
.
Чтобы
оценить, чему равен
 ,
посмотрим, какой смысл имеет выражение
,
посмотрим, какой смысл имеет выражение
 ,
стоящее под знаком этого предела.
,
стоящее под знаком этого предела.
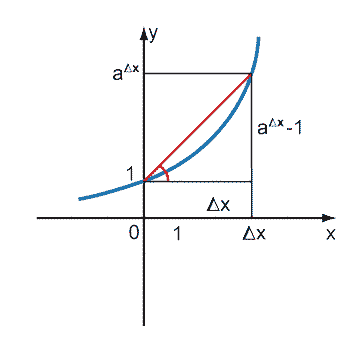
Для
этого отложим приращение
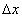 от
нуля. Разность
от
нуля. Разность
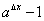 окажется
приращением функции в точке 0.
Следовательно, отношение
окажется
тангенсом угла наклона секущей,
проходящей через точку графика с
абсциссой 0.
Но это значит, что
-
это тангенс угла наклона касательной,
проходящей через точку графика с
абсциссой 0.
Мы доказали, что
-
это производная функции
окажется
приращением функции в точке 0.
Следовательно, отношение
окажется
тангенсом угла наклона секущей,
проходящей через точку графика с
абсциссой 0.
Но это значит, что
-
это тангенс угла наклона касательной,
проходящей через точку графика с
абсциссой 0.
Мы доказали, что
-
это производная функции
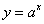 в
точке 0:
в
точке 0:
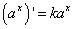 ,
,
где
k
- производная функции в точке нуль.
Отсюда сразу получается формула для
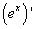 .
.
Ведь число е
- основание логарифмической функции,
график которой пересекает ось абсцисс
под углом 45°.
Но тогда график обратной функции
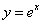 пересекает
под углом 45°
ось ординат, а следовательно, и ось
абсцисс. То есть производная функции
в
нуле равна 1.
пересекает
под углом 45°
ось ординат, а следовательно, и ось
абсцисс. То есть производная функции
в
нуле равна 1.
Отсюда
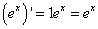 .
.
По
формуле производной обратной функции
получаем производную
натурального логарифма:
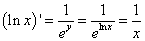 .
.
Теперь
получаем производную логарифма с
произвольным основанием:
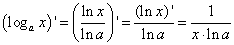 .
.
И,
наконец, получаем производную
показательной функции
с произвольным основанием:
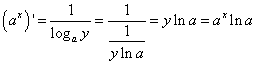 .
.
89
Производные
тригонометрических функций
Производные шести
тригонометрических функций и,
соответственно, шести обратных
тригонометрических функций определяются
следующими формулами (рядом указана
область определения каждой функции):
В приведенных ниже
примерах мы предполагаем, что читатель
(или если кто предпочитает - "пользователь")
знаком с основными тригонометрическими
формулами.
90
Производные обратных тригонометрических функций
Добавил
admin | Рубрики: Дифференциальное
исчисление
Основные
формулы:
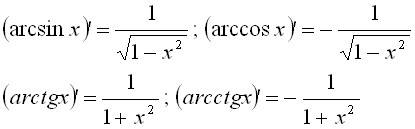
Для
сложных функций:
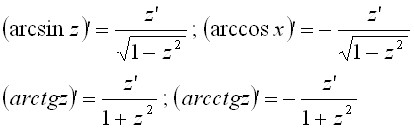
Пусть
 имеет
обратную ф-ию на
имеет
обратную ф-ию на
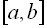
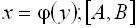
Рассмотрим
отнош.
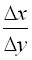
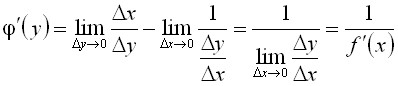
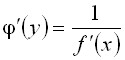
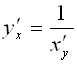
Рассмотрим
обратные тригонометрические ф-ии.
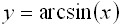
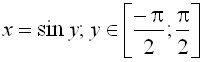

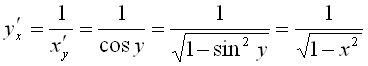
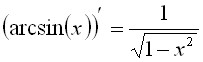
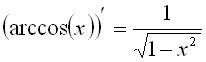

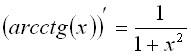
91
Теорема Ролля
Пусть
функция f
(x)
непрерывна на [a,
b],
дифференцируема на (a,
b)
и на концах отрезка принимает равные
значения f(a)
= f(b).
Тогда существует точка c
(a,
b),
в которой f
' (c)
= 0.
Доказательство.
Так как функция f(x)
непрерывна на [a,
b],то
по свойству непрерывных функций она
достигает на этом отрезке максимальное
значение М и минимальное значение
m.
Возможны два случая:
максимум и минимум достигаются на
концах отрезка или что – либо (или
максимум, или минимум) попадает вовнутрь
интервала. В первом случае f
(x)
= const = M
= m.
Поэтому производная равна нулю f
' (c)
= 0 в любой точке отрезка [a,
b],
и теорема доказана.
Во
втором случае, так как f
(x)
дифференцируема в точке c,
из теоремы Ферма следует, что f
' (c)
= 0.
Геометрический смысл теоремы Ролля
Геометрически
теорема Ролля означает, что у графика
непрерывной на отрезке [a,
b]
и дифференцируемой внутри этого отрезка
функции, принимающей на его концах f(a)
= f(b)
равные значения, существует точка (c;
f(c)),
в которой касательная параллельна оси
Оx.
92
Теорема Лагранжа
Если
функция f(x)
непрерывна на замкнутом отрезке [a,
b],
дифференцируема внутри него, то
существует такая точка с
(a,
b),
что выполняется равенство
f(b)
− f(a)
= f
'(c)·(b
− a).
Д
о к а з а т е л ь с т в о. Составим уравнение
хорды,
проходящей через точки (a,
f(a)),
(b,
f(b))
y
= f(a)
+ Q·(x
- a),
где
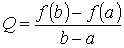 есть
угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
есть
угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
F(x)
= f(x)
− f(a)
− Q·(x
− a).
Очевидно,
что функция F(x)
удовлетворяет всем условиям теоремы
Ролля. Поэтому на интервале (a,
b)
найдётся такая точка с,
для которой F ' (c)
= 0. То есть F
' (c)
= f
' (c)
− Q
= 0. Откуда следует
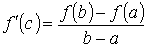 .
.
И,
наконец, f(b)
− f(a)
= f
'(c)·(b
− a).
Геометрический смысл теоремы Лагранжа
Величина
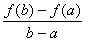 является
угловым коэффициентом секущей, проходящей
через точки M1
(a;
f(a))
и M2(b;
f
(b))
графика функции у
= f(x),
a f
' (c)
— угловой коэффициент касательной к
графику в точке (c;
f (c)).
Из теоремы Лагранжа следует, что
существует точка "c"
такая, что касательная к графику в точке
(c;
f(c))
параллельна секущей M1M2.
Таких точек может быть и несколько, но,
по крайней мере, одна всегда
существует.
Замечание.
Формула Лагранжа по структуре похожа
на формулу линеаризации
является
угловым коэффициентом секущей, проходящей
через точки M1
(a;
f(a))
и M2(b;
f
(b))
графика функции у
= f(x),
a f
' (c)
— угловой коэффициент касательной к
графику в точке (c;
f (c)).
Из теоремы Лагранжа следует, что
существует точка "c"
такая, что касательная к графику в точке
(c;
f(c))
параллельна секущей M1M2.
Таких точек может быть и несколько, но,
по крайней мере, одна всегда
существует.
Замечание.
Формула Лагранжа по структуре похожа
на формулу линеаризации
f
(x)
− f
(x0)
≈ f
'(x0)·(x
−x0).
Отличие
только лишь в выборе точки для подсчета
значения производной и в знаке равенства.
93
Теорема Коши
Пусть
функции f
(x)
и g(x)
непрерывны на [a,
b]
и дифференцируемы на (a,
b).
Пусть, кроме того, во всех точках
интервала (a,
b)
функция g(x)
имеет ненулевую производную g
' (x)
≠ 0. Тогда существует точка c
(a,
b),
такая, что справедлива формула
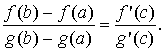
Д
о к а з а т е л ь с т в о. Покажем сначала,
что знаменатель левой части формулы
не обращается в ноль. Если допустить,
что g(b)
= g(a),
то по теореме Ролля для функции g(x)
найдется точка
(a,
b),
в которой g
' ()
= 0. А это противоречит условию, что g
' (x)
≠ 0 на (a,
b).
Рассмотрим
функцию
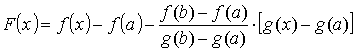 .
.
Функция
F(x)
на [a,
b]
удовлетворяет условиям теоремы Ролля:
F(x)
непрерывна на [a,
b],
дифференцируема на (a,
b),
и, кроме того, на концах интервала
принимает равные значения F(a)
= F(b)
= 0. По теореме Ролля для F(x)
существует точка c
(a,
b)
, такая ,что F
' (c)
= 0. Так как
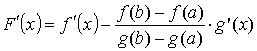 ,
,
то
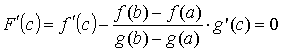 .
.
Откуда,
учитывая, что g '(c)
≠ 0, следует искомое соотношение.
94
Правило Лопиталя
На основе теоремы
Коши мы выведем правило, которое даст
нам мощный способ вычисления пределов
отношений двух бесконечно малых или
двух бесконечно больших величин.
Сформулируем его сначала для отношения
бесконечно малых.
Теорема
5.5 (Правило
Лопиталя) Пусть
функции
и
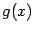 непрерывны
в некоторой окрестности
непрерывны
в некоторой окрестности
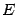 точки
точки
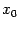 и
и
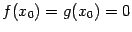 ,
то есть
,
то есть
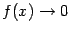 и
и
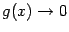 при
при
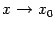 .
Предположим, что при
.
Предположим, что при
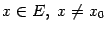 функции
и
имеют
производные
функции
и
имеют
производные
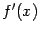 и
и
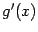 ,
причём существует предел отношения
этих производных:
,
причём существует предел отношения
этих производных:
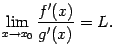
Тогда
предел отношения самих функций
и
тоже
существует и равен тому же числу
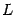 :
:
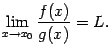
Доказательство.
Заметим, что из условия
 следует,
что оба односторонних предела также
равны
:
следует,
что оба односторонних предела также
равны
:
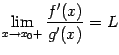 и
и
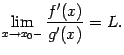
Пусть
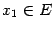 ,
,
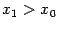 .
По теореме Коши, применённой к отрезку
.
По теореме Коши, применённой к отрезку
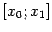 ,
получим тогда, с учётом того, что
,
получим тогда, с учётом того, что
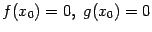 ,
,
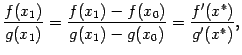
где
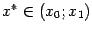 .
Перейдём теперь в этом равенстве к
пределу при
.
Перейдём теперь в этом равенстве к
пределу при
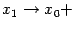 :
:
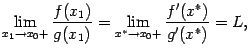
так
как, очевидно, при
имеем
также
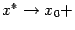 .
Теперь возьмём точку
.
Теперь возьмём точку
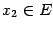 ,
,
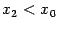 и
применим теорему Коши к отрезку
и
применим теорему Коши к отрезку
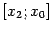 .
Получим
.
Получим

где
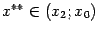 .
Переходя к пределу при
.
Переходя к пределу при
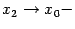 ,
получаем
,
получаем
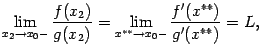
так
как при
имеем
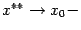 .
.
Итак, оба односторонних
предела отношения
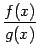 равны
.
На основании теоремы о связи односторонних
пределов с двусторонним получаем, что
равны
.
На основании теоремы о связи односторонних
пределов с двусторонним получаем, что
Замечание
5.5 При
доказательстве мы одновременно вывели
правило Лопиталя и для односторонних
пределов (то есть пределов при базах
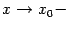 и
и
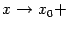 ):
если
и
бесконечно
малы при
и
существует предел
):
если
и
бесконечно
малы при
и
существует предел
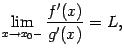
то
существует и предел
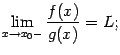
аналогичное
утверждение верно также для предела
справа.
Пример
5.3 Найдём
предел
 .
.
Этот предел
представляет собой предел отношения
двух бесконечно малых, поскольку
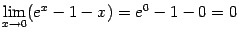 и
и
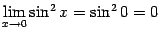 .
.
Заметим прежде
всего, что предел можно упростить,
заменив знаменатель
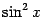 на
эквивалентную бесконечно малую:
на
эквивалентную бесконечно малую:
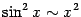 при
при
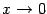 .
Получим:
.
Получим:
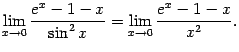
Числитель
упростить пока не удаётся, поскольку
правила вычисления пределов не позволяют
нам заменять на эквивалентные слагаемые
(а не множители). В предположении, что
предел существует, найдём вместо него
предел отношения производных, который,
в соответствии с доказанной теоремой,
равен исходному:
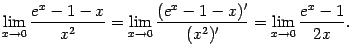
Получившийся
предел -- снова предел отношения
бесконечно малых, но его легко вычислить,
заменив числитель на эквивалентную
бесконечно малую:
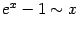 при
.
Получаем:
при
.
Получаем:
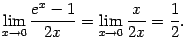
Итак,
получили, что предел отношения
производных, действительно, существует
и равен
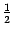 .
По правилу Лопиталя отсюда следует,
что исходный предел также существует
и равен тому же числу:
.
По правилу Лопиталя отсюда следует,
что исходный предел также существует
и равен тому же числу:
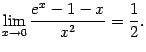
Следовательно,
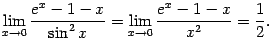
Замечание
5.6
Доказанное правило Лопиталя не означает,
что если предел отношения производных
не существует, то не существует и
исходный предел. Этот исходный предел
вполне может существовать, только его
нельзя найти при помощи применения
правила Лопиталя. Иными словами, правило
Лопиталя не
является универсальным
средством отыскания пределов отношения
двух бесконечно малых. Пример предела,
который нельзя отыскать с помощью
правила Лопиталя, мы сейчас приведём.
Пример
5.4
Рассмотрим предел
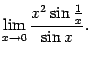 Его
легко вычислить, заметив, что величина
Его
легко вычислить, заметив, что величина
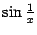 --
величина, локально ограниченная при
базе
,
а величина
--
величина, локально ограниченная при
базе
,
а величина
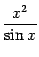 --
бесконечно малая:
--
бесконечно малая:
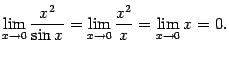
Следовательно,
их произведение -- бесконечно малая
величина, и
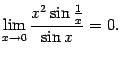
С
другой стороны, попробуем применить к
исходному пределу отношения двух
бесконечно малых
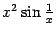 и
и
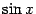 правило
Лопиталя и вычислить предел отношения
производных этих двух функций. Имеем:
правило
Лопиталя и вычислить предел отношения
производных этих двух функций. Имеем:
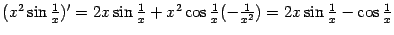 и
и
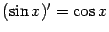 .
Составим отношение этих двух производных:
.
Составим отношение этих двух производных:
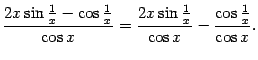
В
этом выражении первое слагаемое имеет,
очевидно, при
предел,
равный 0, а второе не имеет никакого
предела; следовательно, не имеет предела
и сумма.
Итак, исходное
отношение бесконечно малых имеет
предел, равный 0, в то время как отношение
производных этих бесконечно малых не
имеет никакого предела. Получаем, что
применение к данному примеру правила
Лопиталя не приводит к желаемому
вычислению предела.
Правило Лопиталя
действует не только при базах
,
,
,
но и при базах
 ,
,
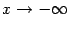 ,
,
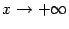 .
Докажем это.
.
Докажем это.
Теорема
5.6 (Правило
Лопиталя для
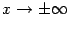 )
Пусть
и
--
функции, являющиеся бесконечно малыми
при базе
(или
,
или
)
и дифференцируемые на некотором луче
)
Пусть
и
--
функции, являющиеся бесконечно малыми
при базе
(или
,
или
)
и дифференцируемые на некотором луче
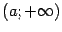 (или
(или
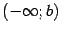 ,
или объединении лучей
,
или объединении лучей
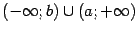 ,
соответственно). Тогда если существует
предел
,
соответственно). Тогда если существует
предел
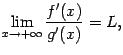
то
предел
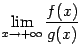 также
существует и равен тому же числу:
также
существует и равен тому же числу:
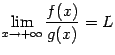
(аналогичные
утверждения справедливы и для баз
,
).
Доказательство.
Положим
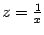 и
рассмотрим функции
и
рассмотрим функции
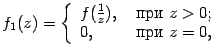 и
и
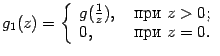 Тогда
функции
Тогда
функции
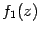 и
и
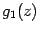 непрерывны
на отрезке
непрерывны
на отрезке
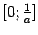 и
дифференцируемы при
и
дифференцируемы при
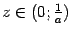 .
При этом
.
При этом
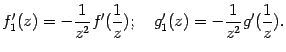
К
бесконечно малым при
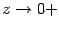 величинам
и
можно
применить правило Лопиталя ( теорема
5.5 для
предела справа, см. замечание
5.5):
величинам
и
можно
применить правило Лопиталя ( теорема
5.5 для
предела справа, см. замечание
5.5):
Распространим
теперь правило Лопиталя на случай,
когда функции
и
являются
бесконечно большими величинами при
данной базе (о бесконечно больших
величинах см. раздел 2.7).
Теорема
5.7 (Правило
Лопиталя для отношения бесконечно
больших) Пусть
 и
и
 при
и
в некоторой проколотой окрестности
при
и
в некоторой проколотой окрестности
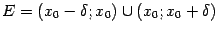 ,
,
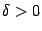 ,
существуют производные
и
.
Тогда, если существует предел отношения
этих производных
,
существуют производные
и
.
Тогда, если существует предел отношения
этих производных
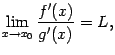
то
существует и предел отношения самих
функций, равный тому же числу:
Доказательство.
За полным доказательством этого
утверждения мы отсылаем к книгам
[Никольский С. М.,
Курс
математического анализа. Том 1. --
М.: Наука, 1990. -- С. 200 - 201] или
[Смирнов В. И.,
Курс высшей
математики. Том 1. --
М.: Наука, 1974. -- С. 157 - 158]. Здесь
же мы докажем, что оба предела совпадают,
в предположении, что второй из них
существует и оба не равны 0. Итак, пусть
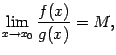
где
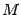 --
некоторое число. Докажем, что тогда
--
некоторое число. Докажем, что тогда
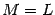 .
.
Рассмотрим
вспомогательные функции
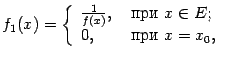 и
и
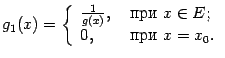
Тогда функции
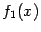 и
и
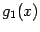 --
бесконечно малые при
,
непрерывные при
--
бесконечно малые при
,
непрерывные при
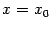 ;
их производные таковы:
;
их производные таковы:

Заметим
теперь, что при
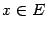
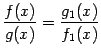
|
(5.3)
|
и
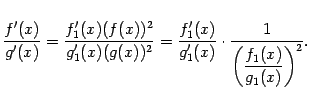
|
(5.4)
|
Из
равенства (5.3)
получаем, что
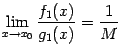 .
Переходя к пределу в равенстве (5.4),
получаем:
.
Переходя к пределу в равенстве (5.4),
получаем:
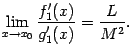
С
другой стороны, применяя правило
Лопиталя ( теорема
5.5) к
бесконечно малым функциям
и
,
получим:
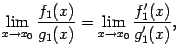
откуда
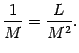
Из
этого равенства следует, что
,
что и требовалось доказать.
Замечание
5.7 Немного
изменив доказательство, мы получим,
что правило Лопиталя для отношения
двух бесконечно больших верно для
односторонних пределов (при базах
и
);
сделав замену
,
выведем, что оно верно для пределов при
базах
,
и
(аналогично
тому, как теорема
5.6 была
выведена из теоремы
5.5).
Замечание
5.8 Как и
в основном случае отношения двух
бесконечно малых при
,
все остальные варианты правила Лопиталя
не универсальны: если предел отношения
производных не существует, то это ещё
не означает, что нет предела отношения
исходных величин.
Приведём ещё один
пример, иллюстрирующий это важное
замечание.
Пример
5.5
Рассмотрим при
две
бесконечно больших:
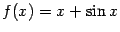 и
и
 .
Предел их отношения, очевидно, существует:
.
Предел их отношения, очевидно, существует:
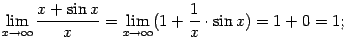
в
то же время отношение производных даёт
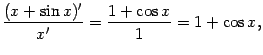
а
эта функция не имеет никакого предела
при
.
Следовательно, для вычисления предела
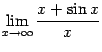
правило
Лопиталя неприменимо.
Несмотря на свою
неуниверсальность, правило Лопиталя
служит весьма мощным средством нахождения
сложных пределов. При этом иной раз
приходится применять это правило много
раз подряд, пока не получим предел,
значение которого либо очевидно, либо
может быть вычислено каким-либо способом,
изученным нами ранее (например, с помощью
замены на эквивалентные бесконечно
малые).
Пример
5.6 Найдём
предел
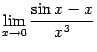 .
(Это предел отношения двух бесконечно
малых. Заметим, что
не
является множителем, так что его нельзя
заменить на эквивалентную величину
.
(Это предел отношения двух бесконечно
малых. Заметим, что
не
является множителем, так что его нельзя
заменить на эквивалентную величину
 ;
если бы мы всё же сделали это, то сразу
получили бы в числителе 0, и "ответ"
равнялся бы 0.) Применим правило Лопиталя
и получим, что
;
если бы мы всё же сделали это, то сразу
получили бы в числителе 0, и "ответ"
равнялся бы 0.) Применим правило Лопиталя
и получим, что
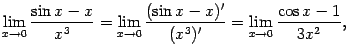
в
предположении, что последний предел
существует. Этот последний предел можно
найти, заметив, что
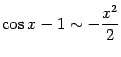 при
,
и заменив числитель. Однако можно пойти
и другим путём. Мы снова получили
отношение двух бесконечно малых, к
которому снова применим правило
Лопиталя:
при
,
и заменив числитель. Однако можно пойти
и другим путём. Мы снова получили
отношение двух бесконечно малых, к
которому снова применим правило
Лопиталя:
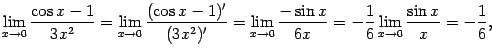
поскольку
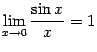 (это
первый замечательный предел).
(это
первый замечательный предел).
Итак, обоснование
результата таково:
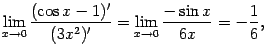
откуда
по теореме
5.5
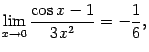
то
есть
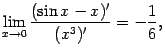
откуда,
в свою очередь, снова по теореме
5.5
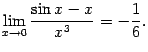
95
96
Функция
y=f(x)
называется возрастающей
(убывающей)
в некотором интервале, если при x1<
x2
выполняется неравенство f(x1)
< f
(x2)
(f(x1)
> f(x2)).
Если
дифференцируемая функция y
= f(x)
на отрезке [a,
b]
возрастает (убывает), то ее производная
на этом отрезке f
(x)
0 (f
(x)
0).
Точка
xо
называется
точкой
локального максимума
(минимума)
функции f(x),
если существует окрестность точки xо,
для всех точек которой верно неравенство
f(x)
f(xо)
(f(x)
f(xо)).
Точки
максимума и минимума называются точками
экстремума,
а значения функции в этих точках - ее
экстремумами.
Необходимые
условия экстремума.
Если точка xо
является точкой экстремума функции
f(x),
то либо f
(xо)
= 0, либо f
(xо)
не существует. Такие точки называют
критическими,
причем сама функция в критической точке
определена. Экстремумы функции следует
искать среди ее критических точек.
Первое
достаточное условие.
Пусть xо
- критическая точка. Если f
(x)
при переходе через точку xо
меняет знак плюс на минус, то в точке
xо
функция имеет максимум, в противном
случае - минимум. Если при переходе
через критическую точку производная
не меняет знак, то в точке xо
экстремума нет.
Второе
достаточное условие.
Пусть функция f(x)
имеет производную
f
(x)
в окрестности точки xо
и вторую
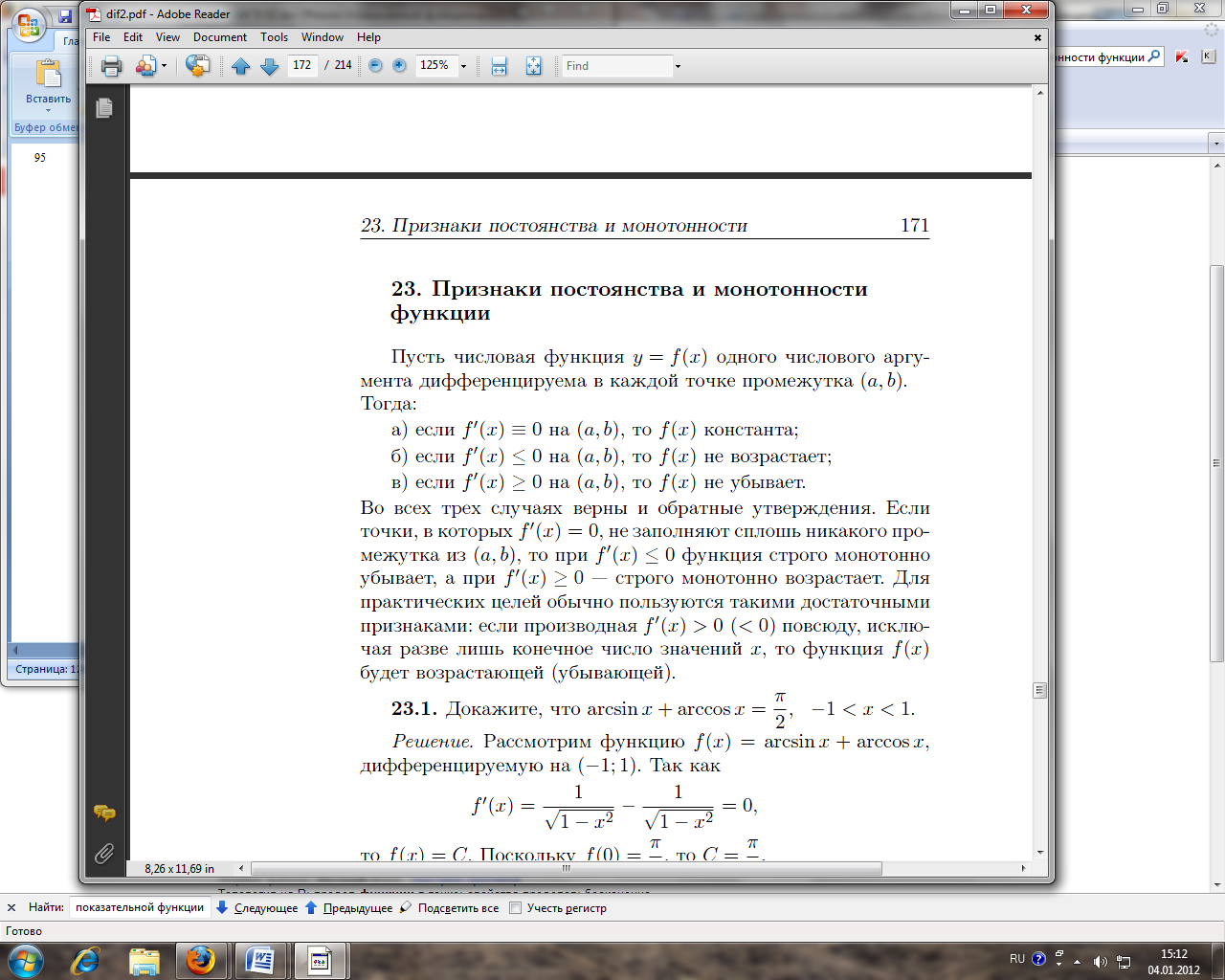
производную
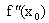 в
самой точке xо.
Если f
(xо)
= 0,
>0
(
<0),
то точка xо
является
точкой локального минимума (максимума)
функции f(x).
Если же
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
в
самой точке xо.
Если f
(xо)
= 0,
>0
(
<0),
то точка xо
является
точкой локального минимума (максимума)
функции f(x).
Если же
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
На
отрезке [a,b]
функция y
= f(x)
может достигать наименьшего или
наибольшего значения либо в критических
точках, либо на концах отрезка [a,b].
Достаточные
условия существования экстремума
Теорема
21.
Пусть
функция y
= f(x)
непрерывна на всем интервале (a,
b),
дифференцируема на (a,
b), кроме,
быть может, числа x0 (a,b),
причем точка (x0,
f(x0))
является критической точкой графика
функции f.
Тогда, если при переходе через x0
производная меняет знак с плюса на
минус (с минуса на плюс), то f'(x0)
– максимум (минимум) функции f.
(a,b),
причем точка (x0,
f(x0))
является критической точкой графика
функции f.
Тогда, если при переходе через x0
производная меняет знак с плюса на
минус (с минуса на плюс), то f'(x0)
– максимум (минимум) функции f.
Доказательство.
Пусть
при переходе через x0
производная функции f
меняет знак с плюса на минус. Рассмотрим
x = x0
+ Δx
(a,b)
число . Если Δx
> 0, то,
воспользовавшись теоремой Лагранжа,
имеем
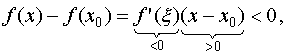
где
 ,
если Δx <
0, то
,
если Δx <
0, то
где
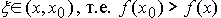
Доказано,
что значение f(x0)
– максимум функции f.
Аналогично доказывается, что если при
переходе через x0
производная меняет знак с минуса на
плюс, то
f(x0)
– минимум функции f.
97
Экстремум
функции. Необходимое условие существования
экстремума
Пусть
функция y
= f(x)
непрерывна на (a,
b) и пусть
x0
(a,b)
Определение
5. Значение f(x0)
называется максимумом
(минимумом)
функции f,
если в некоторой малой окрестности
числа x0
значение f(x0)
является наибольшим (наименьшим), т.е.
для любого числа x
из этой окрестности f(x0)
> f(x)
(f(x0)
< f(x)).
Максимум и минимум функции f
называется экстремумом
функции f.
Теорема
20.
Пусть
функция y
= f(x)
дифференцируема на (a,
b), число
x0
(a,b)
и f(x0)
является экстремумом функции f.
Тогда f'(x0)
= 0.
Доказательство.
Пусть
f(x0)
является
максимумом функции f,
тогда
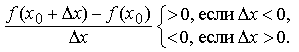
Переходя
к пределу, получаем
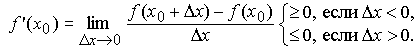
Так
как по условию теоремы при x
= x0
производная функции f
существует, то f'(x0)
= 0.
Аналогично доказывается, что если f(x0)
является
минимумом функции f
, то f'(x0)
= 0.
Теорема
доказана.
Обратное
для теоремы 20 утверждение неверно, т.е.
если f'(x0)
= 0, то
f(x0)
может не быть экстремумом функции f.
Например, функция y
= x3
имеет производную y'
= 3x2,
которая при x
= 0 равна
нулю. Однако, как видно из рис. 3, при
x = 0 функция
y = x3
не имеет экстремума.
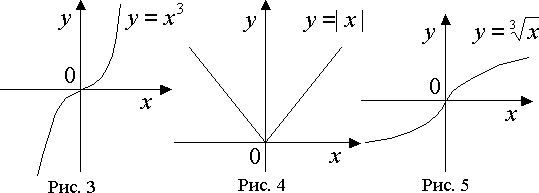
Если
окажется, что при x
= x0непрерывная
функция y
= f(x) не
дифференцируема, то также нельзя
однозначно сказать, будет значение
f(x0)
экстремумом функции f
или нет.
Например,
функции y
= | x |, y
= 3√x
не дифференцируемы при x
= 0. Однако
функция y
= | x | при
x = 0 имеет
экстремум (рис. 4), а функция y
= 3√x
при x = 0
экстремума не имеет (рис. 5).
98
99

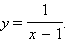 Она
разрывна в точке x0 = 1,
так как не существует в этой точке.
Она
разрывна в точке x0 = 1,
так как не существует в этой точке.
![]() непрерывна
в ней при условии, что g (x0) ≠ 0.
непрерывна
в ней при условии, что g (x0) ≠ 0.![]() еорема
Вейерштрасса.
Если функция f (x)
непрерывна на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.
еорема
Вейерштрасса.
Если функция f (x)
непрерывна на отрезке [a; b],
то она ограничена на этом отрезке и
достигает своего наибольшего и
наименьшего значения.
![]() (и
возможно, не одна) такая, что f (x) = y.
(и
возможно, не одна) такая, что f (x) = y.![]() и
и
![]() такие,
что:
такие,
что:![]() ;
;![]() и
и
![]() конечны
на интервале
конечны
на интервале
![]() ;
;![]() ;
;![]() ,
где
,
где
![]()
![]()
![]() равна
как раз необходимому числу.
равна
как раз необходимому числу.![]() и
и
![]() .
Пусть
.
Пусть![]()
![]() )
и достигаются (существуют
)
и достигаются (существуют
![]() такие,
что
такие,
что
![]() ).
).![]() ,
предел которой лежит в A.
,
предел которой лежит в A.![]() ,
поэтому, применяя предельный
переход,
получаем
,
поэтому, применяя предельный
переход,
получаем
![]() и
в силу непрерывности функции существует
точка x0
такая, что
и
в силу непрерывности функции существует
точка x0
такая, что
![]() и,
следовательно M
= f(x0).
и,
следовательно M
= f(x0).![]()
![]() и
и
![]()
![]() и
и
![]()
![]() и
компактное
подмножество
и
компактное
подмножество
![]() .
Пусть дана непрерывная функция
.
Пусть дана непрерывная функция
![]() .
Тогда
.
Тогда![]()
![]()
![]()

![]() и
и
![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.![]() .
Отложим этот угол на единичной окружности
(R
= 1).
.
Отложим этот угол на единичной окружности
(R
= 1).![]() (1)
(1)![]()
![]()
![]()
![]() :
| LA
| = tgx)
:
| LA
| = tgx)![]()
![]() :
:![]()
![]()
![]()
![]()
![]()
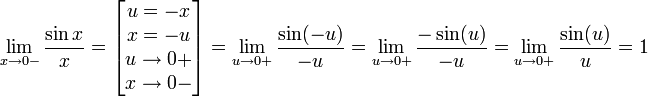
![]()
![]()
![]()
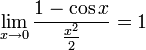
![]() или
или
![]()
![]() Докажем
вначале теорему для случая последовательности
Докажем
вначале теорему для случая последовательности
![]()
![]()
![]() ,
получим:
,
получим:![]()
![]() (1)
(1)![]() убывает,
поэтому величины
убывает,
поэтому величины
![]() возрастают.
Поэтому последовательность
возрастают.
Поэтому последовательность
![]() —
возрастающая,
при этом
—
возрастающая,
при этом![]() (2).
(2).![]()
![]() .
.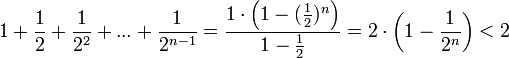 .
.![]() (3).
(3).![]() выполняются
неравенства (2) и (3):
выполняются
неравенства (2) и (3):
![]() .
.![]() монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е.
монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е.
![]()
![]()
![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами:
![]() ,
где
,
где
![]() —
это целая часть x.
—
это целая часть x.![]() ,
поэтому
,
поэтому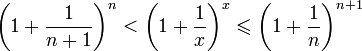 .
.![]() .
Поэтому, согласно пределу
,
имеем:
.
Поэтому, согласно пределу
,
имеем: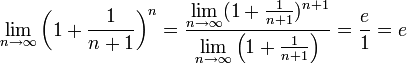
![]() .
.![]() .
.![]() .
Сделаем подстановку −
x
= t,
тогда
.
Сделаем подстановку −
x
= t,
тогда![]()
![]() .
.![]()
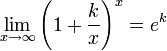
![]()
![]()
![]() для
для
![]() ,
,
![]()
![]()
![]() .
.![]()
![]()
![]() справедливо
равенство
справедливо
равенство
![]()
![]()
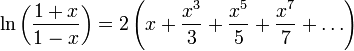





![]()
![]()


![]()


![]() .
.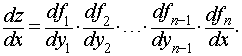
![]()
![]()
![]() где
y0
= f(x0),
и
где
y0
= f(x0),
и
![]() Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы:
![]() Тогда
их композиция также дифференцируема:
Тогда
их композиция также дифференцируема:
![]() и
её производная имеет вид:
и
её производная имеет вид:![]()
![]()
![]() :
:![]()
![]() Тогда
Тогда
![]() ,
и согласно цепному правилу:
,
и согласно цепному правилу:![]()
![]() Тогда
функция
Тогда
функция
![]() может
быть записана в виде композиции
может
быть записана в виде композиции
![]() где
где![]()
![]()
![]()
![]()
![]()
![]() где
y0
= f(x0),
и
где
y0
= f(x0),
и
![]() Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы:
![]() и
и
![]() Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид
Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид![]()
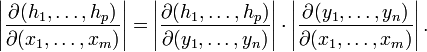

![]() является
обратной к функции
является
обратной к функции
![]() ,
если выполнены следующие тождества:
,
если выполнены следующие тождества:![]()
![]()
![]() является
обратной функцией к x2
на
является
обратной функцией к x2
на
![]() ,
хотя на промежутке
,
хотя на промежутке
![]() обратная
функция другая:
обратная
функция другая:
![]() .
.![]() ,
где a
> 0, то F
− 1(x)
= log ax.
,
где a
> 0, то F
− 1(x)
= log ax.![]() ,
где
,
где
![]() фиксированные
постоянные и
фиксированные
постоянные и
![]() ,
то
,
то
![]()
![]() ,
то
,
то
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() означает
композицию
функций,
а idX,idY —
тождественные
отображения
на X
и Y
соответственно.
означает
композицию
функций,
а idX,idY —
тождественные
отображения
на X
и Y
соответственно.![]() .
.![]() —
биекция. Пусть
—
биекция. Пусть
![]() её
обратная функция. Тогда графики
функций y
= F(x)
и y
= F
− 1(x)
симметричны относительно прямой y
= x.
её
обратная функция. Тогда графики
функций y
= F(x)
и y
= F
− 1(x)
симметричны относительно прямой y
= x.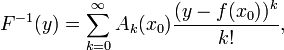


![]() -
дифференцируемая
функция
от аргумента x в некотором интервале
.
Если в уравнении
y
считать аргументом, а x - функцией, то
возникает новая функция
-
дифференцируемая
функция
от аргумента x в некотором интервале
.
Если в уравнении
y
считать аргументом, а x - функцией, то
возникает новая функция
![]() ,
где
,
где
![]() -
функция
обратная данной.
-
функция
обратная данной.![]()
![]() ,
,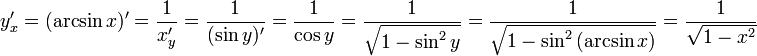
![]() ,
,![]() [1]
[1]
![]() .
.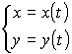
![]() и
в параметрической форм е:
и
в параметрической форм е: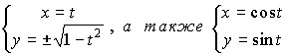
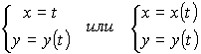
![]()
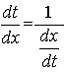
![]() ,
,
![]()
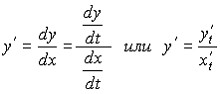
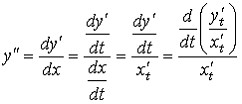
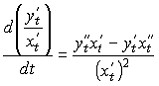
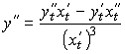
![]()
![]()

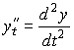
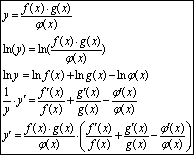
![]()
![]()
![]()
![]() .
. .
.![]()
![]() .
.![]() .
Имеем
.
Имеем![]() ,
,![]() есть постоянная величина, равная 1. Это
очевидно, ибо
- линейная функция и скорость ее изменения
постоянна.
есть постоянная величина, равная 1. Это
очевидно, ибо
- линейная функция и скорость ее изменения
постоянна.![]() ,
то
,
то![]() .
.![]() ,
тогда
,
тогда![]() .
.![]() при
при
![]() .
Докажем, что и вообще производная от
при любом целом положительном показателе
.
Докажем, что и вообще производная от
при любом целом положительном показателе
![]() равна
равна
![]() .
.![]() .
.![]() .
.![]() .
.![]() ,
а остальные стремятся к нулю
вместе с
.
Поэтому
,
а остальные стремятся к нулю
вместе с
.
Поэтому![]() .
.![]() .
.![]() из найденной общей формулы следуют
формулы, выведенные выше.
из найденной общей формулы следуют
формулы, выведенные выше.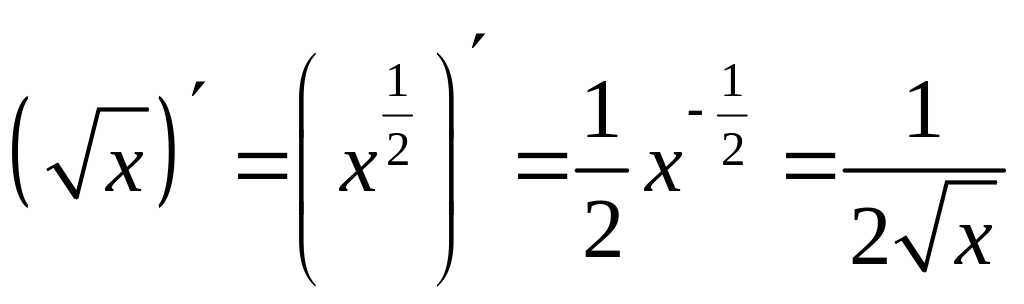 .
.![]() .
.![]() .
Следовательно,
.
Следовательно,![]() ,
,![]() .
.
![]() ,
посмотрим, какой смысл имеет выражение
,
посмотрим, какой смысл имеет выражение
![]() ,
стоящее под знаком этого предела.
,
стоящее под знаком этого предела.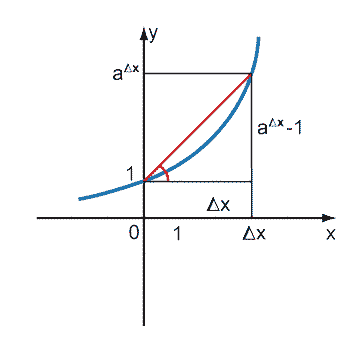
![]() от
нуля. Разность
от
нуля. Разность
![]() окажется
приращением функции в точке 0.
Следовательно, отношение
окажется
тангенсом угла наклона секущей,
проходящей через точку графика с
абсциссой 0.
Но это значит, что
-
это тангенс угла наклона касательной,
проходящей через точку графика с
абсциссой 0.
Мы доказали, что
-
это производная функции
окажется
приращением функции в точке 0.
Следовательно, отношение
окажется
тангенсом угла наклона секущей,
проходящей через точку графика с
абсциссой 0.
Но это значит, что
-
это тангенс угла наклона касательной,
проходящей через точку графика с
абсциссой 0.
Мы доказали, что
-
это производная функции
![]() в
точке 0:
в
точке 0:
![]() ,
,
![]() .
.
![]() пересекает
под углом 45°
ось ординат, а следовательно, и ось
абсцисс. То есть производная функции
в
нуле равна 1.
пересекает
под углом 45°
ось ординат, а следовательно, и ось
абсцисс. То есть производная функции
в
нуле равна 1.
![]() .
.
![]() .
.
![]() .
.
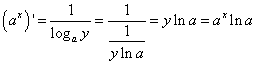 .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
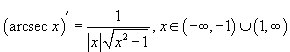
![]()
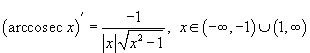
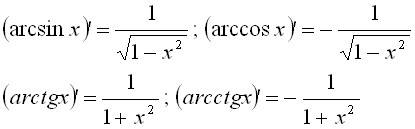
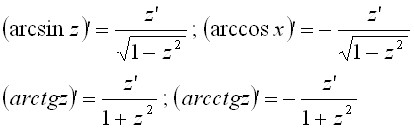
![]() имеет
обратную ф-ию на
имеет
обратную ф-ию на
![]()
![]()
![]()
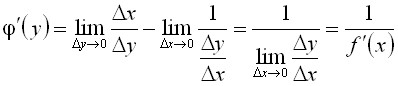
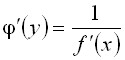
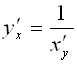
![]()
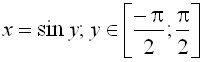
![]()
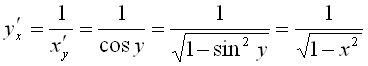
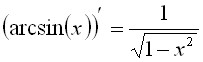
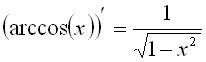

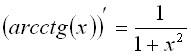
![]() есть
угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
есть
угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
![]() .
.![]() является
угловым коэффициентом секущей, проходящей
через точки M1
(a;
f(a))
и M2(b;
f
(b))
графика функции у
= f(x),
a f
' (c)
— угловой коэффициент касательной к
графику в точке (c;
f (c)).
Из теоремы Лагранжа следует, что
существует точка "c"
такая, что касательная к графику в точке
(c;
f(c))
параллельна секущей M1M2.
Таких точек может быть и несколько, но,
по крайней мере, одна всегда
существует.
Замечание.
Формула Лагранжа по структуре похожа
на формулу линеаризации
является
угловым коэффициентом секущей, проходящей
через точки M1
(a;
f(a))
и M2(b;
f
(b))
графика функции у
= f(x),
a f
' (c)
— угловой коэффициент касательной к
графику в точке (c;
f (c)).
Из теоремы Лагранжа следует, что
существует точка "c"
такая, что касательная к графику в точке
(c;
f(c))
параллельна секущей M1M2.
Таких точек может быть и несколько, но,
по крайней мере, одна всегда
существует.
Замечание.
Формула Лагранжа по структуре похожа
на формулу линеаризации
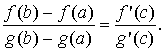
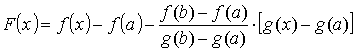 .
.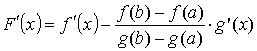 ,
,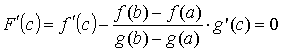 .
.![]() непрерывны
в некоторой окрестности
непрерывны
в некоторой окрестности
![]() точки
точки
![]() и
и
![]() ,
то есть
,
то есть
![]() и
и
![]() при
при
![]() .
Предположим, что при
.
Предположим, что при
![]() функции
и
имеют
производные
функции
и
имеют
производные
![]() и
и
![]() ,
причём существует предел отношения
этих производных:
,
причём существует предел отношения
этих производных:
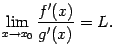
![]() :
:
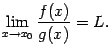
 следует,
что оба односторонних предела также
равны
:
следует,
что оба односторонних предела также
равны
:
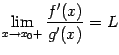 и
и
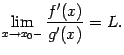
![]() ,
,
![]() .
По теореме Коши, применённой к отрезку
.
По теореме Коши, применённой к отрезку
![]() ,
получим тогда, с учётом того, что
,
получим тогда, с учётом того, что
![]() ,
,
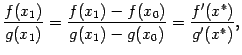
![]() .
Перейдём теперь в этом равенстве к
пределу при
.
Перейдём теперь в этом равенстве к
пределу при
![]() :
:
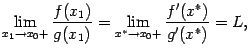
![]() .
Теперь возьмём точку
.
Теперь возьмём точку
![]() ,
,
![]() и
применим теорему Коши к отрезку
и
применим теорему Коши к отрезку
![]() .
Получим
.
Получим

![]() .
Переходя к пределу при
.
Переходя к пределу при
![]() ,
получаем
,
получаем
![]() .
.
![]() равны
.
На основании теоремы о связи односторонних
пределов с двусторонним получаем, что
равны
.
На основании теоремы о связи односторонних
пределов с двусторонним получаем, что
![]() и
и
![]() ):
если
и
бесконечно
малы при
и
существует предел
):
если
и
бесконечно
малы при
и
существует предел
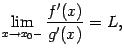
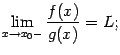
 .
.
![]() и
и
![]() .
.
![]() на
эквивалентную бесконечно малую:
на
эквивалентную бесконечно малую:
![]() при
при
![]() .
Получим:
.
Получим:
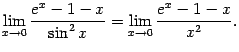
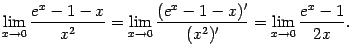
![]() при
.
Получаем:
при
.
Получаем:
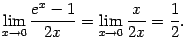
![]() .
По правилу Лопиталя отсюда следует,
что исходный предел также существует
и равен тому же числу:
.
По правилу Лопиталя отсюда следует,
что исходный предел также существует
и равен тому же числу:
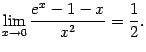
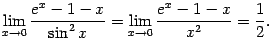
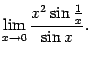 Его
легко вычислить, заметив, что величина
Его
легко вычислить, заметив, что величина
![]() --
величина, локально ограниченная при
базе
,
а величина
--
величина, локально ограниченная при
базе
,
а величина
![]() --
бесконечно малая:
--
бесконечно малая:
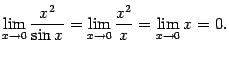
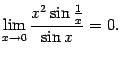
![]() и
и
![]() правило
Лопиталя и вычислить предел отношения
производных этих двух функций. Имеем:
правило
Лопиталя и вычислить предел отношения
производных этих двух функций. Имеем:
![]() и
и
![]() .
Составим отношение этих двух производных:
.
Составим отношение этих двух производных:
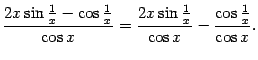
![]() ,
,
![]() ,
,
![]() .
Докажем это.
.
Докажем это.
![]() )
Пусть
и
--
функции, являющиеся бесконечно малыми
при базе
(или
,
или
)
и дифференцируемые на некотором луче
)
Пусть
и
--
функции, являющиеся бесконечно малыми
при базе
(или
,
или
)
и дифференцируемые на некотором луче
![]() (или
(или
![]() ,
или объединении лучей
,
или объединении лучей
![]() ,
соответственно). Тогда если существует
предел
,
соответственно). Тогда если существует
предел
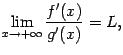
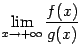 также
существует и равен тому же числу:
также
существует и равен тому же числу:
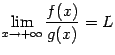
![]() и
рассмотрим функции
и
рассмотрим функции
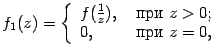 и
и
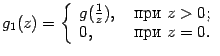 Тогда
функции
Тогда
функции
![]() и
и
![]() непрерывны
на отрезке
непрерывны
на отрезке
![]() и
дифференцируемы при
и
дифференцируемы при
![]() .
При этом
.
При этом
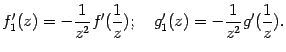
![]() величинам
и
можно
применить правило Лопиталя ( теорема
5.5 для
предела справа, см. замечание
5.5):
величинам
и
можно
применить правило Лопиталя ( теорема
5.5 для
предела справа, см. замечание
5.5):
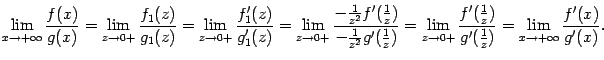
![]() и
и
![]() при
и
в некоторой проколотой окрестности
при
и
в некоторой проколотой окрестности
![]() ,
,
![]() ,
существуют производные
и
.
Тогда, если существует предел отношения
этих производных
,
существуют производные
и
.
Тогда, если существует предел отношения
этих производных
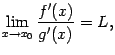
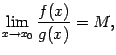
![]() --
некоторое число. Докажем, что тогда
--
некоторое число. Докажем, что тогда
![]() .
.
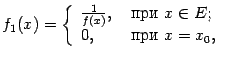 и
и
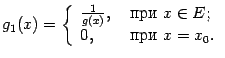
![]() и
и
![]() --
бесконечно малые при
,
непрерывные при
--
бесконечно малые при
,
непрерывные при
![]() ;
их производные таковы:
;
их производные таковы:

![]()
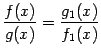
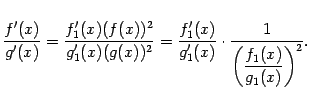
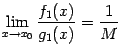 .
Переходя к пределу в равенстве (5.4),
получаем:
.
Переходя к пределу в равенстве (5.4),
получаем:
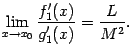
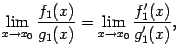
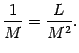
![]() и
и
![]() .
Предел их отношения, очевидно, существует:
.
Предел их отношения, очевидно, существует:
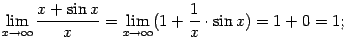
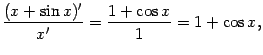
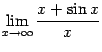
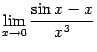 .
(Это предел отношения двух бесконечно
малых. Заметим, что
не
является множителем, так что его нельзя
заменить на эквивалентную величину
.
(Это предел отношения двух бесконечно
малых. Заметим, что
не
является множителем, так что его нельзя
заменить на эквивалентную величину
![]() ;
если бы мы всё же сделали это, то сразу
получили бы в числителе 0, и "ответ"
равнялся бы 0.) Применим правило Лопиталя
и получим, что
;
если бы мы всё же сделали это, то сразу
получили бы в числителе 0, и "ответ"
равнялся бы 0.) Применим правило Лопиталя
и получим, что
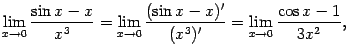
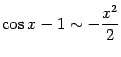 при
,
и заменив числитель. Однако можно пойти
и другим путём. Мы снова получили
отношение двух бесконечно малых, к
которому снова применим правило
Лопиталя:
при
,
и заменив числитель. Однако можно пойти
и другим путём. Мы снова получили
отношение двух бесконечно малых, к
которому снова применим правило
Лопиталя:
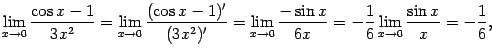
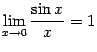 (это
первый замечательный предел).
(это
первый замечательный предел).
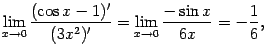
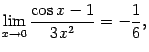
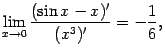
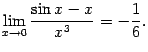

![]() в
самой точке xо.
Если f
(xо)
= 0,
>0
(
<0),
то точка xо
является
точкой локального минимума (максимума)
функции f(x).
Если же
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
в
самой точке xо.
Если f
(xо)
= 0,
>0
(
<0),
то точка xо
является
точкой локального минимума (максимума)
функции f(x).
Если же
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.![]() (a,b),
причем точка (x0,
f(x0))
является критической точкой графика
функции f.
Тогда, если при переходе через x0
производная меняет знак с плюса на
минус (с минуса на плюс), то f'(x0)
– максимум (минимум) функции f.
(a,b),
причем точка (x0,
f(x0))
является критической точкой графика
функции f.
Тогда, если при переходе через x0
производная меняет знак с плюса на
минус (с минуса на плюс), то f'(x0)
– максимум (минимум) функции f.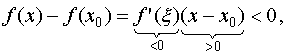
![]() ,
если Δx <
0, то
,
если Δx <
0, то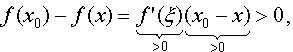
![]()