Свойства непрерывных функций

1. Если ф-ция y=f(x) непрерывна на [a,b] и f(a)*f(b)<0, т.е. знаки f(a) и f(b) противоположны, то на (a,b)  найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.

2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.

3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).

в точке:

1. если ф-ция f(x) и g(x) непрерывна в х0, то их сумма, произведение, частное (при φ(х0)≠0) явл. ф-циями, непрерывными в х0

2. если ф-ция y=f(x) непрерывна в х0, и f(x0)>0, то существует окрестность х0, в которой f(x)>0

3. если y=f(U) непрерывна в U0, а U=φ(x) непрерывна в U0=φ(x0), то сложная ф-ция y=f[φ(x)] непрерывна в х0.

Свойства непрерывных функций. Непрерывность сложной функции

Теорема 1. Пусть функции f(x) и g(x) непрерывны в точке х₀. Тогда функция f(x) не равная g(x), f(x)g(x) и (если g(x) не равно 0) непрерывны в точке x0.

Доказательство.

Пусть f(x) и g(x) непрерывны в точке x₀. Это значит, что . Но тогда, по свойствам пределов

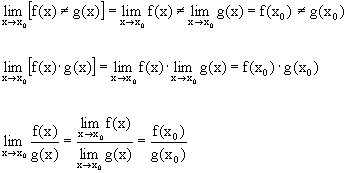
Последнее свойство верно, если . 

Пусть y=f(x), но x, в свою очередь, является функцией некоторого аргумента t: x=(t). Тогда комбинация y=f((t)) называется сложной функцией, или суперпозицией функции (t).

Примеры:

а) y=sin(x), x=e^t => y=sin(e^t)

б) y= e^x , x=sin(t) => y= e^sin(t)

 

Теорема о непрерывности сложной функции.

Пусть функция (t) непрерывна в точке t₀ и функция f(x) непрерывна в точке х₀=(t₀). Тогда функция f((t)) непрерывна в точке t₀.

Доказательство.

Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

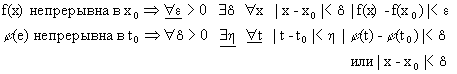
Выписывая подчеркнутые кванторы, получим, что

,

что и говорит о том, что f((t)) непрерывна в точке t₀. 

Обратите внимание на следующие детали:

а) т.к. x=(t), то |(t)-(t₀)|< может быть записано как |x-x₀|<, и f(x) превращается в F((t));

б) при определении непрерывности (t) в точке t₀ в первом кванторе стоит буква . Это необходимо для согласования с квантором в предыдущей строке и взаимного уничтожения . Любая другая буква на этом месте не дала бы верного результата.

Теоремы о непрерывных функциях

Перейдем к доказательству важнейших теорем о непрерывных функциях.

Первая теорема Больцано-Коши.Пусть f(x) определена и непрерывна на отрезке [a,b] и на концах этого отрезка принимает разные по знаку значения.Тогда существует такая точка с принадлежащая [а,b] в которой f(c)=0.

Доказательство.

Пусть, для определенности, f(a)<0, f(b)>0. Ситуация выглядит так:

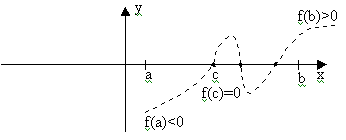
Для доказательства теоремы снова используем метод деления отрезка пополам.

1. Деление отрезков пополам.

Разделим отрезок [a, b] пополам. Середина его будет точка . Тогда возможны такие варианты:

а) . В этом случае, взяв , теорему можно считать доказанной.

б) . В этом случае для дальнейшего рассмотрения оставим отрезок , который обозначим [a₁, b₁].

в) В этом случае для дальнейшего рассмотрения оставим отрезок , который обозначим [a₁, b₁].

Проделаем такую же процедуру с отрезком [a₁, b₁], получив отрезок [a₂, b₂], затем то же самое с отрезком [a₂, b₂], получив отрезок [a₃, b₃] и т.д. Заметим, что для дальнейшего рассмотрения все время оставляется тот отрезок, для которого f(a_n)<0 и f(b_n)>0.

2. Построение точки С.

В результате этой процедуры возможны два варианта.

А. На каком-то шаге n получится, что . В этом случае в качестве точки С следует взять и теорема будет доказана.

Б. .

В этом случае мы получаем систему отрезков [a_n, b_n], для которой

а) [a,b][a₁, b₁] [a₂, b₂][a₃, b₃]…

б)

в)f(a_n)<0; f(b_n)>0

Но тогда, по лемме о вложенных отрезках, существует . Используя непрерывность функции f(x), получим

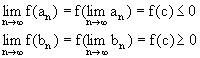
т.к. всегда было f(a_n)<0, f(b_n)>0. Сравнивая эти два неравенства получим, что f(c)=0, что и требовалось доказать.

Вторая теорема Больцано-Коши. Пустьf(x) определена и непрерывна на отрезке <a,b> и . Тогда m<C<M с<a,b> f(c)=C.

Примечание. Символ < означает любой из двух символов – ( или [, а символ > - любой из двух символов - ) или ]. Таким образом, отрезок <a, b> означает любой из следующих отрезков – [a,b], (a,b], [a,b), или (a,b).

Доказательство.

Так как к супремуму и инфимуму можно подойти сколь угодно близко, то можно утверждать, что

x₁<a, b> m<f(x₁)<C

x₂<a, b> C<f(x₂)<M

Очевидно, что отрезок [x₁, x₂] <a, b>.

Рассмотрим функцию  (x)=f(x)-C. Для нее имеем:

 (x₁)=f(x₁)-C<0;  (x₂)=f(x₂)-C>0.

Согласно первой теореме Больцано-Коши, с<a, b>, такая, что  (с)=0. Но тогда эта же точка с<a, b> и для нее (с)=f(c)-C=0, т.е. f(c)=C. 

Первая теорема Вейерштрасса.

Пусть функция f(x) определена и непрерывна на замкнутом отрезке [a, b]. Тогда она ограничена на этом отрезке, т.е. существуют такие числа m и M, что x принадлежащего [a,b] f(x) больше либо равно m и меньше либо равно M.

Доказательство.

Доказательство этой теоремы проведем методом от противного.

Предположим противное – пусть, например, функция f(x) неограничена сверху.

1. Построение последовательности. Мы предположили, что f(x) неограничена сверху на [a,b]. Это означает, что для любого числа А найдется такая точка x[a,b], что f(x)>A.

Возьмем в качестве числа А числа 1, 2, 3, 4,… Тогда , что f(x_n)>n.Мы получили, таким образом, некоторую последовательность {x_n}[a,b] и удовлетворяющую свойству f(x_n)>n.

2. Выделение подпоследовательности. Так как последовательность {x_n} ограничена, то по лемме Больцано-Вейерштрасса из нее можно выделить сходящуюся последовательность {x_n}, т.е. 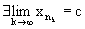. В силу замкнутостиотрезка [a, b] точка c [a,b]. (Отметим,что в этом месте используется ограничение теоремы – замкнутость [a,b]. Если бы, например, был (a,b), то с могла бы и не принадлежать (a,b)).

3. Сведение к противоречию.Т.к. согласно п.1 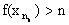, то, переходя к пределу kполучим 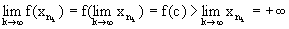т.е. f(c)=+, что противоречит условию теоремы, где сказано, что f(x) определена на отрезке [a,b],что означает, что f(c) должна иметь конечное значение. 

Вторая теорема Вейерштрасса.

Пусть функция f(x) определена и непрерывна на замкнутом отрезке[a,b]. Тогда существуют такие точки x₁, x₂ принадлежащие [a,b], что , т.е. инфимум и супремум f(x) достигаются на [a,b].

Доказательство.

Докажем теорему только для супремума.

1. Построение последовательности. По первой теореме Вейерштрасса, f(x) ограничена сверху на [a,b],т.е.

По свойствам супремума, к нему можно подойти сколь угодно близко. Поэтому . Беря n=1,2,3,… получим последовательность {x₁, x₂, x₃,…}такую, что .

2. Выделение подпоследовательности. Т.к. n a x_n b, то по лемме Больцано-Вейерштрасса, из последовательности {x_n} можно выделить сходящуюся подпоследовательность 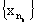такую, что , причем с[a,b] в силу его замкнутости.

3. Достижение супремума. Для нашей подпоследовательности верно условие

.

4.Переходя к пределу k получим

.

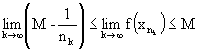Но , кроме того, в силу непрерывности f(x), . В результате получим, что Mf(c) M, т.е. f(c)=M и супремум f(x) достигается в точке с.