Второй замечательный предел

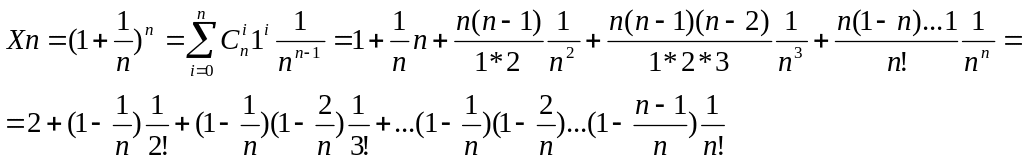
X n Xn3

Предел функции непрерывного аргумента

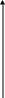
y=f(x) X

a,b

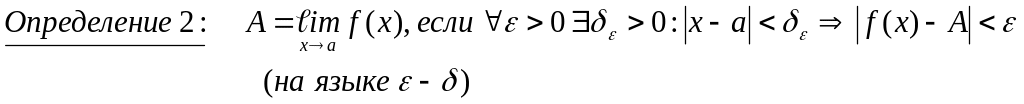
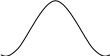
Первый замечательный предел

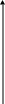
В торая форма второго замечательного предела

Третий замечательный предел

Т ретья форма второго замечательного предела

П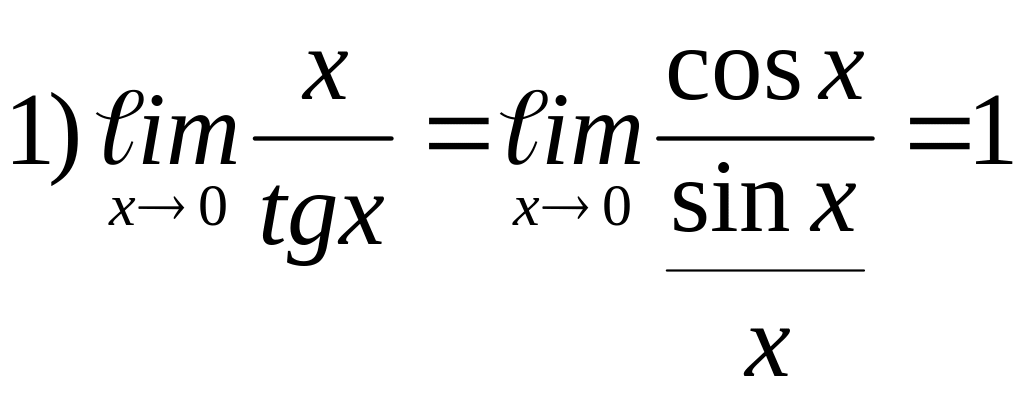 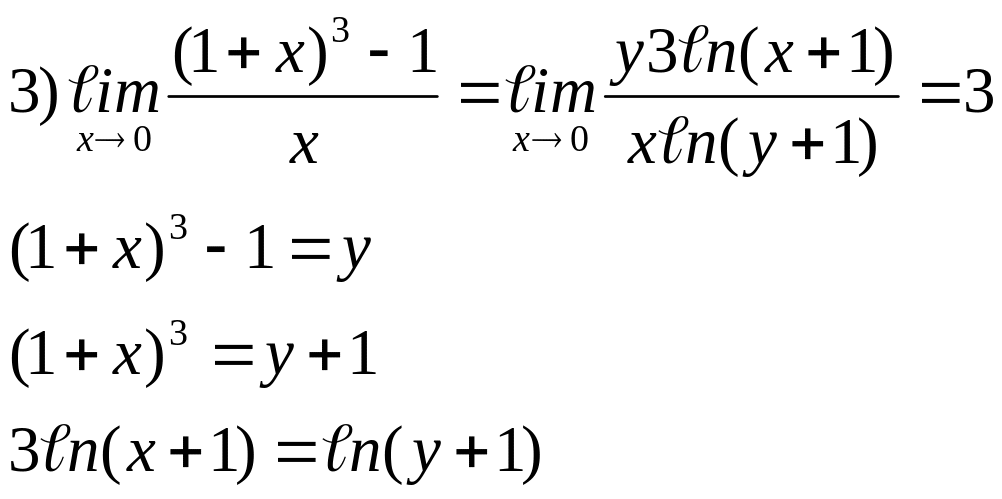римеры:

Теоремы о пределах.

Лемма о вложенных промежутках.

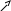
Xn

XnYn n

Y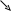 n

Yn-Xn0 -бесконечно малая величина 

Доказательство:

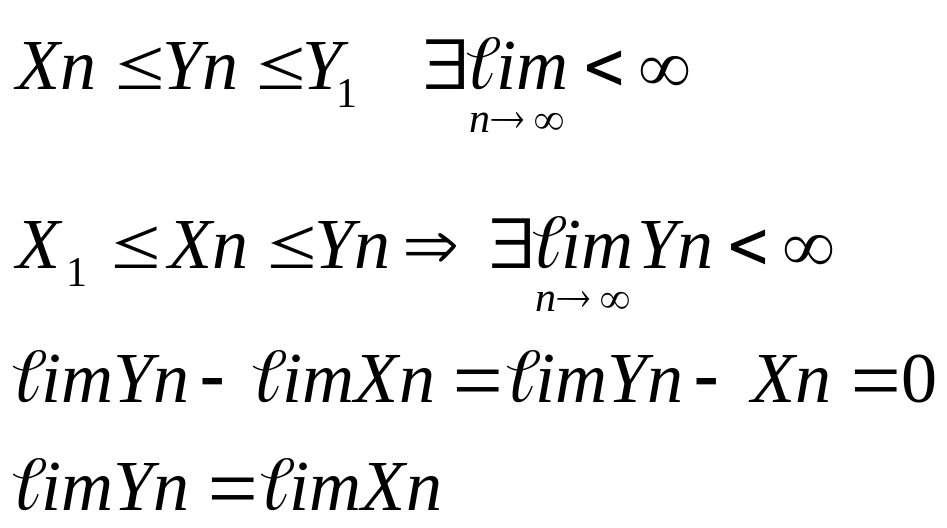
Лемма Больцано-Вейштрасса

Д ля всякой ограниченной поверхности можно выделить сходящую последовательность

Xn₁ Xn₂ Xn_k

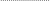
a- нижняя граница;b- верхняя граница

н а к^м шаге мы имеем a^k и b^k.

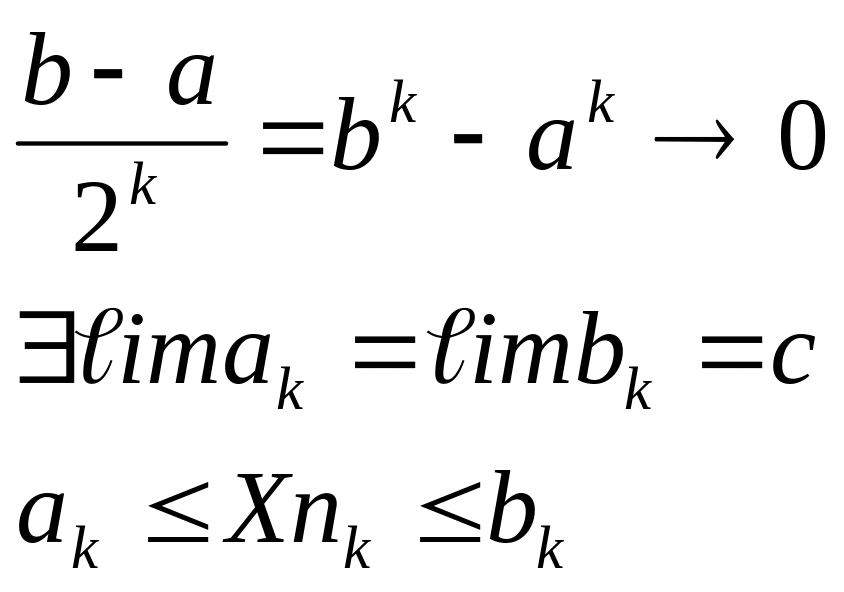
Критерии Коши

(необходимое и достаточное условие сходимости)

Из условия Коши вытекает условие сходимости.

Условие Коши (А)

Определение сходимости (В)

BA

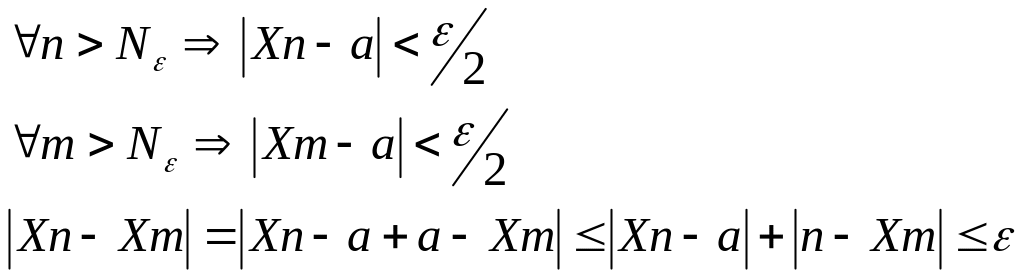
AB

Р аздвинем границы так чтобы Xn M

m =n_k

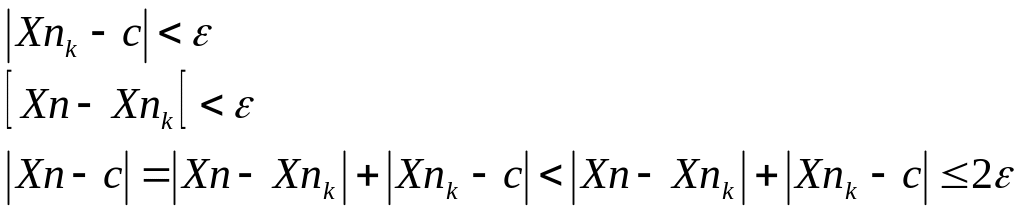
Непрерывность

( )

П риращение аргумента

П риращение функции

н епрерывна в точке Х₀

Этапы проверки непрерывности:

Классификация точек разрыва

Если в некоторой точке Х₀ выполняются первые 2 условия непрерывности (4), но не выполняется какое-то из последних двух, то точка Х₀ называется точкой разрыва 1-го рода (точка устранимого разрыва).

Если же в точке Х₀ не выполняется какое-то из первых двух условий, то она называется точкой разрыва 2-го рода (точкой неустранимого разрыва).

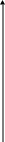
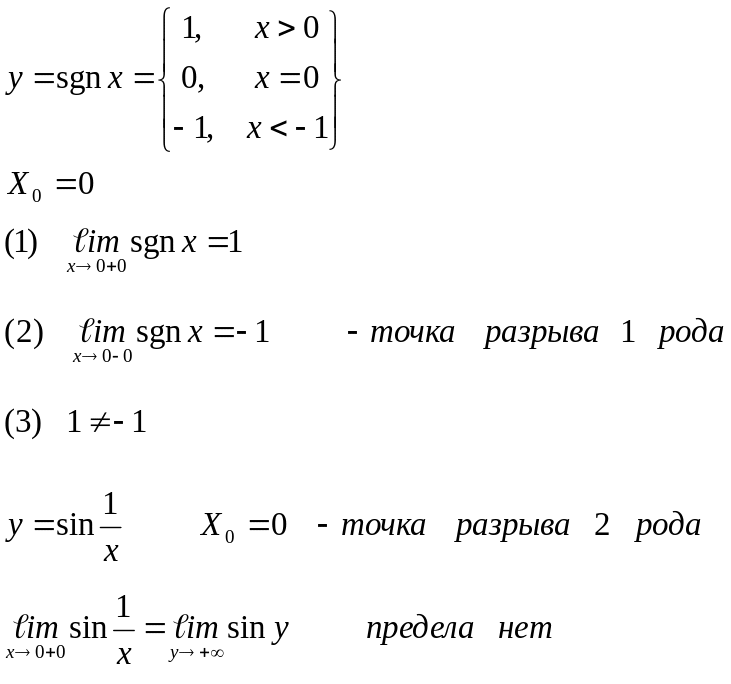
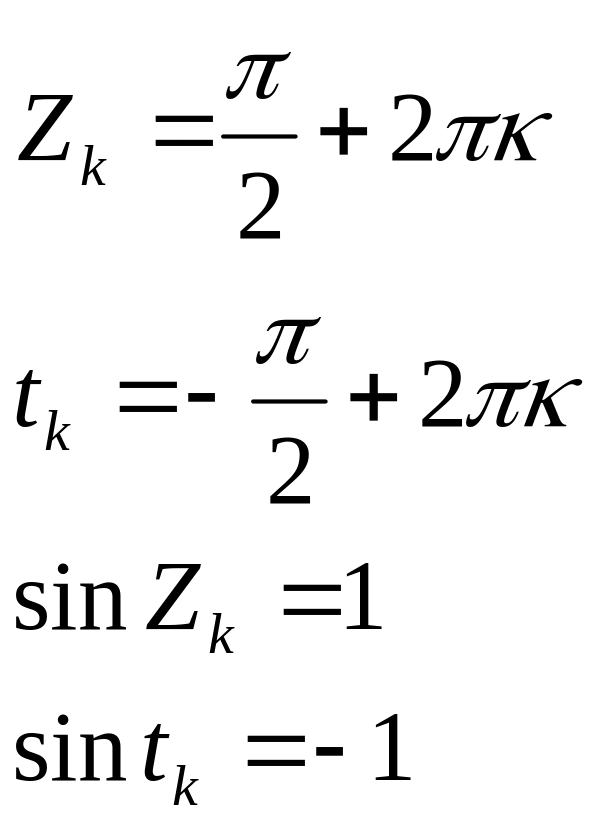
Первая теорема Больцано-Коши

Пусть функция f(x) непрерывна на отрезке ab и на концах отрезка принимает значения разных знаков.

Тогда находится такая точка С из интервала (a,b), что f(C)=0

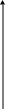
Доказательство:

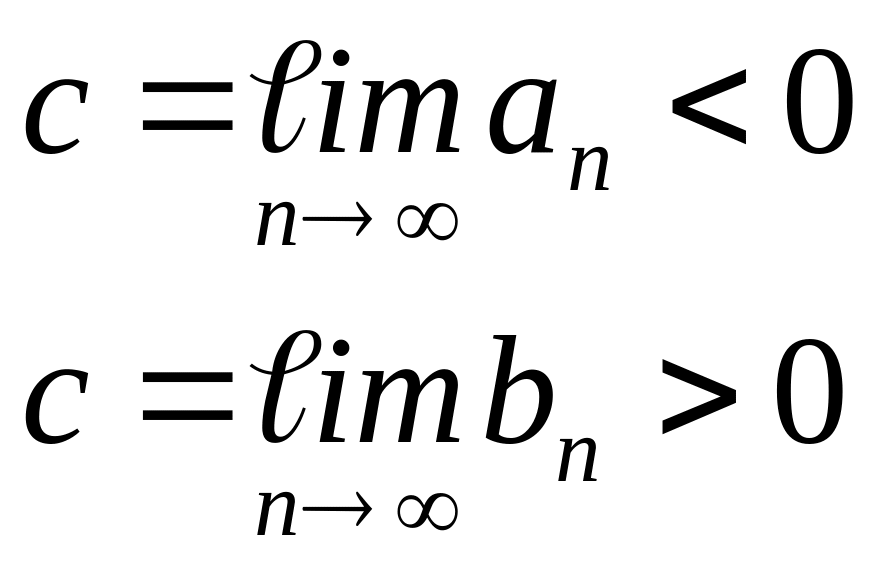
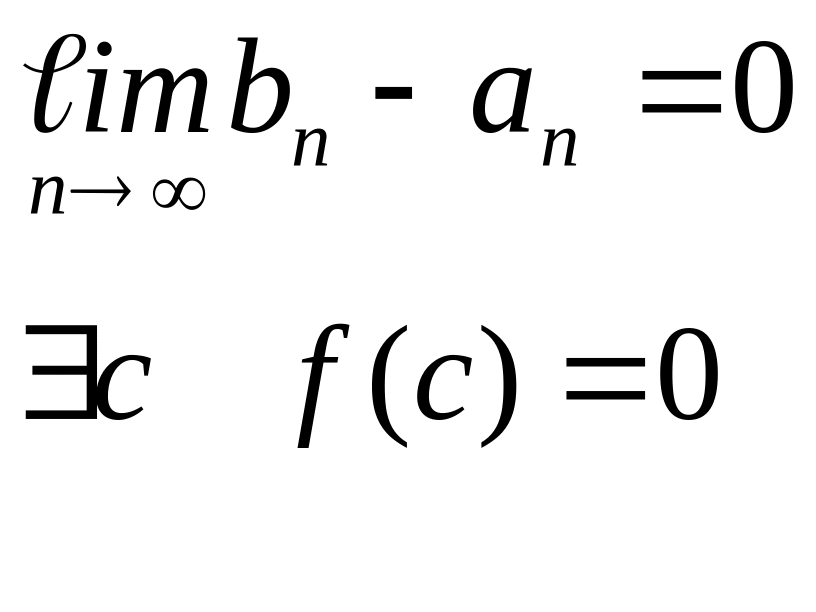
Вторая теорема Больцано-Коши

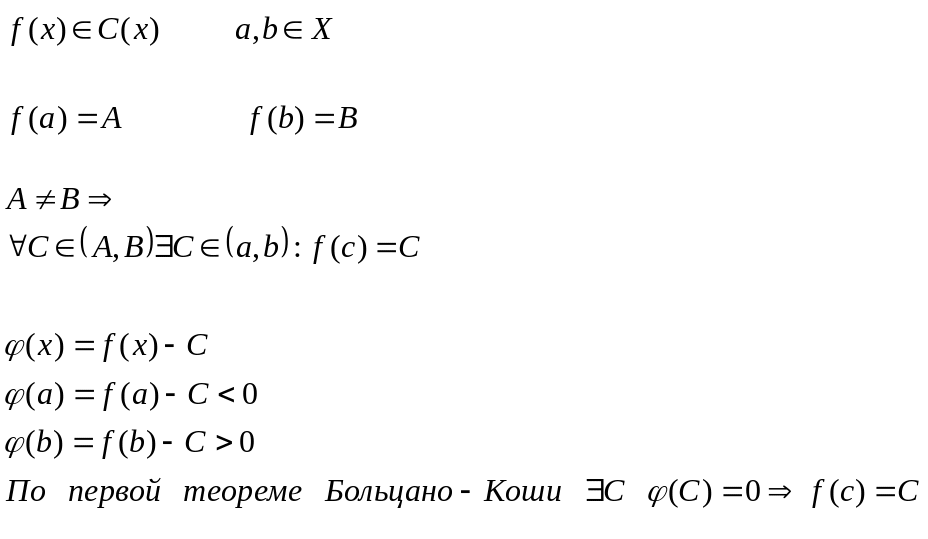
Первая теорема Вейерштрасса

Функция непрерывная на замкнутом промежутке ограничена

Д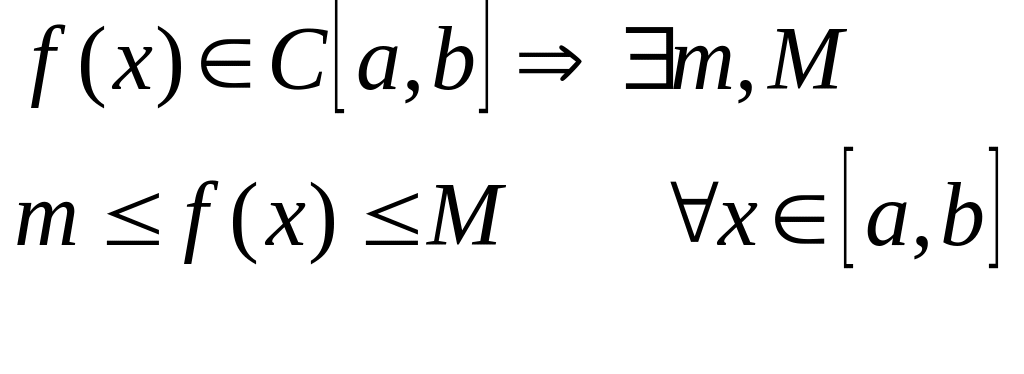 оказательство: (от противного)

F(x) неограничена  n  такое Xna,bf(Xn)n

По лемме Больцано-Вейерштрасса  Xn_kX₀

Вторая теорема Вейерштрасса

Если функция f(x)- непрерывна на отрезке a,b, то она достигает на этом отрезке своей точкой верхней и нижней границы.

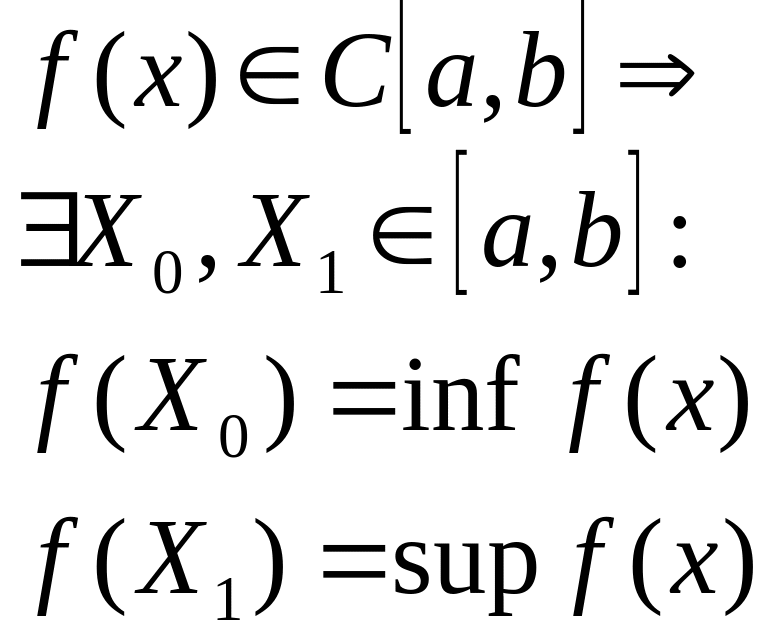
Доказательство:

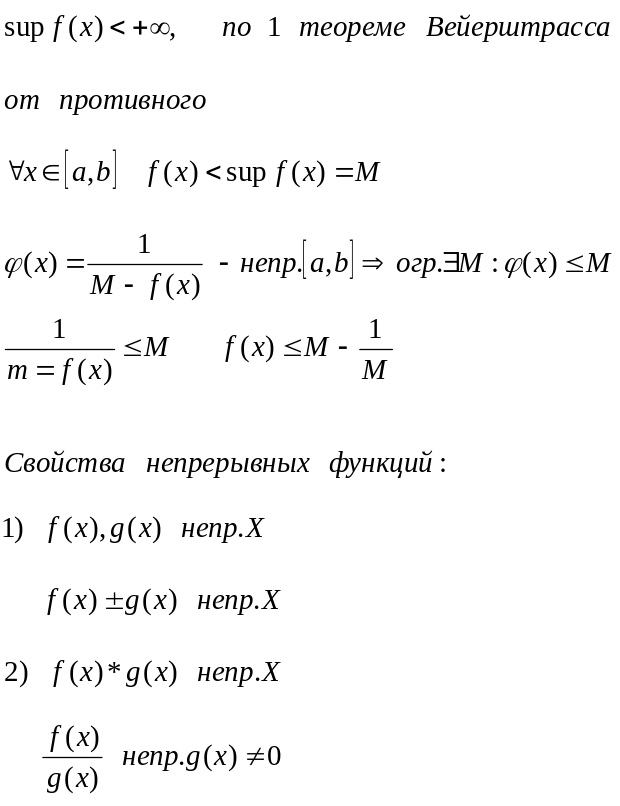
Производная

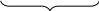
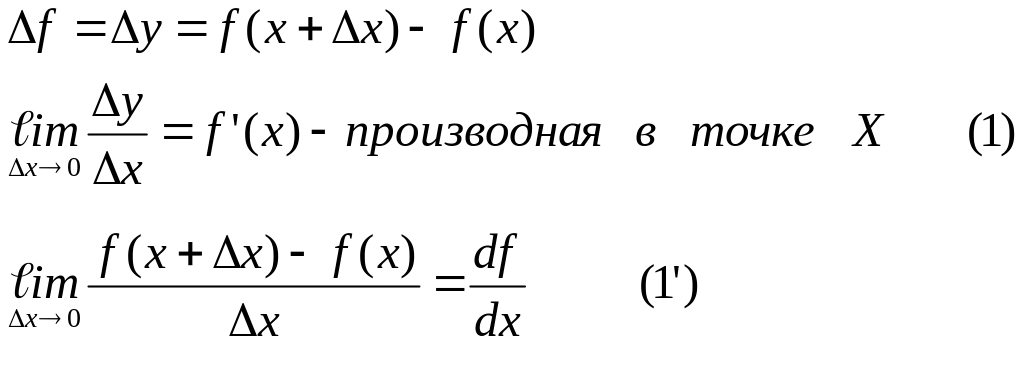
Производной функции в точке называется предел отношений приращения функции к приращению аргумента.

Геометрический смысл:

Геометрическая производная равна тангенсу угла наклона касательной к графику функции в точке Х.

Производная выражает скорость изменения функции.

Пример:

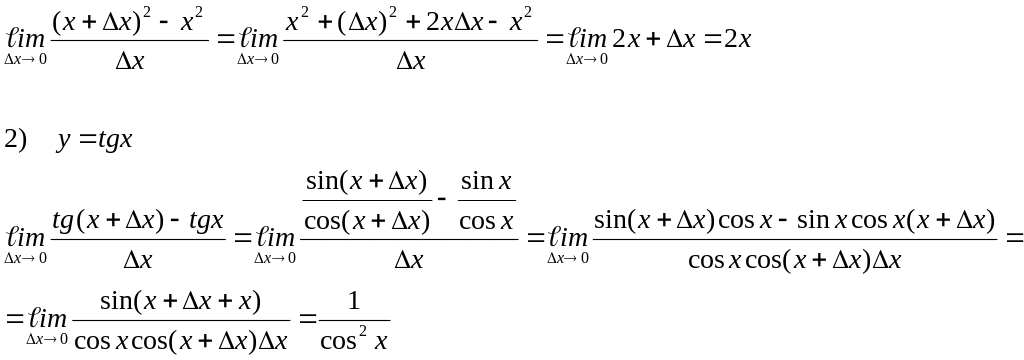
Теорема

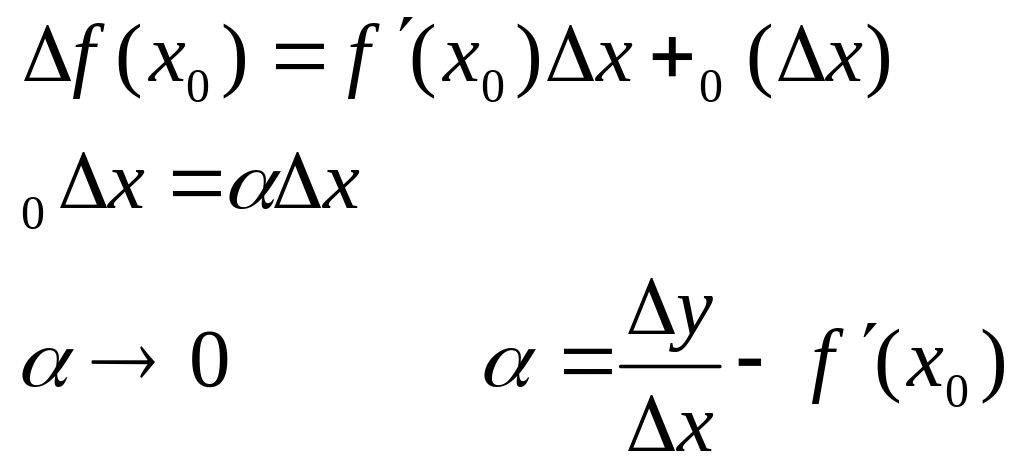
Теорема о производных сложной функции

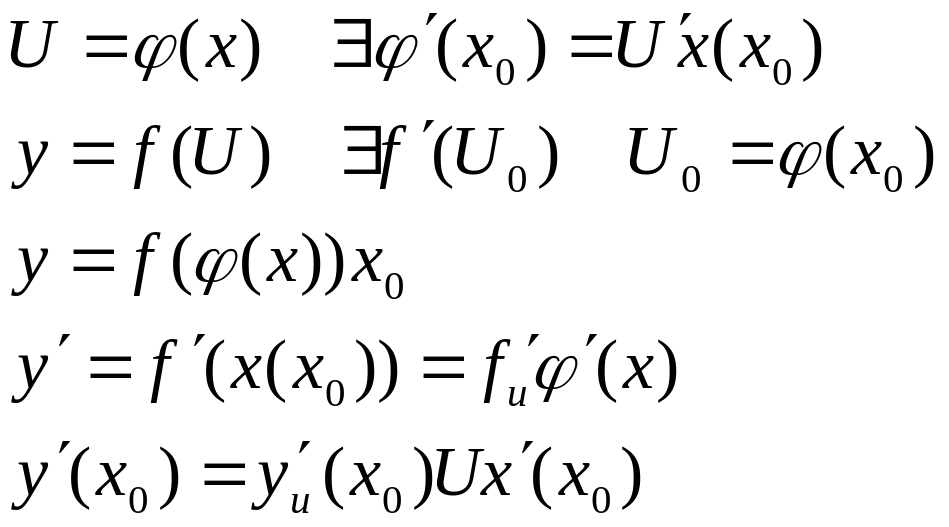
Доказательство:

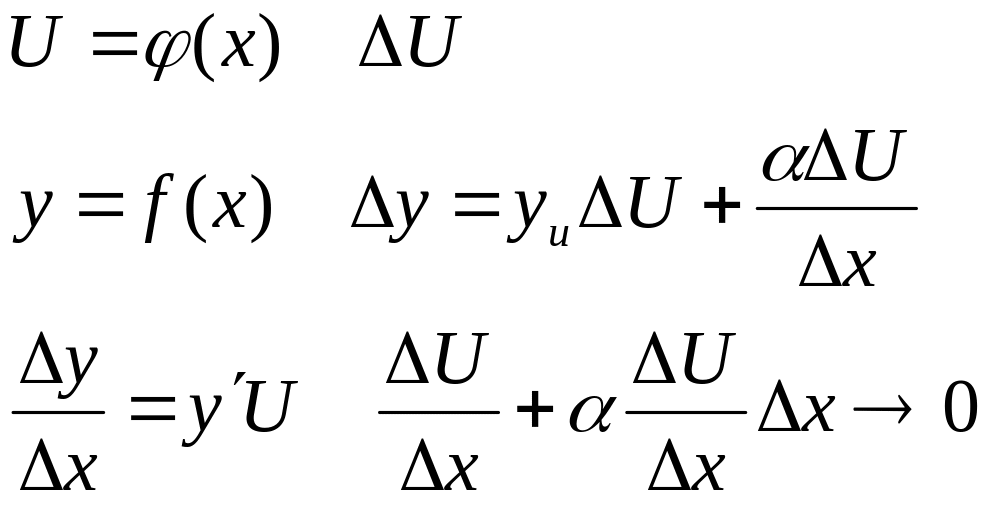
Теорема о производной обратной функции

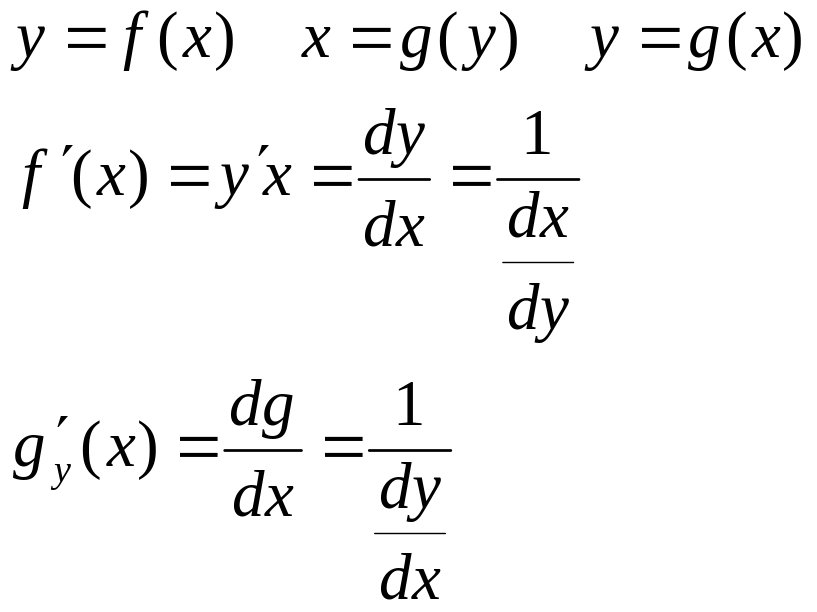
Чтобы найти производную обратной функции достаточно найти обратную величину производной прямой функции и подставить туда значение y=y_x

Дифференциал

Г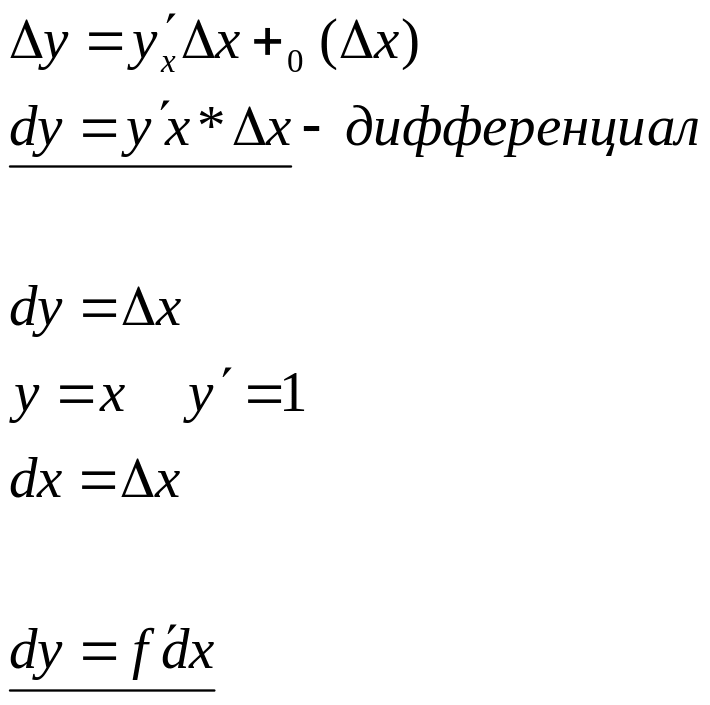 еометрический дифференциал функции в точке Х на промежутке Х есть приращение ординаты касательной на этом промежутке.

Производная высших порядков

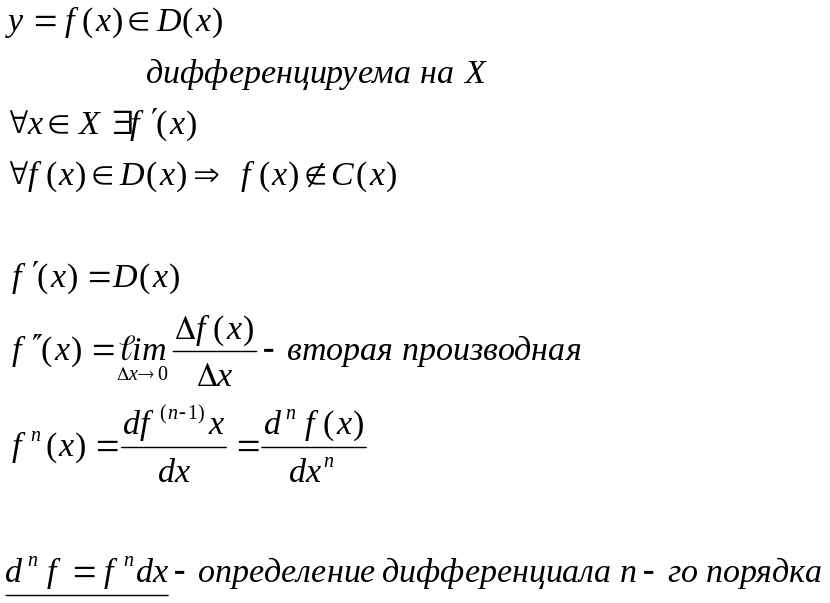
Формула Тейлора

Производная параметрически заданная и неявная

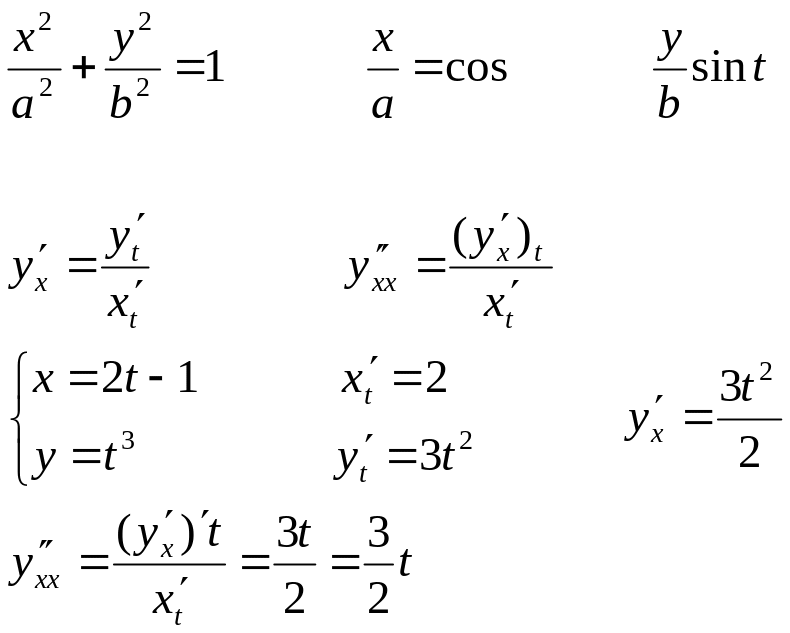
Чтобы найти производную неявной заданной функции нужно продифференцировать и левую и правую часть от f(x,y)=0, считая, что y=y(x) и из полученного уравнения выразить y.

Теоремы о дифференцируемых функциях

Теорема Ролля

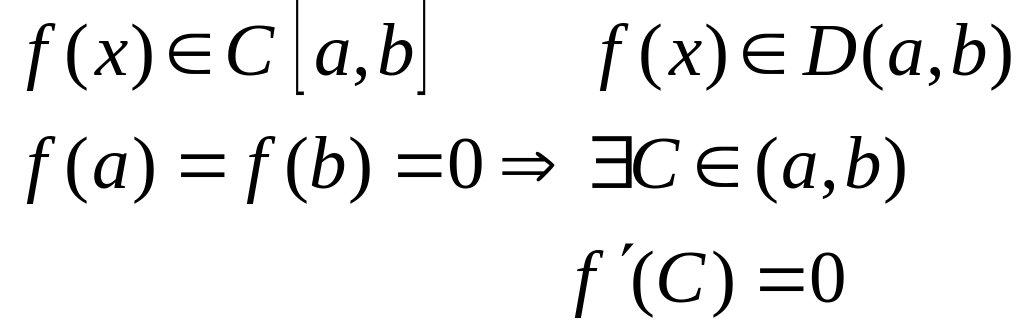
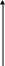Y

X

a b

Доказательство по теореме Вейерштрасса:

Теорема Лагранжа

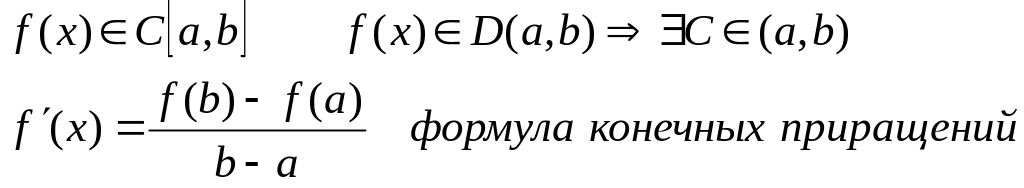
Доказательство:

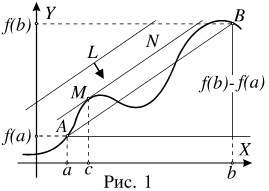
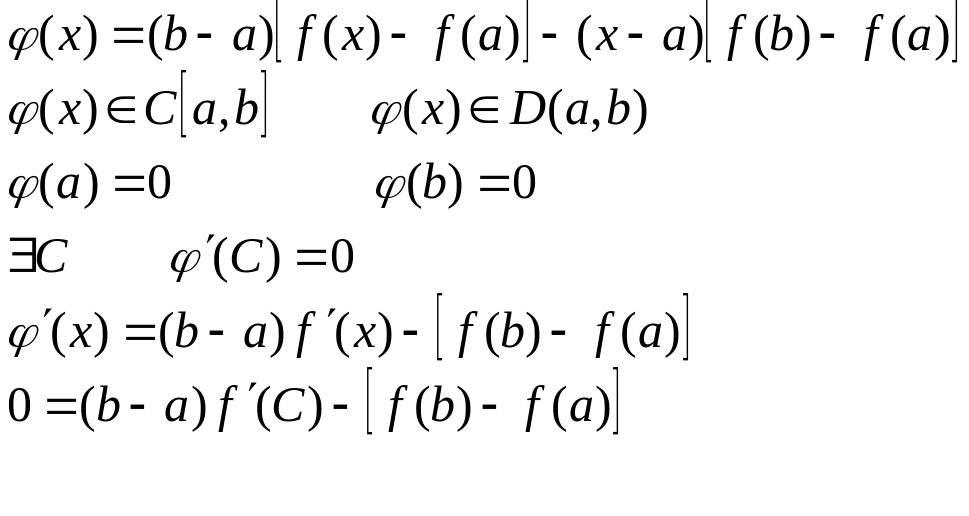
Т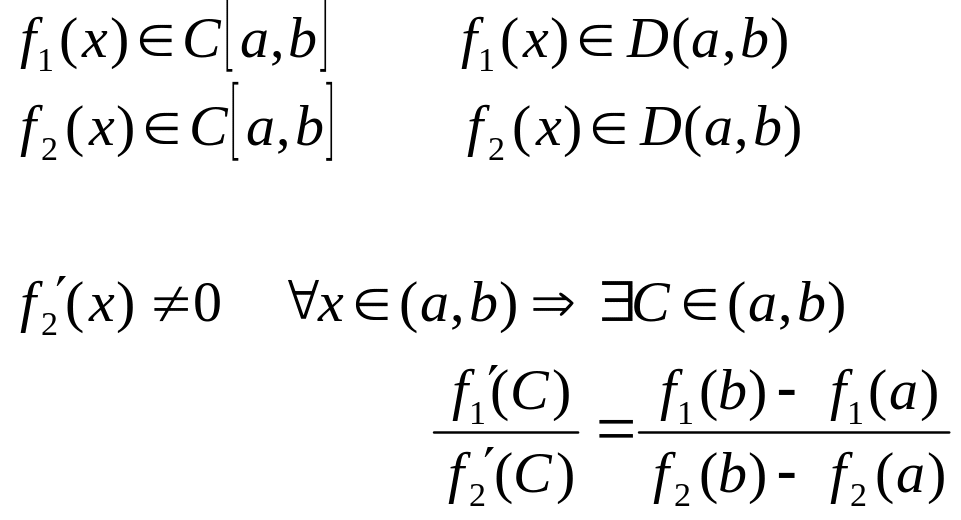 еорема Коши

Доказательство:

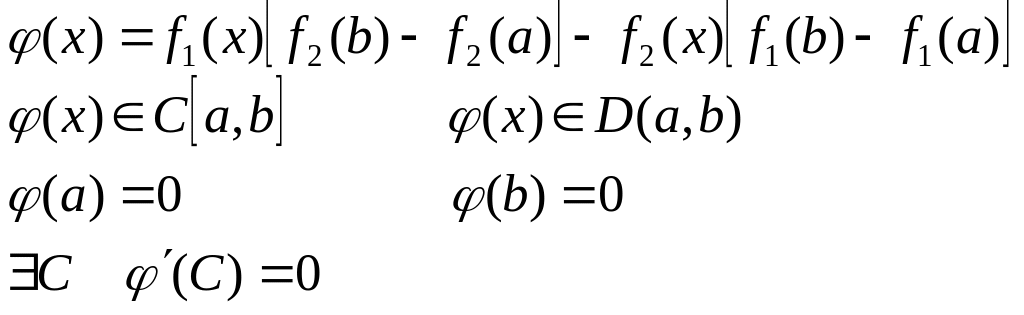
Правило Лопиталя

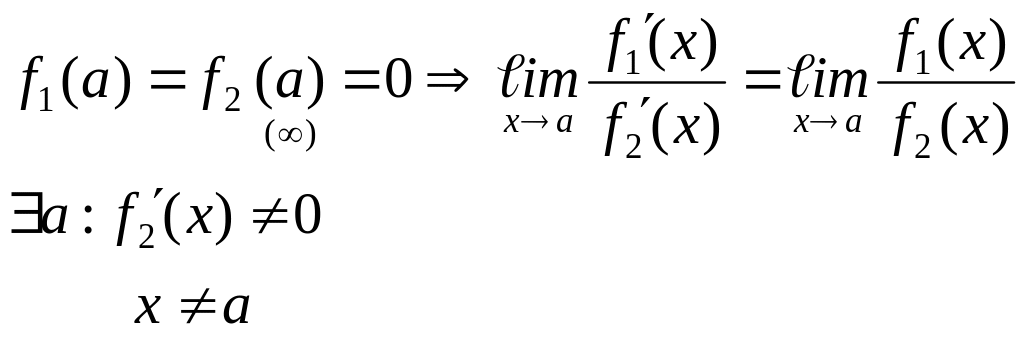
Доказательство формулы Тейлора

Общая схема исследования функций

1. Элементарное

1. Область определения

2. Симметричность и периодичность

а) четность f(-x)=f(x)

б) нечетность f(-x)=-f(x)

в) не четная; не нечетная

г) периодичность  Т0:f(x+T)=f(x)x

Если функция является суперпозицией непериодических, то она непериодическая.

3. Предельные значения

4. Асимптоты

y=kx+b называется асимптотой, если расстояние между графиком функции и графиком асимптоты стремится к нулю.

а ) вертикальная

б) горизонтальная

в ) наклонная

5. Точки пересечения с осями координат

6. Непрерывность и типы разрывов

7. Эскиз графика

2. Исследование по первой производной

1. Найти решения уравнений

2. Точки, подозрительные на экстремум, типы экстремума

3. Значение функции в точках экстремума

4. Интервалы монотонности

5. Уточнить эскиз

3. Исследование по старшим производным

1) Решения уравнений

2 ) Точки, подозрительные на период.числ. с помощью достаточного условия

1. Значения функции в точках перегиба

2. Интервалы выпуклости и вогнутости

3. Окончательный график (в масштабе)

Локальные экстремумы функции

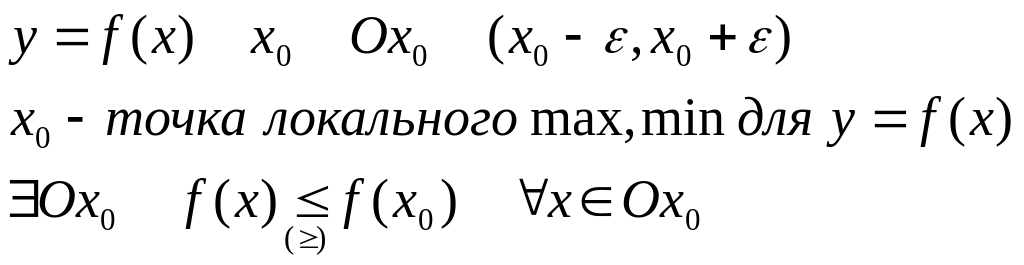
Теорема Ферма(необходимое условие экстремума)

Доказательство:

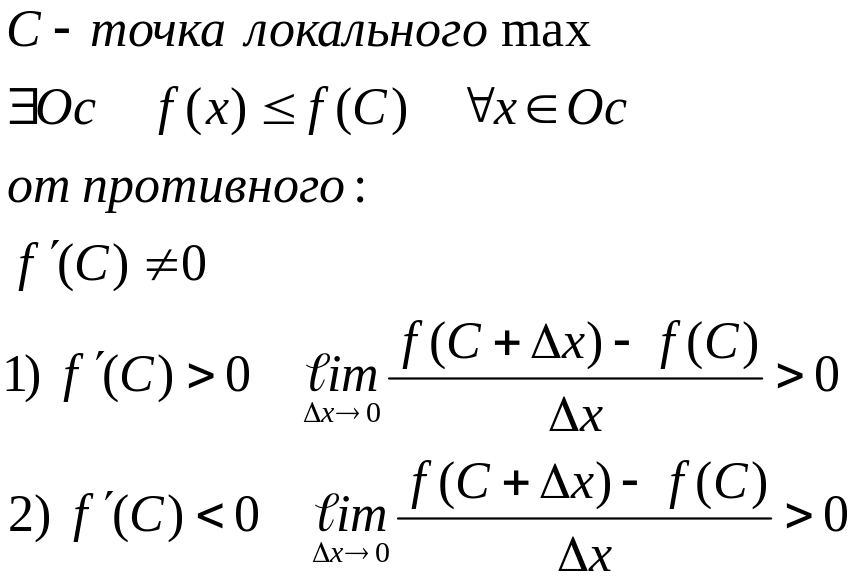
У словие монотонности функции на промежутке

Достаточные условия экстремума

Выпуклость (вогнутость) функции и точки перегиба

y=f(x)

a=x₁ b=x₂ Х

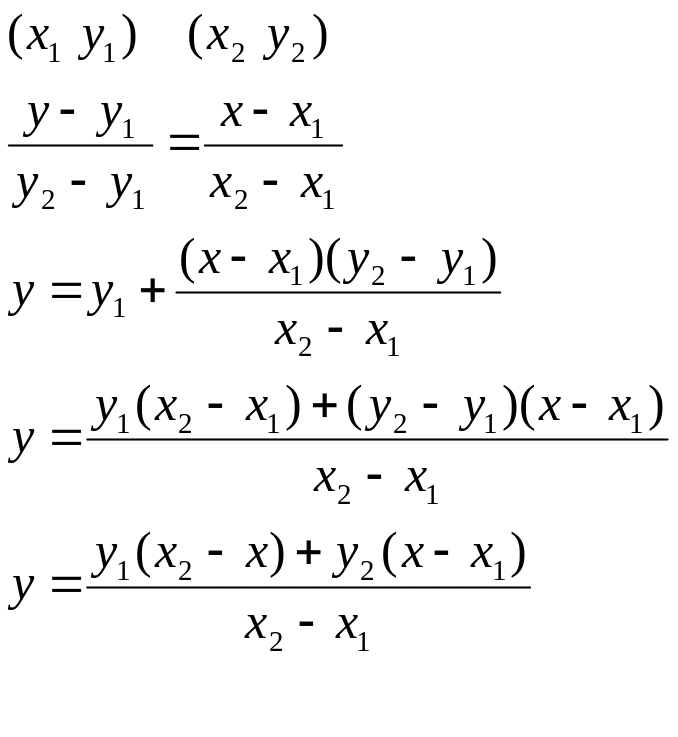
Функция y=f(x) называется выпуклой вверх (выпукла) на интервале (a,b), если для любых точек х₁,х₂ из интервала (a,b), причем выполняется соотношение ах₁х₂b и для любой точки х₀ выполняется неравенство l(x₀)f(x₀)

Функция y=f(x) выпукла вниз (вогнута) на (a,b)  х₁,х₂  (a,b) a<x₁<x₂<b  x₀  (a,b)

L(x₀)f(x₀)

y=x²