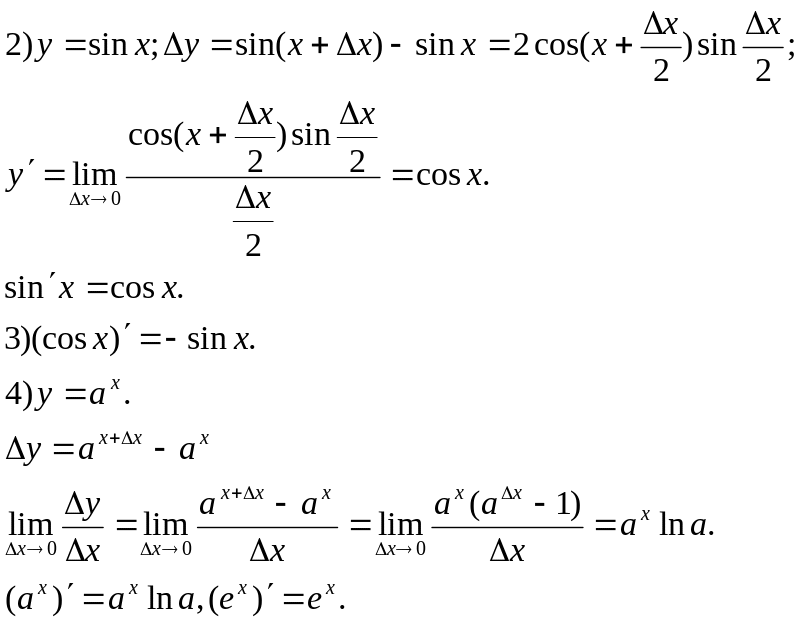§27. Графич. Изоб-е ф-ции.

1. График ф-ции.

В § 7 мы дали опр-е графика ф-ции. Пусть задана ф-ция f(x) на Е, тогда графиком f(x) наз. всё мн-во упорядоч. пар (x,f(x)), где . Для постр-я графика ф-ции y=f(x) необходимо нанести на корд-ю пл-ть ХОУ мн-во точек с координатами (x_i ;f(x_i)), являющихся характерными точками для заданной ф-ции, а затем соединить эти точки линией, учитывая хар-р (св-ва) данной ф-ции.

2. Асимптоты кривой.

Опр.: асимптотой наз. прямая, расстояние от которой до графика ф-ции стремится к нулю, когда точка М(x; f(x)) оставаясь на графике уходит в бесконечность при , либо .

Асимптоты бывают вертикальные или наклонные, в частности, горизонтальные.

Прямая х=а наз. вертикальной асимптотой графика ф-ции f(x), если хотя бы один из пределов или равен бесконечности опред. знака.

Прямая y=kx+в наз. наклонной асимптотой графика ф-ции y=f(x) при , если эта ф-ция f(x)может быть представлена в виде - б.м.ф. при х .

Для того чтобы график ф-ции y=f(x) при либо имеем наклонную асимптоту y=kx+в необх. и дост., чтоб существовали 2 предельных значения: эта теорема очевидна, из опр. наклонной асимптоты. При к=0 из накл. асимптоты получаем y=в – горез. асимптоту, т.е. у=в явл. гориз. асимптотой, если .

Если ф-ция f(x) представима в виде - б.м.ф. при , то говорят, что ф-ции f(x) и g(x) наз. асимптотически равными при .

3. Выпуклые ф-ции.

Пусть задана y=f(x) на инт-ле (а;в). Говорят, что ф-ция y=f(x) имеет график выпуклым внизу (вогнутым), если для выбор. х₁ и х₂ и любого фиксир. , удовлю условию будет выполнятся нер-во . И будет наз. выпуклой вверх, если при тех же условиях будет выполняться нер-во. . Выпуклотость вверх часто наз. просто выпуклотостью.

4. Построение графиков.

Для того, чтобы более точно построить график ф-ции, нужно исслед-ть её. Схема иссл-я ф-ции может быть произвольной.

Дифференциальное исчисление функций одной переменной.

§1. Понятие производной ф-ции.

В §22 части I мы ввели понятие приращения аргумента и преращения ф-ции (см. опр. 5).

Пусть дана ф-ция y=f(x) в некот. окр. точки . Пусть , тогда

.

Определение 1. Если существует конечный предел отношения преращения ф-ции к приращению аргумента при стремлении последнего к нулю: , то этот предел наз. производной ф-ции f в точке х₀ и обозначается f^/ (x₀), . Таким образом илчи (знак ∞ существенен), тоговорят, что ф-ция f(x) в токе х₀ имеет бесконечную производную = +∞ или -∞ соответственно.

Если ф-ция имеет производную в точке х₀, то в этом случае будем считать только существование крнечного предела, т.е. конечной производной.

Опр. 2: если ф-ция f определена в некотор. правосторонней (левост.) окр-ти точки х₀ и конечный или бесконеч. опр. знака предел , то этот предел наз. соответственно конечной или бесконечной правой (левой) производной ф-ции f в точке х₀ и обозначают соответственно: .

Правая и левая произв. наз. односторонними.

Из т. 2 §16 об одностор. пределах следует, что ф-ции f(x), заданная в окр. х₀ имеет производную тогда и только тогда, когда существую и равно, т.е. .

Если ф-ция f(x) задана в области Д(у) и в кажд. точке х из Д(у) имеем производную f^/(x), то это значит, что на мн-ве Д(у) определена ф-ция f^/(x), которую наз. производной ф-ции f^/(x), а саму ф-цию f в этом случ. наз. первообразной для ф-ции f^/(x).

Операцию вычисления производной заданной ф-ции f(x) наз. дифференцированием.

Примеры: