1)Описание задачи

2)Определение целей моделирования

3)Анализ объекта или процесса

-изучение теоретических основ и сбор информации об объекте оригинале. Подбирается или разрабатывается подходящая теория, если её нет- устанавливается причина следственной связи между переменными, которые описывают объект. Определяются входные и выходные данные и принимаются упрощающие предположения.

-формализация- выбор системы условных обозначений и устанавливается класс задач к которым может быть отнесена полученная мат модель.

-выбор метода решения- устанавливаются окончательные параметры модели для полученной математической задачи. Выбирается какой-либо метод решения или разрабатывается специальный.

-реализация моделей- пишется программа, которая отлаживается, тестируется и получается решение задачи

-анализ полученной информации- сопоставляется полученное решение и предполагаемое

-проверка адекватности реальному объекту- результаты полученные по модели сопоставляются либо с имеющейся об объекте информацией, либо проводится эксперимент и его результаты сопоставляются с расчётами.

Линейное программирование Постановка задачи линейного программирования

Линейное программирование –наука, о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции на неизвестные которой наложены линейные ограничения. Эта линейная функция называется целевой, а ограничения, которые автоматически записываются в виде уравнений или неравенств называются системой ограничений. Необходимые условия задачи линейного программирования: наличие ограничений на ресурсы, увеличение спроса, производственную мощность и другие производственные факторы. Математическая модель ЗЛП включает:

-максимум или минимум целевой функции

-систему ограничений в форме линейных уравнений и неравенств

-требования не отрицательности переменных

Фирма производит две модели А и Б сборных полок. Их производство ограничено наличием сырья(доски) и времени машинной обработки. Для каждого изделия модели А требуется 3 кв метра досок а для Б 4 кв м. Фирма может получать от своих поставщиков до 1700 кв м в неделю. Для каждого изделия модели А требуются 12 минут машинного времени. А для изделий модели Б- 30 минут. В неделю можно использовать 160 часов машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю, что бы максимизировать прибыль, если каждое изделие модели А приносит 2 доллара прибыли, а Б-4е.

Пусть х1-кол-во полок модели А, а х2-кол-во полок модели Б.

2*х1=прибыль от А

4*х2=прибыль от Б

F(х)=2*х1+4*х2 ->max (целевая функция),

3х1- кол-во досок для А

4х2- кол-во досок для Б

3х1+4х2<=1700 3x1+4x2<=1700

1/5x1+1/2x2<=160 2x1+5x2<=1600

X1=>0;x2=>0

Общий вид: max(min)f(x)=с1*х1+с2*х2+…+сн*хн

A11*x1+a12*x2+…+a1n*xn

A21*x1+a22*x2+…+a2n*xn

…

Am1*x1+am2*x2+..amn*xn

Свойство задач линейно программирования

-допустимое множество решений либо пустое, либо является выпуклым многогранником- пересечение пространств, описываемых неравенствами.

-если допустимое множество не пустое, а целевая функция ограничена снизу, для задачи минимизации и сверху для задачи максимизации, то задачи линейного программирования имеет оптимальные решения.

-оптимальные решения задач линейного программирования всегда находятся на границе допустимого множества, т.е. если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений. Если две или несколько вершин являются оптимальными вершинами, то любая их выпуклая комбинация тоже является оптимальным решением(существует бесконечное множество точек максимума или минимума).

Задача:

При изготовлении изделий и1 и и2 используются токарные и фрезерные станки, а также сталь и цветные металлы. По технологическим нормам требуется 300 и 200 единиц соответственного токарного и фрезерного оборудования в станкочас. 10 и 20 едениц стали и цм металлов в станкочас. Для производства и2 -400, 100, 70, 50 соответствующих ресурсов. Цух располагает 12400,6800 станкочасами оборудования и 640 и 840 стали и цм соответственно. Прибыль от реализации и1-6, и2-16. Определить план выпуска изделий,обеспечивающий максимальную прибыль при условии, что время работы фрезерных станков должно быть использовано полностью.

Ресурсы	И1	И2	Объём ресурсов
Токарные станки	300	400	12400
Фрезерные станки	200	160	6800
Сталь	10	70	640
Цм	20	50	840
Прибыль	6	16

F(x)=6и1+16и2->max

300x1+400x2<=12400

200x1+160x2=6800

10x1+70x2<=640

20x1+50x2<=840

X1>=0,x2>=0

X2=68-2x1

F(x)=1088-26x1

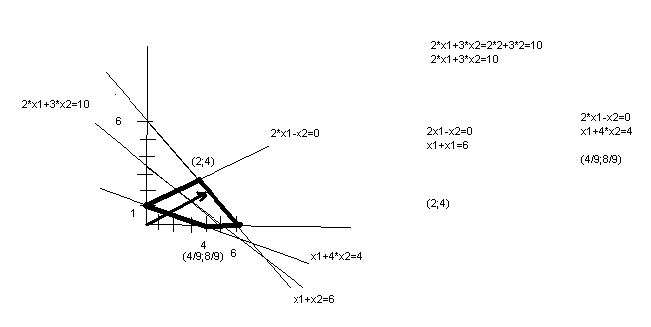
Графический метод решения

Если число неизвестных в задаче линейного программирования(ЗЛП) равняется двем, то её можно решить графическим методом

Max(min) = c1*x1+c2*x2 Bi

X=(x1;x2)

Z=2*x1+3*x2

X1+x2<=6

X1+4*x2>=4

2*x1-x2>=0

X1>=0;x2>=0

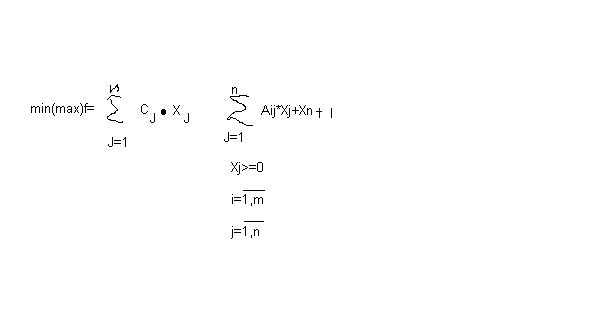
Каноническая форма задачи линейного программирования

Задачи линейного программирования имеют каноническую форму если:

-все ограничения, кроме условия отрицательности переменных, имеют вид строгих равенств, а все свободные члены не отрицательны

Сведём задачу линейного программирования к канонической форме добавив к левым частям системы ограничений дополнительные переменные- Xn+1. В целевую функцию дополнительные переменные вводятся с коэффициентом 0.

Min Z = 2*x1+3*x2

------------

x1+x2=10

-2*x1+3*x2<=-5 (-1)

7*x1-4*x2<=6

x1,x2>=0

------------

------------

x1+x2=10

2*x1-3*x2-0*x3=5

7*x1-4*x2+0*x4=6

x1,x2>=0

------------

Угловая точка с неотрицательным коэффициентом называется опорной. А соответствующий план- опорный план. Базисом опорного плана будем называть систему М линейно-независимых векторов из условия задачи в которую входят все вектора соответствующие не нулевым координатам опорного плана.

Min Z =-5*x1+6*x3

-----------

2*x1-2*x3<=2

2*x1+x2-x3>=3

Xj>=0,j=1..5

----------

-----------

2*x1-2*x3+x4=2

2*x1+x2-x3-x5=3

Xj>=0,j=1..5

----------

Базисная переменная x4 и x5.В целевую функцию не входит знак нуля.

Построение начального опорного плана

Ограничение канонической задачи имеет предпочтительный вид, если при неотрицательности его правой части левая часть содержит переменную входящую с коэффициентом равным единице, а остальные ограничения с коэффициентом равным нулю.

---------

2*x1-2*x3+x4=2

2*x1+x2-x3=3

--------

x0={0;3;0;2}

Если каждое ограничение имеет предпочтительный вид, т.е. система ограничений приведена к единичному неотрицательному базису, то начальный опорный план строится так- предпочтительные переменные выбираются в качестве базисных, а все остальные- свободные. Свободные переменные приравниваются к нулю, а базисные к свободным членам.

Max Z = 2*x1-x3+3*x4+x5

------

X1+4*x3+x4=4

16*x2+x3-2*x4=16

5*x2+x5=6

------

Z(x0)=10

Min Z = 10*x1-7*x2-5*x3+0*x4+0*x5+0*x6

------

6*x1+15*x2+6*x3+x4=9

14*x1+42*x2+16*x3+x5=21

2*x1+8*x2+2*x3+x6=4

------

X0={0;0;0;9;21;4}

Z(x0)=0

Такая система не имеет предпочтительного вида. В этом случае вводят искусственный базис путём перехода к M задаче.

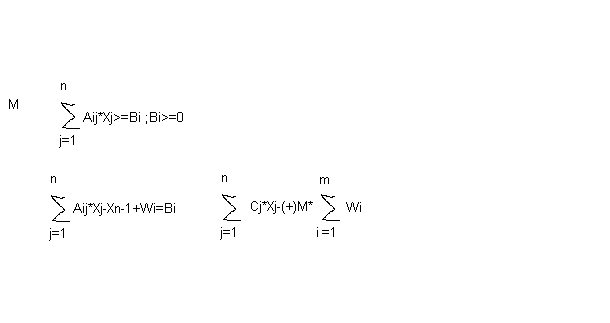
+ ограничение >=

- Ограничение <=

Min Z =-5x1+4*x2+3*x3+6*x4

-----

X1+21*x2+x3+2*x4<=3

-x1-14*x2-2*x3+3*x4>=2

-x1-6*x2+x3-x4>=1

------

-----

X1+21*x2+x3+2*x4+x5=3

-x1-14*x2-2*x3+3*x4-x6=2

-x1-6*x2+x3-x4-x7=1

------

-----

X1+21*x2+x3+2*x4+x5=3

-x1-14*x2-2*x3+3*x4-x6+W1=2

-x1-6*x2+x3-x4-x7+W2=1

------

Min Z =-5x1+4*x2+3*x3+6*x4+0*x5+0*x6+0*x7+M*W1+M*W2

Между оптимальными планами исходной задачи и М задачи имеется следующая связь- если в оптимальном плане М задачи все искусственные переменные Wi=0, то значения оставшихся координат дадут оптимальный план исходной задачи.

Симплексные таблицы

БП	С5	А0	Х1	Х2	Х3	…	Xn
Xn+1	0	B1
Xn+2	0	B2
…	0	Bm
Zj	Cj

Max Z = 18*x1+20*x2+32*x3

----

18*x1+15*x2+12*x3<=720

6+x1+4*x2+8x3<=384

5*x1+3*x2+12*x3<=360

---

----

18*x1+15*x2+12*x3+x4=720

6+x1+4*x2+8x3+x5=384

5*x1+3*x2+12*x3+x6=360

---

Max Z = 18*x1+20*x2+32*x3+0*x4+0*x5+0*x6

БП	С5	А0	Х1	Х2	Х3	X4	X5	X6
X4	0	720	18	20	32	0	0	0
			18	15	12	1	0	0
X5	0	384	6	4	8	0	1	0
X6	0	360	5	3	12	0	0	1
Zj	Cj	0	-18	-20	-32	0	0	0

Рабочая область таблицы начиная с 3его столбца и 3й строки содержит элементы расширенной матрицы над которыми будут проводиться преобразования с целью получения оптимального плана. В последней строке таблицы записано нулевое уравнение эта строка называется индексной строкой или строкой оценок. Индексная строка заполняется по формуле:

J= Сб*Аj-Cj

0*18+0*6+0*5-18

В столбце бп занесены базисные переменные. В столбце сб содержит элементы целевой функции стоящие при базисных переменных. Столбец а0 при базисных переменных содержит свободные элементы системы ограничений. Сверху над рабочей частью таблицы указаны все переменные и коэффициенты целевой функции.

Min Z = -6*x1+8*x2-x3+2*x4

----

-2*x1+x2+x3=8

3*x1-8*x2+x4=48

----

БП	С5	А0	Х1	Х2	Х3	X4
X3	-1	8	-6	8	-1	2
			-2	1	1	0
X4	2	48	3	-8	0	1
Zj	Cj	88	14	-25	0	0

D0= -1*8+2*48=88

D1=-1*(-2)+2*3-(-6)=14

D2=-25

D3=0

D4=0

X0={0;0;8;48}

----

Х1+х2+х3=12

Х2+х4=2

2*x1+x2+x5=20

----

Max Z = 2*x1+4*x2+0*x3+0*x4+0*x5

БП	С5	А0	Х1	Х2	Х3	X4	X5
X3	0	12	2	4	0	0	0
			1	1	1	0	0
X4	0	2	0	1	0	1	0
X5	0	20	2	1	0	0	1
Zj	Cj	0	-2	-4	0	0	0

БП	С5	А0	Х1	Х2	Х3	X4	X5
X3	0	10	2	4	0	0	0
			1	0	1	-1	0
X2	4	2	0	1	0	1	0
X5	0	18	2	0	0	-1	1
Zj	Cj	8	-2	0	0	4	0

X3A0(2)=(X3A0(1)* X4X2(1)-X2A0(1)*X3X2(1))/X4X2(1)

БП	С5	А0	Х1	Х2	Х3	X4	X5
X3	0	1	2	4	0	0	0
			0
X2	4	2	0
X1	2	9	1	0	0	-1/2	1/2
Zj	Cj	26	0	0	0	3	1

X*- оптимальное значение

X*=(9;2;1;0;0)

Алгоритм симплекс методов:

-используя каноническую форму определяем начальный опорный план

-строим симплексную таблицу, проверяем критерий оптимальности задачи на максимум, если в полученной таблице все элементы полученной таблицы не отрицательны, то такой план оптимален

-критерий оптимальности задачи на минимум- если в полученной таблице все элементы нижней троки не положительны, то такой план оптимален

-переходим к выбору разрешающего элемента- элемента, стоящего на пересечении разрешающей строки и столбца

-в задаче на минимум в качестве разрешающего столбца берём столбец, содержащий максимальный положительный элемент нижней строки

-в задаче на максимум- максимальный по модулю отрицательный элемент

-в качестве разрешающей строки берём строку, к которой отношение элементов столбца свободных членов А0 к соответствующему элементу разрешающего столбца минимальной соответствующий элемент должен быть положительный

Min{ Bi/Aik}

-строим новую таблицу, в которой заменяем базисную переменную на переменную разрешающего столбца

-осуществляем следующие преобразования- элементы разрешающей строки делим на разрешающий элемент. Элементы разрешающего столбца заменяются нулями. Вместо разрешающего элемента пишется единица. Все остальные элементы новой таблицы находятся по правилу прямоугольника- произведение главной диагонали( содерж разрешающий элемент) минус побочная диагональ и делить на разрешающий элемент.

Решение может быть не одно. Если в нижней строке последней симплексной таблицы имеется хотя бы 1н нулевой элемент соответствующий свободной переменной, то задача линейного программирования имеет бесконечное множество решений.

Признак пустого множества решений. Если в разрешающем столбце нет положительный элементов, то решений нет.

Метод искусственного базиса

В системе переменная Хn+I образуют искусственный базис. Получение максимального опорного плана исходной задачи основано на следующих утверждениях:

-если в оптимальном плане М задачах все искусственные переменные равны нулю, то план является оптимальным

-если в ОП по крайней мере одна из искусственных переменных положительна, то исходная задача не имеет ни одного плана

-если М задачи не имеет решения, то исходная задача не разрешима

В симплексных таблицах для функции F отводится две строки. Одну для f, другую для М. Если преобразования выполняются с двумя строками, то признак оптимальности сначала проверяется сначала по 2й строке. По ней же проверяются переменные, включаемые в базис. Процесс преобразования продолжается до тех пор, пока из базиса не исключены все искусственные переменные. По мере исключения из базиса этих переменных соответствующие им столбцы можно опускать.

f= -2*x1-6*x2+5*x3-x4-4*x5 (max)

-----

X1-4*x2+2*x3-5*x4+9*x5=3

X2-3*x3+4*x4-5*x5=6

X2-x3+x4-x5=1

-----

X1- так как не входит в след два

-----

X1-4*x2+2*x3-5*x4+9*x5=3

X2-3*x3+4*x4-5*x5+х6=6

X2-x3+x4-x5+х7=1

-----

Задача на максимум, значит в целевую ф они входят с -М

f= -2*x1-6*x2+5*x3-x4-4*x5-М(х6+х7)

x1=3+4*x2-2*x3+5*x4-9*x5

x6=6-x2+3*x3-4*x4+5*x5

x7=1-x2+x3-x4+x5

f= -2*(3+4*x2-2*x3+5*x4-9*x5)-6*x2+5*x3-x4-4*x5-М((6-x2+3*x3-4*x4+5*x5)+( 1-x2+x3-x4+x5

))= -6-8*x2+4*x3-10*x4+18*x5-6*x2+5*x3-x4-4*x5-M(7-2* x2+4*x3-5*x4+6*x5)=

=-6-14*x2+9*x3-11*x4+14*x5-M(7-2* x2+4*x3-5*x4+6*x5)

БП	С5	А0	Х2	Х3	Х4	X5	БП		С5		А0		Х2		Х3		X5
X1	-2	3	-4	2	-5	9	X1		-2		8		1		-3		4
X6	-4	6	1	-3	4	-5	X6		-4		2		3		1		-1
X7	7	1	1	-1	1	-1	X7		7		1		1		-1		-1
F		-6	14	-9	11	-14	F				-11		3		2		-3
	M	-7	2	4	-5	6			M		-2		3		-1		1
БП	С5	А0	Х2	Х5				БП		С5		А0		Х2		Х3		X5
X1		14	-8	2				X5				14
X3		2	-2	-1				X3				1
X4		1	-2	-1				X4				31
F		-21	9	-1				F				-7		1		0