
- •Остальные аналогично.
- •Остальные аналогично.
- •Вопрос 9.
- •Вопрос 10.
- •Вопрос 11.
- •Вопрос 12.
- •Вопрос 13. Понятие локального экстремума. Необходимое условие локального экстремума.
- •Вопрос 14. Достаточное условие локального экстремума.
- •Вопрос 15. Понятие условного экстремума. Метод множителей Лагранжа. Необходимое условие условного экстремума.
- •Вопрос 16 Достат. Усл-я условного экстремума.
- •Вопрос 17.
- •Вопрос 18
- •Вопрос19
- •Вопрос 20
- •Вопрос 22
- •Вопрос 24
- •Вопрос 25. Геометрические приложения двойных интегралов а) вычисление площадей б) вычисление объемов в) вычисление площадей поверхностей
- •Вопрос 26. Тройной интеграл. Переход к повторному интегралу (без д-ва). Замена переменных (без д-ва), цилиндрич. И сферич. Система координат.
- •Вопрос 28. Криволинейный интеграл 2-го рода; его свойства.
- •Вопрос 30. Независимость криволинейного интеграла от пути интегрирования.
- •Вопрос 34. Ортогональная тригонометрическая система. Ряд Фурье для абсолютно интегрируемой на [-;] ф-ции; ряд Фурье для четной и нечетной ф-ции. Ряд Фурье в случае произвольного интервала.
Вопрос 22
Двойной интеграл. Теорема об интегрируемости непрерывной функции двух переменных (без доказательства). Свойства двойного интеграла. Теорема о среднем.
z = f(x,y)
, (x,y)
= f(x,y)
, (x,y)
![]() G, где G –
замкнутая область.
G, где G –
замкнутая область.
![]() - частичная обл.
- частичная обл.
![]() - площади обл.
- площади обл.
![]() .
.
![]()
![]() - интегральная сумма.
- интегральная сумма.
Опр.Диаметром
![]() частичной области
частичной области
![]() называется максимальная длина хорды
этой частичной области.
называется максимальная длина хорды
этой частичной области.
Если![]()
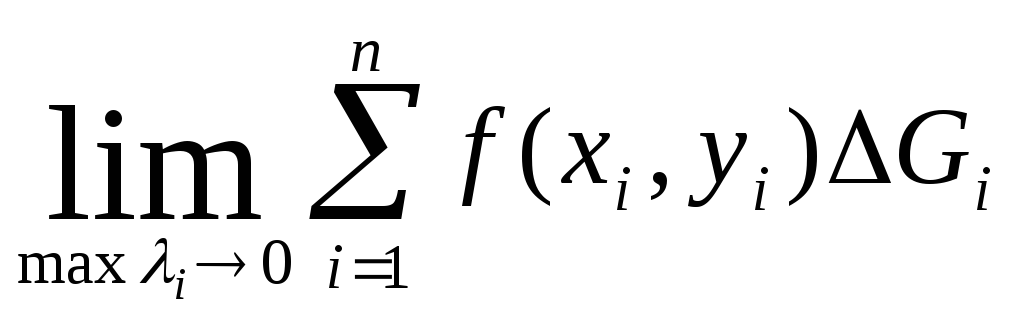 ,
не зависящий от разбиения области G
и от выбора промежуточных точек
,
не зависящий от разбиения области G
и от выбора промежуточных точек
![]() ,
то этот предел называется двойным
интегралом функции f(x,y)
по области G.
,
то этот предел называется двойным
интегралом функции f(x,y)
по области G.![]() ,
,
![]()
Теорема(об интегрируемости непрерывной
функции двух переменных) Пусть f(x,y)
непрерывна в области G.
Тогда она интегрируема в этой области,
т.е.
![]()
Свойства двойного интеграла.
1о. Аддитивность.Если функция f(x,y) интегрируема в области G и если область G при помощи кривой T площади нуль разбивается на две связные и не имеющие общих внутренних точек области G1 и G2, то функция f(x,y) интегрируема в каждой из областей G1 и G2, причём
![]()
2о. Линейное свойство.Если
функции f(x,y)
и g(x,y)
интегрируемы в области G,
а
![]() и
и
![]() - любые вещественные числа, то функция
- любые вещественные числа, то функция
![]() также интегрируема в области G,
причём
также интегрируема в области G,
причём
![]() .
.
3о. Если функции f(x,y) и g(x,y) интегрируемы в области G, то и производные этих функций интегрируемы в G.
4о. Если f(x,y) и g(x,y) обе интегрируемы в области G и всюду в этой области f(x,y) ≤ g(x,y), то
![]() .
.
5о. Если функция f(x,y)
интегрируема в области G,
то и функция |f(x,y)|
интегрируема в области G,
причём
![]() .
.
Теорема о среднем значении.Если обе функции f(x,y) и g(x,y) интегрируемы в области G, функция g(x,y) неотрицательна (неположительна) всюду в этой области, M и m – точная верхняя и точная нижняя грани функции f(x,y) в области G, то найдётся число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула
![]() .
.
В частности, если функция непрерывна в G, а область G связна, то в этой области найдётся такая точка (ξ,η) что μ=f(ξ,η), и формула принимает вид
![]() .
.
Интеграл
![]() равен площади области G.
равен площади области G.
Вопрос № 23
Приведение двойного интеграла к повторному (а) случай прямоугольной области, б) случай области более общего вида). Двойной интеграл в полярных координатах.
а) случай прямоугольной области
Теорема Пусть для функции f(x,y)
в прямоугольнике
![]() существует двойной интеграл
существует двойной интеграл
![]() .Пусть
далее для каждого x из
сегмента
.Пусть
далее для каждого x из
сегмента
![]() существует однократный интеграл
существует однократный интеграл
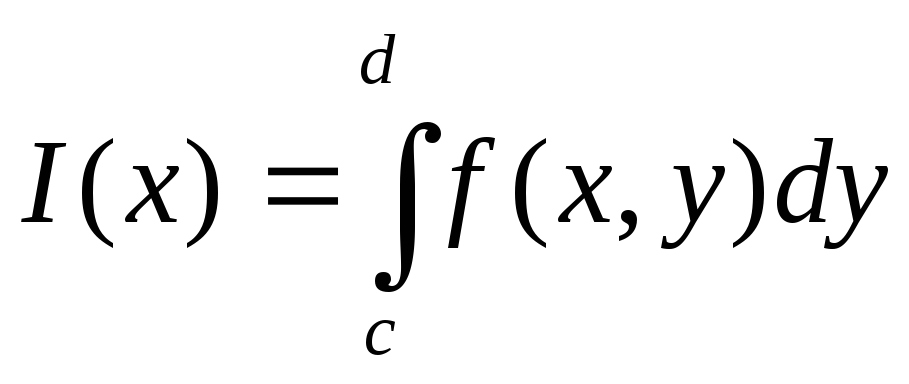 .Тогда
существует повторный интеграл
.Тогда
существует повторный интеграл
 и справедливо равенство
и справедливо равенство
![]() .
.
Доказательство.
Разберём прямоугольник R
с помощью точек
![]() и
и
![]() на n·p
частичных прямоугольников
на n·p
частичных прямоугольников
![]() (k=1,…,n;l=1,…,p).
(k=1,…,n;l=1,…,p).
Положим
![]() ,
,
![]() и обозначим через
и обозначим через
![]() и
и
![]() точные грани функции f(x,y)
на частичном прямоугольнике
точные грани функции f(x,y)
на частичном прямоугольнике
![]() .
.
Тогда всюду на этом прямоугольнике
![]() .
.
Положим в этом неравенстве
![]() ,
где
,
где
![]() - произвольная точка сегмента
- произвольная точка сегмента
![]() ,
и после этого проинтегрируем
,
и после этого проинтегрируем
![]() по y в пределах от
по y в пределах от
![]() до
до
![]() .
Получим
.
Получим
 .
(1)
.
(1)
Суммируя (1) по всем
![]() от 1 до p и используя
обозначение
от 1 до p и используя
обозначение
![]() ,
будем иметь
,
будем иметь
![]() .
(2)
.
(2)
Далее умножим (2) на
![]() и просуммируем по всем k
от 1 до n. Получим
и просуммируем по всем k
от 1 до n. Получим
![]() .
(3)
.
(3)
Пусть наибольший диаметр
![]() частичных прямоугольников стремится
к нулю. Тогда наибольшая из длин
частичных прямоугольников стремится
к нулю. Тогда наибольшая из длин
![]() стремится к нулю. Обрамляющие члены в
(3), представляющие собой нижнюю и верхнюю
суммы, стремятся при этом к двойному
интегралу
стремится к нулю. Обрамляющие члены в
(3), представляющие собой нижнюю и верхнюю
суммы, стремятся при этом к двойному
интегралу
![]() .
Стало быть, существует предел и среднего
члена в (3), равный тому же самому двойному
интегралу. Но этот предел по определению
однократного интеграла равен
.
Стало быть, существует предел и среднего
члена в (3), равный тому же самому двойному
интегралу. Но этот предел по определению
однократного интеграла равен
 .
Тем самым доказано существование
повторного интеграла и равенство
.
Тем самым доказано существование
повторного интеграла и равенство
![]() .
Теорема доказана.
.
Теорема доказана.
б) случай области более общего вида
Теорема
Пусть выполнены следующие условия:
1) область D ограничена,
замкнута и такова, что любая прямая,
параллельная оси Oy,
пересекает границу этой области не
более чем в двух точках, ординаты которых
![]() и
и
![]() ,
где
,
где
![]() ;
;
2 )
функция f(x,y)
допускает существование двойного
интеграла
)
функция f(x,y)
допускает существование двойного
интеграла
![]() и существование для любого x
однократного интеграла
и существование для любого x
однократного интеграла
 .
.
При этих условиях существует повторный интеграл
 (
(![]() и
и
![]() - наименьшая и наибольшая
- наименьшая и наибольшая
абсциссы точек области D)
и справедливо равенство
 .
.
Доказательство.
Обозначим через R
прямоугольник со сторонами, параллельными
координатным осям, содержащий область
D, а через F(x,y)
– функцию, совпадающую с f(x,y)
в точках области D и равную
нулю в остальных точках R.
Для функции F(x,y)
выполнены в прямоугольнике R
все условия теоремы, и, стало быть,
справедлива формула
![]() ,
которая (с учётом того, что F(x,y)
равна нулю вне D и совпадает
с f(x,y)
в D) переходит в формулу
,
которая (с учётом того, что F(x,y)
равна нулю вне D и совпадает
с f(x,y)
в D) переходит в формулу
 .
.
Д войной
интеграл в полярных координатах.
войной
интеграл в полярных координатах.
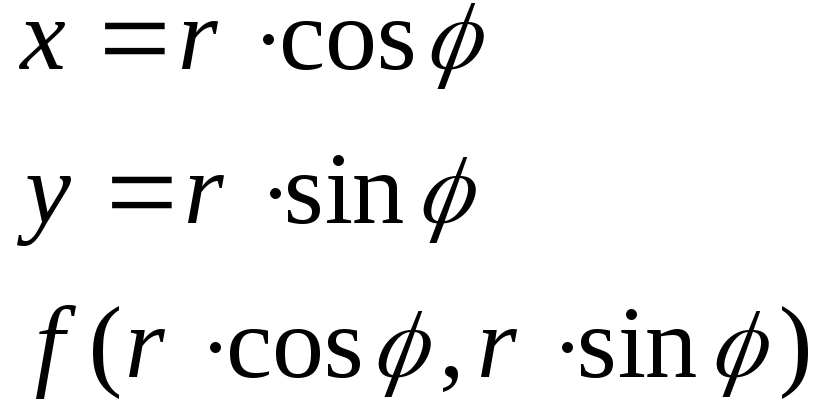

![]()
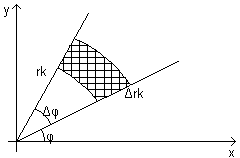
![]()


![]()
![]()

