Билет 1

Предел последовательности точек пространства Rⁿ.(?) Лемма о сходимости последовательности точек в пространстве Rⁿ; фундаментальная последовательность точек в Rⁿ. Лемма о фундаментальной последовательности; критерий Коши сходимости последовательности точек пространства Rⁿ. Теорема Больцано - Вейерштрасса.

Опр: n – мерным координатным пространством называется совокупность всех упорядоченных наборов вида (х₁, х₂, … , х_n), где х_i є R, i = 1 … n.

х = (х₁, …, х_n), у = (у₁, …, у_n) …

Опр: Последовательностью точек в пространстве Rⁿ, называется отображение множества натуральных чисел в пространстве Rⁿ (т.е N -> Rⁿ).

х₁ -> х⁽¹⁾ = (х₁⁽¹⁾, х₂⁽¹⁾, … ,х_n⁽¹⁾) … х_к -> х^(к) = (х₁^(к), х₂^(к), … ,х_n^(к))

Опр: Последовательность {х^(к)} є Rⁿ сходится к точке х⁽⁰⁾ Rⁿ, если для ε > 0  N: для к ≥ N выполняется (х^(к), х⁽⁰⁾) < ε т.е. . ()

Лемма о сходимости последовательности точек в пространстве Rⁿ: Последовательность {х^(к)} є Rⁿ сходится к точке х⁽⁰⁾ Rⁿ <=> каждая из числовых последовательностей {х₁^(к)}, {х₂^(к)}, …, {х_n^(к)} сходится соответственно к числам х₁⁽⁰⁾, х₂⁽⁰⁾, …, х_n⁽⁰⁾.

Доказательство:

1)

2)

- - - - - - - - - -

N = max {N₁, N₂, …, N_n} следовательно

Опр: Последовательность {х^(к)} є Rⁿ называется фундаментальной, если для

Лемма о фундаментальной последовательности: Последовательность {х^(к)} є Rⁿ является фундаментальной (последовательностью Коши) <=> каждая из последовательностей {х₁^(к)}, {х₂^(к)}, …, {х_n^(к)} является фундаментальной.

Доказательство:

1) {х^(к)} – фундаментальная последовательность => (по определению) для , следовательно

2) {х₁^(к)} – фундам. посл. =>

{х₂^(к)} – фундам. посл. =>

- - - - - - - - - -

{х_n^(к)} – фундам. посл. =>

N = max {N₁, N₂, …, N_n} следовательно => {х^(к)} – фундаментальная последовательность.

Критерий Коши сходимости последовательности точек пространства Rⁿ: Последовательность {х^(к)} є Rⁿ сходится <=> она является фундаментальной.

Доказательство:

1) Последовательность {х^(к)} фундам. => {х^(к)} – сходится

{х^(к)} – фундам. => {х_i^(к)} (i = 1…n) - фундам. => - противоречие (по кр. Коши сходимости числовой последовательности).

2) {х_i^(к)} сходится к точке х⁽⁰⁾ => {х_i^(к)} сходится к числу х_i⁽⁰⁾, i = 1…n => {х_i^(к)} (i = 1…n) – фундам. => {х^(к)} – фундаментальная последовательность.

Опр: Последовательность {х^(к)} є Rⁿ называется ограниченной, если и для

Доказательство:

{х^(к)} є Rⁿ

Пусть k₁, k₂, …, k₃, … - произвольная строго возр. Последовательность

x^(k1), x^(k2), …, x^(ki), …

{х^(ki)} – подпоследовательность последов. {х^(к)}

{х^(ki)} < {х^(k)}

Теорема Больцано – Вейерштрасса: Из любой ограниченной в Rⁿ последовательности {х^(k)} можно выделить сходящуюся подпоследовательность.

Доказательство:

{х^(к)} – ограниченная в Rⁿ посл. => т.е. => для вып. => {х_i^(k)} – ограниченная числовая последовательность, i = 1…n

=>

, ,

- - - - - - - - - -

Следовательно {х₁^(kin)}, {х₂^(kin)}, …, {х_n^(kin)} – сходящиеся подпоследовательности.

Билет 2

Предел функции n переменных в точке по Гейне и по Коши, эквивалентность этих определений. Арифметические операции над функциями, имеющими предел. Бесконечно малые функции n переменных.

Опр. предела по Гейне: Функция f(x₁, …, x_n) имеет в точке x⁽⁰⁾ = (x₁⁽⁰⁾, …,x_n⁽⁰⁾) предел, равный b, если для {x^(k)} и т.е

Опр. предела по Коши: Функция f(x₁, …, x_n) имеет в точке x⁽⁰⁾ = (x₁⁽⁰⁾, …,x_n⁽⁰⁾) предел, равный b, если для

,

Эквивалентность определений по Гейне и по Коши: Пусть b – предел функции f(x) в точке x⁽⁰⁾ по Гейне => b – предел функции по Коши.

Доказательство:

1) Пусть b – не является пределом функции f(x) по Коши т.е. такое, что

Пусть , тогда

Получаем , =>

2) Пусть b – предел функции f(x) в точке x⁽⁰⁾ по Коши => b – предел функции по Гейне.

b – предел функции по Коши => для => =>

Арифметические операции над функциями, имеющими предел: Пусть и , тогда:

1. 

2. 

3. 

Доказательство:

1. выполняется ,

2. Остальные аналогично.

Опр: Функция f(x) называется бесконечно малой в точке x⁽⁰⁾, если

Утв: Пусть , тогда

Доказательство:

Обозначим

=>

Следовательно => т.е.

Билет 3

Критерий Коши существования предела функции n переменных в точке.

Опр: Функция f(x) удовлетворяет условию Коши в точке x⁽⁰⁾, если для

Критерий Коши существования предела функции в точке: Функция f(x) имеет предел в точке x⁽⁰⁾ <=> она удовлетворяет условию Коши в этой точке.

Доказательство:

1) Пусть => f(x) удовлетворяет условию Коши в точке x⁽⁰⁾ =>

Пусть

Следовательно

2) Функция f(x) удовлетворяет условию Коши в точке x⁽⁰⁾ =>

Пусть =>

Функция f(x) удовлетворяет условию Коши в точке x⁽⁰⁾ =>

Для

Для

Следовательно

Для => =>

Пусть

Пусть b = b’, тогда

Следовательно

Билет 4

Повторные пределы. Теорема о существовании повторного предела.

f(x₁, …, x_n); ; u = f(x, y); |x - x₀| < d₁, |y – y₀| < d₂

Опр: Пусть для любого фиксированного y: |y – y₀| < d₂ , тогда

Теорема о существовании повторного предела: Функция u = f(x, y): |x - x₀| < d₁, |y – y₀| < d₂

1. 

2. Для

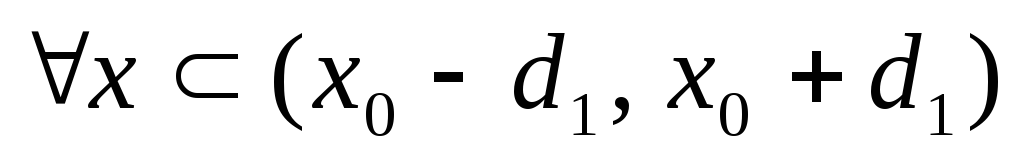
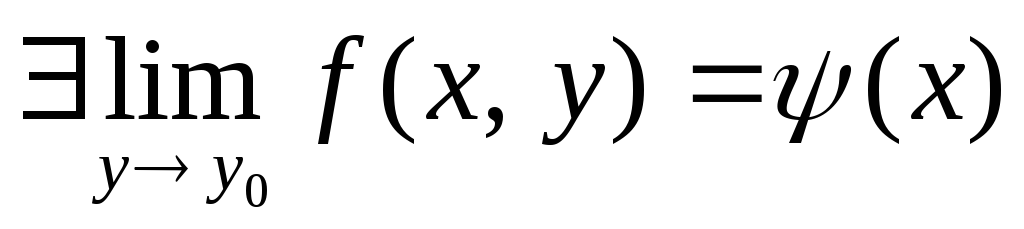
Тогда

Доказательство:

Т.к. => выполняется . Следовательно

=> => =>

Отсюда для =>

Зам: Для , тогда

Билет 5

Непрерывность функции нескольких переменных в точке. Арифметические операции над непрерывными функциями. Непрерывность сложной функции. Теорема об устойчивости знака непрерывной в точке функции. Теорема о прохождении непрерывной функции через любое промежуточное значение.

Опр (формальное): Функция y = f(x) = f(x₁, x₂, …, x_n) непрерывна в точке x⁽⁰⁾ = (x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_n⁽⁰⁾), если

Опр 1: Функция f(x) непрерывна в точке x⁽⁰⁾, если для и

Опр 2: Функция f(x) непрерывна в точке x⁽⁰⁾, если для

Доказательство:

y = f(x) = f(x₁, x₂, …, x_n), x⁽⁰⁾ = (x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_n⁽⁰⁾) => y = f(x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_k, …, x_n⁽⁰)

Если , то f(x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_k, …, x_n⁽⁰⁾) – непрерывна по k-той переменной.

Теорема: Пусть функция f(x) непрерывна в точке x⁽⁰⁾, тогда f(x) непрерывна в точке x⁽⁰⁾ по каждой переменной.

Доказательство:

Функция f(x) непрерывна в точке x⁽⁰⁾ =>

f(x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_k, …, x_n⁽⁰⁾) => для => f(x) непрерывна в точке x⁽⁰⁾ по каждой переменной.

Арифметические операции над непрерывными функциями:

Функции f(x) и g(x) непрерывны в точке x⁽⁰⁾ = (x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_n⁽⁰⁾) =>

1. 

2. 

3. 

Доказательство:

1. , тогда

2. Остальные аналогично.

Непрерывность сложной функции:Функция y = f(x₁, x₂, …, x_n) непрерывна в точке x⁽⁰⁾ = (x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_n⁽⁰⁾) т.е. тогда

Доказательство:

Функция f(x₁, x₂, …, x_n) непрерывна в точке x⁽⁰⁾ =>

=>

Т.е.

=>

Т.е.

- - - - - - - - - -

=>

Т.е.

тогда все в порядке

Теорема об устойчивости знака… : Функция y = f(x₁, x₂, …, x_n) непрерывна в точке x⁽⁰⁾ = (x₁⁽⁰⁾, x₂⁽⁰⁾, …, x_n⁽⁰⁾), => существует окрестность точки x⁽⁰⁾ в которой функция сохраняет свой знак.

Доказательство:

Функция f(x₁, x₂, …, x_n) непрерывна в точке x⁽⁰⁾ => т.е. => - окрестность точки x⁽⁰⁾ в которой функция сохраняет свой знак.

Теорема о прохождении … через промежуточное значение: Функция y = f(x₁, x₂, …, x_n) непрерывна во всех точках связанной области Q точки : f(A) и f(B) – значения функции в точках A и B.

Пусть C – любое число заключенное между f(A) и f(B), тогда на любой непрерывной кривой найдется точка .

Доказательство:

Пусть L – непрерывная кривая соединяющая точки A и B.

- непрерывные функции переменной ; значении функции на концах отрезка соответствуют значениям функции f(A) f(B).

A = (a₁, …, a_n), B = (b₁, …, b_n): ,

- непрерывная функция на отрезке

, => => => функция проходит через промежуточное значение C.

Билет 6

Первая теорема Вейерштрасса (об ограниченности функции, непрерывной на компакте).

Опр: Компакт – ограниченное замкнутое множество

Первая теорема Вейерштрасса: Пусть f(x₁, …, x_n) непрерывна на ограниченном замкнутом множестве Q, тогда f(x₁, …, x_n) – ограничена на множестве Q.

Доказательство:

Пусть f(x₁, …, x_n) не является ограниченной на Q функцией => для ; ;

Т.к. f(x) непрерывна на Q . Следовательно => f(x₁, …, x_n) является ограниченной на Q функцией.

Билет 7

Вторая теорема Вейерштрасса (о достижении непрерывной на компакте функцией своих точных граней).

Опр: Число называется верхней гранью функции f(x), если:

1. Для

2. Для (?)

Для нижней грани аналогично.

Вторая теорема Вейерштрасса: Функция f(x₁, …, x_n) непрерывная на ограниченном замкнутом множестве Q достигает своих верхней и нижней граней.

Доказательство:

Пусть f(x₁, …, x_n) не достигает своей верхней грани на множестве Q => для

Рассмотрим вспомогательную функцию ; F(x) – определена и непрерывна в => по первой теореме Вейерштрасса F(x) – ограничена т.е. ; ; ; => - не является верхней гранью.

Билет 8

Равномерная непрерывность функции нескольких переменных.(?) Теорема Кантора о равномерной непрерывности функции, непрерывной на компакт**

Опр: Функция f(x) равномерно непрерывна на множестве Q, если для для

Теорема Кантора: Функция непрерывная и ограниченная на компакте равномерно непрерывна на нем.

Доказательство:

f(x₁, …, x_n) непрерывна на компакте Q.

Пусть f(x₁, …, x_n) не является равномерно непрерывной на Q =>

;

=>

; =>

.

Следовательно для -противоречие т.к. => f(x₁, …, x_n) - равномерно непрерывна на компакте.