30.Общие сведения о случайных функциях и процессах.

Случайная функция - функция произвольного аргумента t (заданная на множестве Т его значений и сама принимающая или числовые значения или, более общо, значения из какого-то векторного пространства) такая, что её значения определяются с помощью некоторого испытания и в зависимости от его исхода могут быть различными, причём для них существует определённое распределение вероятностей. Если множество Т конечно, то С. ф. представляет собой конечный набор случайных величин, который можно рассматривать как одну векторную случайную величину. Из числа С. ф. с бесконечным Т наиболее изучен важнейший частный случай, когда t принимает числовые значения и является временем; соответствующая С. ф. X (t) тогда называется случайным процессом (а если время t пробегает лишь целочисленные значения, то также и случайной последовательностью, или временным рядом). Если же значениями аргумента t являются точки из некоторой области многомерного пространства, то С. ф. называется случайным полем. Типичными примерами С. ф., отличных от случайных процессов, являются поля скорости, давления и температуры турбулентного течения жидкости или газа, а также значения высоты z взволнованной морской поверхности или поверхности какой-либо искусственной шероховатой пластинки.

         Математическая теория С. ф. совпадает с теорией распределений вероятностей в функциональном пространстве значений функции X (t), эти распределения могут задаваться набором конечномерных распределений вероятностей для совокупностей случайных величин X (t₁), X (t₂),..., X (t_n), отвечающих всевозможным конечным подмножествам (t₁, t₂,..., t_n) точек множества Т, или же характеристическим функционалом С. ф. X (t), представляющим собой математическое ожидание случайной величины il [X (t)], где l [X (t)] — линейный функционал от Х (t) общего вида. Значительное развитие получила теория однородных случайных полей, являющихся частным классом С. ф., обобщающим класс стационарных случайных процессов.

Случайный процесс (вероятностный, или стохастический) -  процесс (т. е. изменение во времени состояния некоторой системы), течение которого может быть различным в зависимости от случая и для которого определена вероятность того или иного его течения. Типичным примером С. п. может служить Броуновское движение

31. Характеристики случаных функций.

Хар-ки СФ предст-ют собой определенные ф-ции: M[x], D[x], КФ.

Мат. ожидмнием СФ x(t) наз-ют такую неслучайную ф-цию mx(t), кот. при каждом допустимом зн-нии аргумента равна МО ординаты: mx(tj)=M[x(tj)]. Т. е. МО представляет собой среднюю функцию, отн-но кот. группируются возможные реализации СФ.

Дисперсией СФ x(t) наз-ют такую неслучайную ф-цию Dx(t), кот. при каждом допустимом зн-нии аргумента (t=tj) равна дисперсии ординат в этой точке: Dx(t)=D[x(tj)]. Дисперсия СФ неотрицательная ф-ция. Арифметическое зн-ние квадратного корня из дисперсии наз-ся средним квадратическим отклонением: .

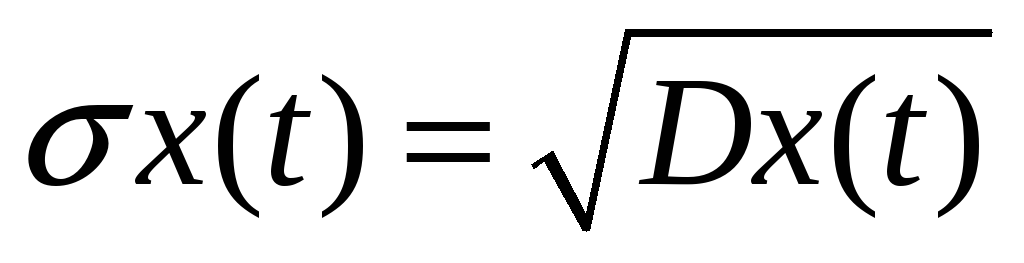Ср. квадр. отклонение СФ при каждом t хар-ет средний разброс реализаций СФ отн-но МО. МО и дисперсия – важные хар-ки СФ, но для описания основных особенностей СФ этих хар-к недостаточно. Хар-к изменения СФ м. б. различен, а МО и дисперсия одинаковы. Для более полного описания СФ применяют КФ, кот. опр-ет момент между двумя зн-ями аргумента. Кор. ф-цией СВ наз-ют неслучайную ф-цию, кот. при каждой паре допустимых зн-ний аргумента равен КМ ординат, центрированных отн-но МО. Т. к. КМ СВ не зависит от последовательности, в кот. рассм-тся аргумент, то и КФ не меняется при перемене аргумента местами. Kx(tj, ti)=Kx(ti, tj).