
- •2.1. Решающие поверхности и дискриминантные функции
- •2.2. Линейные дискриминантные функции
- •2.2.1. Общая форма лдф
- •2.2.2. Классификация по минимуму расстояния
- •2.2.3. Линейная разделимость
- •2.3. Кусочно-линейные дискриминантные функции (клд)
- •2.3.1.Определение клд и правило ближайшего соседства
- •Случай 3.
- •2.4.Нелинейные дискриминантные функции
- •2.5.2. Емкость φ-машин для классификации образов.
- •2.6. Потенциальные функции как дф
2.2. Линейные дискриминантные функции
Как было рассмотрено ранее, дискриминантная функция позволяет разделить в пространстве образов различные классы путем построения разделяющих поверхностей.
Дискриминантные функции могут быть линейными и нелинейными в зависимости от типа задачи.
В этом разделе мы рассмотрим общую форму линейной дискриминантной функции (ЛДФ) и затем применим ее к построению классификатора по минимуму расстояния. Также будет рассмотрено понятие линейной разделимости.
2.2.1. Общая форма лдф
ЛДФ может быть представлена в следующей форме:
dk(Х) = wk1*x1+wk2*x2+………. wкn*xn+ wк,n+1*xn+1
или в матричной форме
dk(Х)
= Wkт*Х
, где
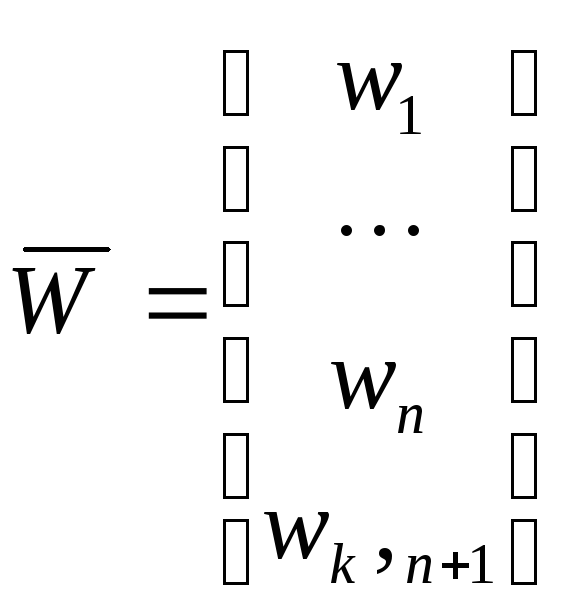 ,
,
 ,
,
и хn+1 = 1 в рассмотренном векторе образа.
Для 2-х классовой задачи М=2
d(Х) = w1т*x +w2т*x = (w1 -w2)т*x = 0
представляет собой гиперплоскость проходящую через 0 в расширенном пространстве признаков.
2.2.2. Классификация по минимуму расстояния
Хотя этот классификатор был предложен достаточно давно, до сих пор он остается эффективным инструментом решения задачи классификации.
Решающее правило, используемое в этом методе, имеет вид:
x![]() Wj
, если D(x, zj)=
Wj
, если D(x, zj)=![]() D(x, zk), k=1,…M
D(x, zk), k=1,…M
где D(°) — метрика, называемая евклидовым расстоянием образа х от zk, и zk — есть эталонное среднее (или центр класса) для класса Wk.
Тогда
D(x, zk) = |x - zk|
Исходя из D(x, zk)
> D(x, zj)
![]() j,k
j,k
Имеем
D2(x, zk) > D2(x, zj)
Другими словами, мы можем использовать D2 вместо D в решающем правиле:
D2(x, zk) = |x - zk|2
Или в матричной форме
D2(x, zk) = (x - zk)т (x - zk) = хтх –2хт zk + zkт zk
Учитывая, что выражение хтх является постоянной для всех к, его можно отбросить. Тогда поиск минимума D(x, zk) эквивалентен поиску
![]() [–2хт
zk + zkт zk]
[–2хт
zk + zkт zk]
или альтернативно мы должны найти
![]() [хт
zk - ½zkт zk], к=1,2,…М
[хт
zk - ½zkт zk], к=1,2,…М
Последнее выражение определяет классификатор по минимуму расстояния. ДФ, используемая в классификаторе, может быть выражена как
dk(Х) = хт zk - ½zkт zk = хт zk - ½ |zk|2 = хт W
где
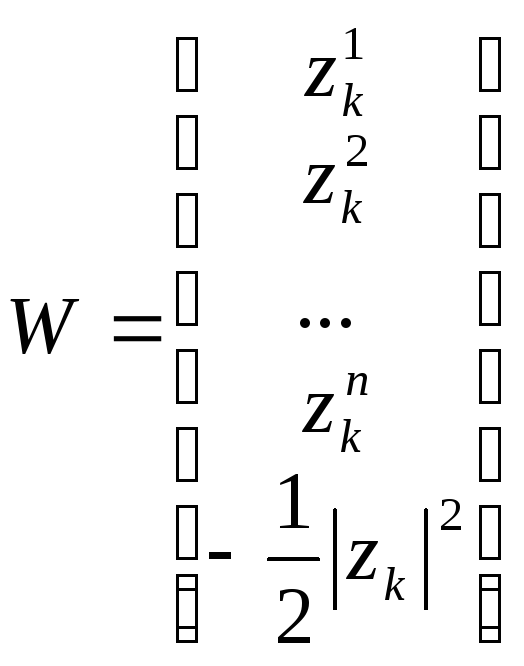
и
![]() —
расширенный вектор
—
расширенный вектор
Отметим, что решающая поверхность между любыми двумя классами Wi и Wj образуется плоскостью, перпендикулярной линии zi - zj, проходящей через ее середину.

Рис.
Доказательство этого очень просто.
Уравнение решающей поверхности классами W1 и W2 имеет вид
d(Х) = хт (z1 – z2 ) - ½(z1т z1 – z 2т z2 =0
Возьмем точку — середину отрезка, соединяющего z1 , z2
![]()
Подставим zср в выражение d(x)
![]()
Очевидно, сама гиперплоскость, разделяющая W1 и W2 определяется вектором нормали:
![]()
Отметим, что классификатор по минимуму расстояния использует для представления каждого класса одну точку.
Такое представление будет справедливым для случая нормального распределения с равными дисперсиями по каждой координате, как показано на рис.2.6а
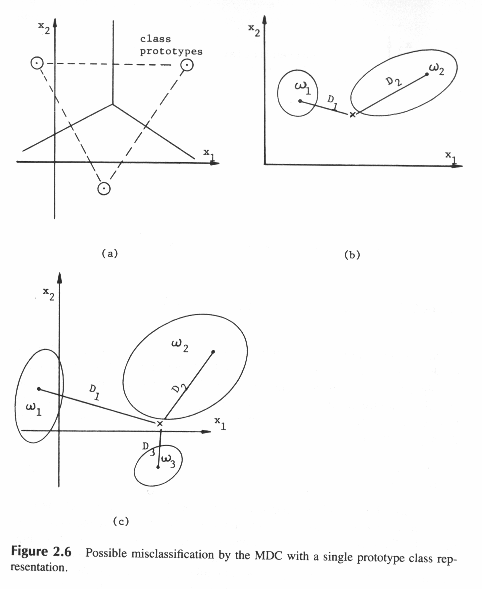
рис.2.6
Однако в случае, если классы не будут нормально распределенными с одинаковыми дисперсиями по всем координатам, как показано на рис.2.6.b, то будет иметь место неправильная классификация.
Даже если D1 < D2, точка + должна быть отнесена к W2 вместо W1. Аналогично, на рис.2.6с точка + должна быть отнесена к W3 по минимуму расстояния, однако она ближе кW2.
Т.о., представление класса одной точкой не является хорошим решением. Если представить каждую категорию образов с помощью мультипрототипов, вместо единичного прототипа, тогда
D(x, Wk)=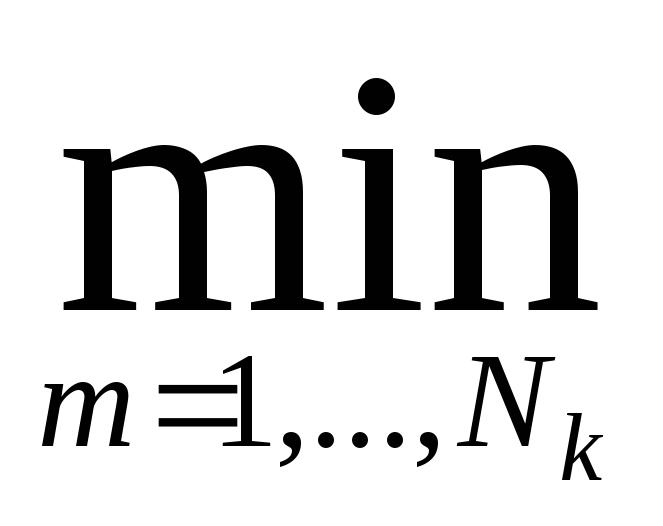 [
D(x, zkm)],
(2.21)
[
D(x, zkm)],
(2.21)
Где к представляет к-ую категорию, m — номер m-го прототипа, Nк — число прототипов для категории к.
Это уравнение дает наименьшее расстояние между Х и каждым прототипом из Wk.
Тогда решающее правило становится таким
x
![]() Wj,
если D(x, Wj)=
Wj,
если D(x, Wj)=![]() [
D(x, Wk)],
[
D(x, Wk)],
где D(x, Wk) дается выражением (2.21)
ДФ изменяется соответственно так
dk(Х)
=
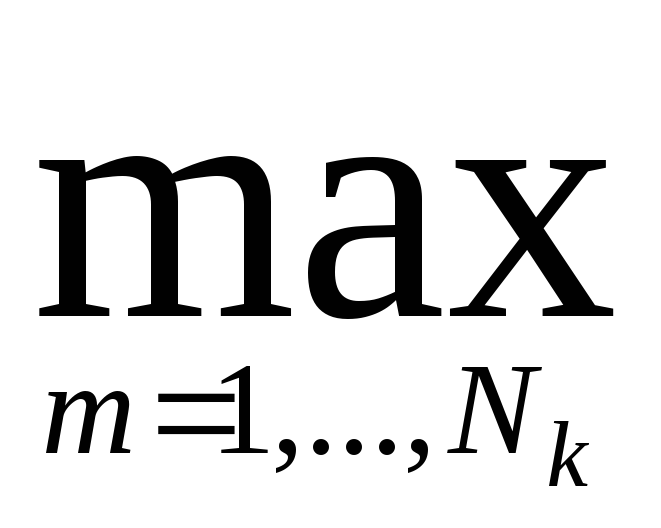 [хт
zkm -
½|zkm|2],
к=1,2,…М
[хт
zkm -
½|zkm|2],
к=1,2,…М
