Теория автоматов относится к числу ключевых разделов современной кибернетики. Она непосредственно связана с математической логикой, теорией алгоритмов, теорией формальных грамматик. Универсальность и сравнительная простота автоматов обусловили широкое использование автоматных моделей на практике. Теория автоматов, например, успешно используется при построении узлов цифровых вычислительных машин; при построении программ и, в частности, лексических анализаторов в трансляторах.
Абстрактная теория автоматов выделяет два основных способа использования автоматов: преобразование входной последовательности символов в выходную (синтез дискретных устройств) и проверка правильности входной последовательности символов (синтез программных анализаторов).
В данных методических указаниях дана краткая теоретическая справка, а также приведены примеры синтеза и эквивалентных преобразований автоматов.
Для закрепления знаний приведены упражнения, для некоторых из них даны решения.
Структурный синтез автоматов и вопросы их практического использования будут рассматриваться в последующих курсах, связанных с цифровыми вычислительными машинами.
ПОНЯТИЕ АВТОМАТА
Автоматом называют дискретный преобразователь информации, который принимает входные сигналы (буквы) в дискретные моменты времени и с учетом своего прежнего состояния формирует выходные сигналы и изменяет свое состояние.
Автомат есть система
U=<X,Y,Q,f (q, x), ϕ (q, x) >,
где X={x1, x2, …, xn} – входной алфавит;
Y={y1, y2, …, ym} - выходной алфавит;
Q={q0 ,q1, …, qs} - алфавит внутренних состояний;
f (q, x): Q∗X→Q – функция переходов;
ϕ (q, x):Q∗X→Y – функция выходов.
Часто фиксируют также начальное состояние автомата q0∈Q. Такие ав-
томаты называют инициальными (будем рассматривать только инициальные
автоматы).
Законы функционирования автоматов:
а) для автоматов первого рода (автоматов Мили)
q ( t ) = f ( q ( t-1 ), x ( t )),
y ( t ) = ϕ ( q ( t-1 ), x ( t ));
б) для автоматов второго рода
q ( t ) = f ( q ( t-1 ), x ( t )),
y ( t ) = ϕ ( q ( t ), x ( t ));
в) для правильных автоматов второго рода (автоматов Мура)
q ( t ) = f ( q ( t-1 ), x ( t )),
y ( t ) = ϕ ( q ( t )).
Примеры.1. Построить (синтезировать) автомат, на вход которого могут
поступать в любой последовательности и, возможно, с любым числом повторе-
ний монеты 1,2 и 3 коп. Автомат продает билет, если сумма опущенных монет
равна 3. В случае превышения суммы автомат возвращает деньги.
Входной алфавит в описании задан явно: X={1,2,3}.
Выходной алфавит будет содержать буквы (сигналы): Б- выдает билет,
В- возвращает деньги, Н- ничего не выдает, т.е. Y{Н,Б,В}.
Внутренние состояние будем отождествлять с суммой, которую помнит
автомат. Будем иметь в виду, что после продажи билета или возврата денег
автомат помнит нулевую сумму: Q={q0, q1, q2}, здесь индекс соответствует сум-
ме.
Автомат в виде графа представлен на рис. 1.
Рисунок 1
Это автомат Мили. Надпись 1/Б; 2,3/В у стрелки q2q0 означает, что если в состоянии q2 будет принят сигнал 1, выходной сигнал будет Б, а для входных сигналов 2 и 3 выходным будет В. Этот же автомат можно представить в виде двух таблиц: таблицы переходов (табл.1) и таблицы выходов (табл.2).
Таблица 1 Таблица 2
Текст файла Автоматы Пермь
2. Построить автомат, на вход которого могут поступать монеты 1, 2 и 3 коп. Автомат выдает сигнал “чет.” (Ч), если сумма опущенных монет четная, и “нечет.” (Н), если нечетная (рис.2).
Рисунок 2.
q0 q1 q2
1 q1 q2 q0
2 q2 q0 q0
3 q0 q0 q0
q0 q1 q2
1 Н Н Б
2 Н Б В
3 Б В В
Сумма 0 считается четной. Это автомат Мура, т.е. его выходной сигнал
однозначно определяется состоянием, в которое автомат перешел, поэтому вы-
ходные сигналы приписаны прямо к состояниям. Этот же автомат можно пред-
ставить отмеченной таблицей переходов (табл.3 ).
Таблица 3
Н Ч
qн qч
1 qч qн
2 qн qч
3 qч qн
Автомат называется частичным, если некоторые комбинации
“состояние– входной сигнал” не могут возникнуть в реальных условиях. При
этом в графе автомата появляются состояния, из которых определены выходы
не для всех входных сигнаов (т.е. присутствуют не все стрелки), а в таблицах
переходов и выходов (и в отмеченной таблице переходов) имеются
незаполненные клеточки.
Для выполнения эквивалентных преобразований, как и для структурного
синтеза, необходимо доопределить частичный автомат. Переходы и выходы
обычно доопределяют, исходя из соображений удобства минимизации.
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ АВТОМАТОВ
Два атомата называются эквивалентными, если они имеют одинаковые
входные и выходные алфавиты и на одинаковые входные слова выдают
одинаковые выходные слова.
Переход от автомата Мили
К эквивалентному автомату Мура
Законы функционирования автоматов Мили и Мура отличаются функци-
ей выходов. Поскольку каждой паре ”состояние – входной сигнал” автомата
Мили может соответствовать свой выходной сигнал, а в автомате Мура
выходной сигнал приписываенся состоянию, то каждой паре qi x j автомата
Мили ставится в соответствие состояние синтезируемого автомата Мура b i j.
Таким образом, каждой клеточке таблицы переходов автомата Мили бу-
дет соответствовать новое состояние автомата Мура. Кроме того, поскольку
первый выходной сигнал автомат выдаст, когда из начального состояния под
воздействием первого входного сигнала перейдет в какое-то состояние, которое
и определит первый выходной сигнал, то необходимо для автомата Мура ввести
также начальное состояние b0, которому может быть приписан любой допусти-
мый выходной сигнал. Поскольку функции переходов у автоматов Мили и Му-
ра одинаковы, каждому состоянию автомата Мили ставится в соответствие
класс изоморфных состояний автомата Мура. Технику установления соответст-
вий рассмотрим на примере.
Пример. Возьмем ранее рассмотренный автомат Мили (см. табл. 1 и 2).
Перерисуем табл. 1, указав в клеточках i j состояния bij синтезируемого
автомата Мура (табл. 4). Попав в любое из таких состояний, автомат Мура дол-
жен обеспечить дальнейшую реализацию прежней функции переходовтолько
уже в ”терминах” состояний автомата Мура, т.е. состояния b0, b03, b12, b13, b21, b22,
и b23 должны обеспечить переходы, аналогичные тем, которые имели место для
состояния q0 в автомате Мили, b01 -аналогичное q1, а b02 и b11-аналогичные q2.
Полученный автомат Мура приведен в табл. 5.
Пусть не смущает, что автомат получился явно избыточным, уменьшить
число состояний- дело техники. Главное, что он ”работает” точно так же, как и
исходный автомат Мили.
Таблица 4
Таблица 5
Таким образом, существует стандартный прием, с помощью котороко
можно преобразовать автомат Мили в эквивалентных ему автомат Мура. При-
чем, если в автомате Мили n внутренних состояний и m входных то в получен-
ном автомате Мура будет n∗ m+1 состояний.
Переход от автомата Мура
К эквивалентному автомату Мили
Из анализа переходов автоматов Мили и Мура следует, что для перехода
от автомата Мили к автомату Мура необходимо как бы отнести каждый выход-
ной сигнал к предшествующему состоянию и входному сигналу, который пере-
вел автомат Мура в данное состояние. Другими словами, на графе автомата вы-
ходные сигналы, ранее приписанные вершинам, необходимо отнести ко всем
заходящим в эту вершину дугам. Например, для автомата рис. 2 эквивалентный
автомат Мили будет иметь вид, показанный на рис.3.
Рис. 3
Н Н Б Н Б В Б В В
b0 b01 b02 b03 b11 b12 b13 b21 b22 b23
1 b01 b11 b21 b01 b21 b01 b01 b01 b01 b01
2 b02 b12 b22 b02 b22 b02 b02 b02 b02 b02
3 b03 b13 b23 b03 b23 b03 b03 b03 b03 b03
q0
b0
q1 q2
1 q1
b01
q2
b11
q0
b21
2 q2
b02
q2
b12
q0
b22
3 q3
b03
q0
b13
q0
b23
Не менее просто осуществляется переход для автомата, заданного в таб-
личной форме. Это можно увидеть, если для рис. 3 нарисовать соответствую-
щие таблицы переходов и выходов (табл. 6 и 7).
Таблица 6 Таблица 7
В этом случае таблица переходов дублирует существующую, а таблица
выходов получается заменой в таблице переходов состояний, в которые перехо-
дит автомат, на выходные сигналы, которые этим состояниям были приписаны
в автомате Мура.
МИНИМИЗАЦИЯ АВТОМАТОВ
Минимальный автомат- это автомат, имеющий наименьшее возможное
количество состояний и реализующий заданную функцию выходов.
Два состояния автомата называются 1-эквивалентными, если, находясь в
любом из этих состояний, автомат на один и тот же входной сигнал (входное
слово длиной в 1) выдает один и тот же выходной сигнал. Два состояния авто-
мата называются К- эквивалентными, если, начиная с любого из этих состояний,
автомат на любые одинаковые слова длины К выдает одинаковые выходные
слова (также длины К). Если два состояния К- эквивалентны для любых К, то их
называют (просто) эквивалентными. Множество попарно эквивалентных со-
стояний образует класс эквивалентности.
Смысл _______минимизации состоит в выявлении классов эквивалентности и
замене каждого класса одним состоянием.
Процедура минимизации состоит в следующем:
1. По таблице выходов автомата Мили (или по первой строке отмечен-
ной таблице переходов автомата Мура) находятся состояния, имею-
щие одинаковые столбцы (отмеченные одинаковыми выходными
сигналами) – это 1-эквивалентные состояния.
2. Далее используется таблица переходов. Все состояния, входящие в 1-
эквивалентный класс, которые под воздействием первого сигнала пе-
решли в состояния, принадлежащие в свою очередь 1-
эквивалентному классу, образуют 2-эквивалентный касс.
3. Процедура разбиения на классы эквивалентности продолжается до те
пор, пока при очередном шаге К- эквивалентные классы не совпадут
с (К-1)-эквивалентными, т.е. получатся эквивалентные классы.
4. Все состояния, входящие в один класс эквивалентности, заменяются
одним состоянием.
Пример. Рассмотрим автомат Мили заданный табл. 8 и 9.
qн qч
1 qч qн
2 qн qч
3 qч qн
qн qч
1 ч н
2 н ч
3 ч н
Таблица 8 Таблица 9
1 – эквивелентные классы определяются из табл. 8 , 2 – эквивалентные из
табл. 9 , а 3 – эквивалентные _______и просто эквивалентные из табл. 10 .
Таблица 10 Таблица 11 Таблица 12
В качестве имен состояний минимального автомата возьмем име-
на классов. Минимальный автомат представлен табл. 11 и 12.
РАСПОЗНАЮЩИЕ АВТОМАТЫ
Распознающий автомат – это автомат Мура, в котором фиксируется на-
чальное состояние и подмножество состояний F⊆Q, называемое множеством
заключительных состояний. Говорят, что автомат допускает (принимает, распо-
знает, представляет) данное слово, если реакцией на это слово может быть пе-
реход автомата в одно из заключительных состояний.
Примеры. 1. Автомат (рис. 4) с начальным состоянием 1 и заключитель-
ным F1 и F2 допускает слова, в которых имеются только парные вхождения букв
a и b, например, a a, a a a a a a, b b a a и т.д.
Рис. 4
2.Для распознавания часто используются частичные автоматы (рис.5),
допускающие тоже множество слов, что и автомат, показанный на рис.4.
1 2 3 4 5 6
x1 y1 y1 y1 y1 y1 y2
x2 y2 y2 y2 y2 y2 y2
1 2 3 4 5 6
x1 1
α
4
α
6
β
2
α
6
β
4
α
x2 2
α
1
α
3
α
2
α
5
α
5
α
α β γ
x1 α γ α
x2 α β β
α β γ
x1 y1 y1 y2
x2 y2 y2 y2
1 2 4 3 5 6
x1
1
α
4
α
2
α
6
γ
6
γ
4
α
x2
2
α
1
α
2
α
3
β
5
β
5
β
α β α β α β γ
Рис. 5 Рис. 6
Здесь начальное состояние 1, а заключительное F. Слово считается недо-
пустимым, если в результате реакции на него автомат не остановится в заклю-
чительном состоянии или если будет подан запрещенный (для данного состоя-
ния) входной сигнал. Например, воздействие входного слова ab на автомат вы-
зовет переход в состояние 2 по букве a , но в этом состоянии не определен пере-
ход по букве b , следовательно, слово ab недопустимо. Если считать пустое (не
содержащее ни одной буквы) слово допустимым, то можно еще более упростить
частичный автомат, объединив начальное и заключительное состояния (рис.6).
3.Одним из наиболее широко используемых на практике типов распо-
знающих автоматов является частичный недетерминированный автомат. Неде-
терминизм проявляется в том, что из одного состояния по одному и тому же
входному сигналу возможны переходы в различные состояния, т.е. функция пе-
реходов заменяется отношением переходов. Недетерминированный автомат
(рис.7) принимает, например, слова ab, aa, bb, bba и т.д. здесь начальное со-
стояние A, а заключительное -F.
Рис. 7
Таблица переходов данного автомата будет иметь вид табл.13.
Таблица 13
A B C F
a B,C F
b B C,F
Пустые клеточки говорят о том, что автомат частичный, а наличие сразу
нескольких букв в одной клеточке – о том, что автомат недетерминированный.
Для таких автоматов обычно предпочитают использовать не табличное и не
графовые представления, а запись в виде так называемых продукций или грам-
матических правил, представленных в двух столбцах соответственно:
A → aB A:: = aB / bB / aC
A → bb B:: = bC / b
A → aC C:: = a
B → bC
B → b
C → a
Такого рода грамматики называют регулярными, или автоматными.
Автоматы такого типа будут рассмотрены в связи с изучением теории
формальных языков и грамматик.
УПРАЖНЕНИЯ
Звездочками отмечены задания, для которых приводятся решения.
1.Построить (синтезировать) автомат по содержательному описанию.
1.1.∗ На вход автомата могут поступать сигналы R, S и T. На входной
сигнал R автомат выдает выходной сигнал 0, на S- выходной сигнал 1 и на T-
выходной сигнал, противоположный предыдущему выходному сигналу. Для
определенности считаем, что в начальном состоянии автомат помнит
’’предыдущий’’ выходной сигнал 0 .
1.2.∗ Автомат имеет две входные шины X1 и X2 , на которые в дискретные
моменты независимо друг от друга могут поступать сигналы 0 или 1. В автома-
те вычисляется функция f=x1 ⊕ x2, а затем определяется, сколько раз с учетом
данного момента времени функция f принимала значение 1. Выходной сигнал Y
может иметь три значения:
Y = 0,если f = 0;
Y = 1,если f = 1 и суммарное число случаев, включая данный, когда f
равнялась единице, нечетно;
Y = 2 в остальных случаях.
1.3.∗Автомат управляет светофором на перекрестке дорог ”вертикальная
- горизонтальная”. Считается, что при открытом светофоре (зеленом свете) ма-
шины преодолевают перекресток мгновенно. Светофор переключается (мгно-
венно), если число ожидающих машин с обеих сторон перпендикулярной улицы
достигло трех.
1.4.∗ На вход автомата могут поступать символы, допустимые в языке
ПЛ/1. Автомат выдает сигнал U, если на вход поступил идентификатор, в про-
тивном случае выдает сигнал Н. Считаем, что идентификатор впереди и сзади
ограничен пробелами.
1.6.∗ Автомат Мура, принимая на входе монеты 10; 15 и 20 коп., выдает
сигнал П, если значение текущей суммы опущенных монет кратно 50 и не крат-
но 1 руб.; выдает сигнал Р, если сумма кратна 1 руб.; во всех остальных случаях
выдает сигнал 0.
1.20* На вход автомата по двум шинам x1 и x2 поступают различные
комбинации из нулей и единиц, воспринимаемые как двоичные числа. Автомат
выдаёт сигнал Н , если сумма поступившых чисел нечётная, К - если сумма
чисел кратная четырём, и 4 – если сумма чисел чётная, но не кратна четырём.
2. * Привести примеры автоматов:
2.1 имеющих два внутренних состояния;
2.2 имеющих одно внутренних состояние;
2.3 не имеющих ни одного внутреннего состояния.
3. Придумать автомат, имеющий не менее трёх и не более пяти
состояний.
4. Преобразовать автомат Мили в автомат Мура:
4.1 Таблица 14 Таблица 15
5. Преобразовать автомат Мура в автомат Мили:
5.1 * Таблица 24
7. Минимизировать автомат Мили:
7.1 * Таблица 30 Таблица 31
7.2 * Таблица 32 Таблица 33
q0 q1 q2
x1 q1 q0 q2
x2 q2 q1 q1
q0 q1 q2
x1 y2 y1 y3
x2 y4 y5 y6
y1 y2 y3
q1 q2 q3
x1 q2 q3 q3
x2 q1 q2 q3
0 1 2 3 4 5 6
x1 1 3 4 6 6 6 6
x2 2 4 5 4 5 3 0
0 1 2 3 4 5 6
x1 y1 y3 y3 y1 y1 y1 y1
x2 y2 y2 y2 y2 y2 y2 y2
1 2 3 4 5 6 7 8 9
α 2 1 2 3 6 8 6 4 7
β 2 4 2 2 4 9 2 4 9
γ 5 4 5 2 3 6 8 7 7
1 2 3 4 5 6 7 8 9
α 1 0 1 0 1 0 1 1 0
β 1 1 1 1 1 1 1 1 1
γ 1 1 1 1 1 1 1 1 1
8. Минимизировать автомат Мура.
8.1* Таблица 44 8.2* Таблица 45
9. Синтезировать распознающий автомат, описываемы регулярной
(автономной) грамматикой.
9.1.*На вход могут поступать символы, допустимые в языке ПЛ/1. Авто-
мат распознаёт идентификаторы (без ограничения по длинне).
9.2.*Автомат распознаёт десятичные константы с фиксированной точ-
кой, допустимые в ПЛ/1.
9.5.*Автомат распознаёт условный оператор ПЛ/1 , которыё имеет вид:
IF е THEN t1 [ELSE t2]
Считаем, что на этом этапе анализа ключевые слова языка, а также вы-
ражения е и группы операторов t1 и t2 заменены отдельными символами.
Квадратные скобки говорят о том, что соответствующий фрагмент может отсут-
ствовать.
11.. Для недетерминированного автомата, заданного грамматическими
правилами, построить эквивалентный детерминированный автомат.
11.1.* А ::= ab / aC 11.2. A ::= ab / bB / aC
B ::= b B ::= bc / b
C ::= a C ::= a
12. Придумать свои упражнения, аналогичные приведённым, и выпол-
нить их.
РЕШЕНИЯ.
1.1. Соответствующий автомат Мура представлен на рис. 8.
Рис. 8
y1 y2 y1 y1 y1 y1 y2
1 2 3 4 5 6 7
x1 1 2 3 4 1 2 1
x2 5 5 5 2 7 2 2
y1 y1 y2 y2 y1 y1 y2
a b c d e f g
x1 d g g d d c g
x2 a b b b b a b
x3 e b b g g d d
1.2. Каждой комбинации значений х1 и х2 припишем букву (рис. 9).
Автомат Мили представлен на рис. 10.
Рис. 9 Рис. 10
1.3. В данном автомате по два входных сигнала соответствуют подходу
к перекрёстку одной машины по вертикальной (сигнал В) и горизонтальной
(сигнал Г) дорогам. Поскольку учитывается только общее число машин на дан-
ной дороге независимо от того, с какой стороны они подходят, общий перечень
состояний, которые должен различать автомат, будет соответствовать рис. 2.
Рис. 2
Так, например, состояние 2 говорит о том, что светофор открыт для вертикаль-
ной дороги, а на горизонтальной ожидает одна машина. Жирные черточки, со-
ответствующие положения светофора, возьмем в качестве символов сигналов
( │ , ─ ). Автомат представлен табл.14.
Таблица 14.
1.4. Примем обозначения: б – буква, ц – цифра, - пробел, π – любой
другой входной символ, ~ - выходной сигнал «неопределённо». Автомат Мура
может иметь вид рис. 12 (длину идентификатора не ограничиваем).
x1 x2
A 0 0
D 0 1
C 1 0
D 1 1
1 2 3 4 5 6
▬
▬
▬
▬ ▬ ▬
1 2 3 4 5 6
В 1 2 3 5 6 1
Г 2 3 4 4 5 6
рис. 12 рис 13.
П р и м е ч а н и е . Для данного содержательного описания частичный
недетерминированный распознающий автомат может иметь вид рис. 13, где
1 – начальное состояние, а F –заключительное. Соответствующая автоматная
грамматика может быть записана как:
1 ::= б / б2
2 ::= б2 / ц2 / б / ц
1.6. Этот «безобидный» с виду автомат требует, судя по всему, 21 со-
стояния. Не полностью ( для наглядности) заполненная табл.15 ил-
люстрирует возможное решение. Начальное состояние 0 использу-
ется только на первом шаге. Следует обратить внимание на появле-
ние состояния 5.
Таблица 15
О О О О О О О О О О П О О О О О О О О О Р
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
х10 10 15 20 50 100 5 10
х15 15 20 50 100 5 10 15
х25 20 50 100 5 10 15 20
Но это первое приходящее в голову решение. А может быть, можно по-
строить более компактный автомат Мура?
1.20. Решение может иметь вид рис. 14.
Рис. 14
1.2.. Наиболее ходовые примеры – это одноразрядные двоичные элемен-
ты памяти (хранящие один бит информации): триггер, ферритовое кольцо, реле
и т.п.
2.2.. Фактически, это автоматы без памяти, может служить любая комби-
национная схема.
2.3.. Автомат без состояния не имеет смысла.
4.1.. Результирующий автомат Мура будет иметь вид табл. 16.
Таблица 16
5.1.. Результирующий автомат Мили будет иметь вид табл. 17, 18.
Таблица 17 Таблица 18
7.1. Определим 1-эквивалентные классы, используя таблицу выходов, и с
помощью таблицы переходов определим 2-эквивалентные классы (табл.19). Оп-
ределение 3-эквивалентных классов показано в табл.20.
Таблица 19 Таблица 20
▬ y2 y4 y1 y5 y3 y6
b0 b01 b02 b11 b12 b21 b22
x1 b01 b11 b21 b01 b11 b21 b11
x2 b02 b12 b22 b02 b12 b32 b22
q1 q2 q3
x1 q2 q3 q3
x2 q1 q2 q3
q1 q2 q3
x1 y3 y2 y2
x2 y1 y3 y2
0 1 2 3 4 5 6
х1
1
b
3
a
4
a
6
a
6
a
6
a
6
a
х2
2
b
4
a
5
a
4
a
5
a
3
a
0
a
0 1 2 3 4 5 6
х1
1
b
3
c
4
c
6
c
6
c
6
c
6
c
х2
2
b
4
c
5
c
4
c
5
c
3
c
0
c
a b c a b c
a b c a b c d
Определим далее 4-эквивалентные классы (табл. 21). 3-эквивалентные классы
совпали с 4-эквивалентными, следовательно, мы получили классы эквивалент-
ных состояний. Минимальный автомат будет иметь вид табл. 22 и 23.
0 1 2 3 4 5 6
х1
1
b
3
c
4
c
6
d
6
d
6
d
6
d
х2
2
b
4
c
5
c
4
c
5
c
3
c
0
a
Таблица 21
Таблица 22 Таблица 23
7.2. Минимальный автомат будет иметь вид табл.24, 25.
Таблица 24 Таблица 25
Отметим, что _______при различном кодирование классов эквивалентности
можно получить не абсолютно одинаковые, а изоморфные (т.е. одинаковые с
точностью до имен состояний) автоматы.
8.1. 1-эквивалентные классы определяются по первой строке отмеченной
таблицы переходов, 2-эквивалентные – на основе содержания этой таблицы
(табл.26).
y1 y1 y1 y1 y1 y1 y1
1 2 3 4 5 6 7
a b c d
х1 b c d d
х2 b c c a
a b c d
х1 y1 y3 y1 y1
х2 y2 y2 y2 y2
a b c d e
α c d a a b
β c c c e e
γ b a c d b
a b c d e
α 1 1 0 0 0
β 1 1 1 1 1
γ 1 1 1 1 1
a b c d
a b
a b c d
x1
1
a
2
a
3
a
4
a
1
a
2
a
1
a
x2
5
a
5
a
5
a
2
a
7
b
2
a
2
a
Таблица 26
В результате выполнения всех возможных разбиений (табл.27, 28, 29)
получим минимальный автомат Мура (табл.30).
Таблица 27 Таблица 28
Таблица 29 Таблица 30
Обратим внимание на то важное обстоятельство, что используемая про-
цедура минимизации в ряде случаев может быть ”излишне” универсальной. Она
не учитывает того, что мы рассматриваем лишь инициальные автоматы.
(Начальное состояние во всех примерах, независимо от использования
различных систем обозначения, в таблицах всегда идет первым). А например,
для инициального автомата с начальным состоянием а (см. табл. 30)
невозможен переход в состояние с, т.е. состояние с является недостижимым.
Следовательно, его можно исключить. Из исходного автомата можно убрать
недостижимые состояния до начала процесса минимизации. (Существуют и
другие ”аномальные” ситуации. Какие, на ваш взгляд?).
1 2 3 4 5 6 7
х1
1
a
2
a
3
a
4
a
2
a
1
a
1
a
х2
5
b
5
b
5
b
2
a
2
a
7
c
2
a
1 2 3 4 5 6 7
х1
1
a
2
a
3
a
4
b
2
a
1
a
1
a
х2
5
c
5
c
5
c
2
a
2
a
7
d
2
a
1 2 3 4 5 6 7
х1
1
a
2
a
3
a
4
b
2
a
1
a
1
a
х2
5
d
5
d
5
d
2
a
2
a
7
e
2
a
y1 y1 y1 y1 y2
a b c d e
x1 a b a a a
x2 d a a e a
a b a c
a b c a b c d
a b c d a b c d e
a b c d e
a b c d e
8.2. Минимальный автомат представлен табл. 31.
y1 y1 y2 y2 y1 y1
α β γ ε η δ
x1 ε ε ε ε ε γ
x2 α β β β β α
x3 η β β ε ε ε
Таблица 31
9.1. См. рис.13 и соответствующее примечание.
9.2. В ПЛ/1 константы с фиксированной точкой могут иметь один из сле-
дующих видов:
а) S a1 … an · b1 … bn
б) S a1 … an
в) S a1 … an
г) S· b1 … bm
где S – либо пусто, либо + или - ; ai (i = 1,n) – цифры целой части, bj (j = 1,m) –
цифры дробной части.
Распознающий автомат можно представить в виде рис.15, где А- началь-
ное, а F – заключительное состояние.
Рис.15
Однако этот распознающий автомат не дает регулярной
грамматики (из заключительного состояния есть выходящая
стрелка). Для получения регуляр- ной грамматики введем
дополнительное состояние (рис.16).
Рис.16
Соответствующая грамматика будет:
А : : = u C |+ B |– B |+ D |– D |· D |u E |u
B : : = u C |·D
D : : = u E | u
E : : = u E | u
9.5. См. рис.17. Считаем, что t1 и t2 заканчивается символом : .
Рис.17
10.1. См. рис.18.
Рис.18
11.1. A : : = a D
D : : = a / b
СПИСОК ЛИТЕРАТУРЫ
1. Глушков В.М. Синтез цифровых автоматов. – М.: Физматгиз, 1962.
2. Гилл А. Введение в теорию конечных автоматов. – М.: Наука, 1966.
3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для
инженеров. – М.: Энергия, 1960.
4. Вавилов Е.Н., Портной Г.П. Синтез схем электронных цифровых ма-
шин. – М.: Советское радио, 1963.
5. Бузунов Ю.А., Вавилов Е.Н. Принципы построения цифровых вычис-
лительных машин. Киев: Техника, 1972.__
Конечные автоматы |
Содержание
Два наиболее распространенных способа конечного задания формального языка - это грамматики и автоматы. Автоматами в данном контексте называют математические модели некоторых вычислительных устройств. В этой лекции рассматриваются конечные автоматы, соответствующие в иерархии Хомского праволинейным грамматикам. Более сильные вычислительные модели будут определены позже, в лекциях 10, 14 и 15. Термин "автоматный язык" закреплен за языками, распознаваемыми именно конечными автоматами, а не какими-либо более широкими семействами автоматов (например, автоматами с магазинной памятью или линейно ограниченными автоматами). В разделе 2.1 определяются понятия конечного автомата (для ясности такой автомат можно называть недетерминированным конечным автоматом) и распознаваемого конечным автоматом языка. В следующем разделе дается другое, но эквивалентное первому определение языка, распознаваемого конечным автоматом. Оно не является необходимым для дальнейшего изложения, но именно это определение поддается обобщению на случаи автоматов других типов. В разделе 2.3 доказывается, что тот же класс автоматных языков можно получить, используя лишь конечные автоматы специального вида (они читают на каждом такте ровно один символ и имеют ровно одно начальное состояние). Во многих учебниках конечными автоматами называют именно такие автоматы. Целую серию классических результатов теории формальных языков составляют теоремы о точном соответствии некоторых классов грамматик некоторым классам автоматов. Первая теорема из этой серии, утверждающая, что праволинейные грамматики порождают в точности автоматные языки, доказывается в разделе 2.4. Другая серия результатов связана с возможностью сузить некоторый класс грамматик, не изменив при этом класс порождаемых ими языков. Обычно в таком случае грамматики из меньшего класса называются грамматиками в нормальной форме. В разделе 2.5* формулируется результат такого типа для праволинейных грамматик. Сама эта теорема не представляет большого интереса, но аналогичные результаты, доказываемые позже для контекстно-свободных грамматик, используются во многих доказательствах и алгоритмах. Не все конечные автоматы подходят для конструирования распознающих устройств, пригодных для практических приложений, так как в общем случае конечный автомат не дает точного указания, как поступать на очередном шаге, а разрешает продолжать вычислительный процесс несколькими способами. Этого недостатка нет у детерминированных конечных автоматов (частного случая недетерминированных конечных автоматов), определенных в разделе 2.6. В разделе 2.7 доказывается, что каждый автоматный язык задается некоторым детерминированным конечным автоматом. 2.1. Недетерминированные конечные автоматы
Определение
2.1.1.
Конечный
автомат
(finite automaton, finite-state machine) - это пятерка
Пример
2.1.2.
Пусть Q
= {1,2},
Тогда
Замечание 2.1.3. Конечные автоматы можно изображать в виде диаграмм состояний (state diagram) (иногда их называют диаграммами переходов (transition diagram)). На диаграмме каждое состояние обозначается кружком, а переход - стрелкой. Стрелка из p в q, помеченная словом x, показывает, что является переходом данного конечного автомата. Каждое начальное состояние распознается по ведущей в него короткой стрелке. Каждое допускающее состояние отмечается на диаграмме двойным кружком. Пример 2.1.4. На диаграмме изображен конечный автомат из примера 2.1.2.
Замечание 2.1.5. Если в конечном автомате имеются несколько переходов с общим началом и общим концом, то такие переходы называются параллельными. Иногда на диаграмме состояний конечного автомата параллельные переходы изображают одной стрелкой. При этом метки переходов перечисляют через запятую. Пример 2.1.6. На диаграмме снова изображен конечный автомат из примера 2.1.2.
Определение
2.1.7.
Путь
(path) конечного автомата - это кортеж
Замечание
2.1.8.
Для любого состояния
Определение 2.1.9. Путь называется успешным если его начало принадлежит I, а конец принадлежит F.
Пример
2.1.10.
Рассмотрим конечный автомат из примера
2.1.2. Путь
Определение 2.1.11. Слово w допускается (is accepted, is recognized) конечным автоматом M, если оно является меткой некоторого успешного пути. Определение 2.1.12. Язык, распознаваемый конечным автоматом M, - это язык L(M), состоящий из меток всех успешных путей (то есть из всех допускаемых данным автоматом слов). Будем также говорить, что автомат M распознает (recognizes, accepts) язык L(M).
Замечание
2.1.13.
Если
Пример 2.1.14. Пусть , где Q = {1,2}, , I = {1}, F = {1,2},
Тогда
Определение 2.1.15. Два конечных автомата эквивалентны, если они распознают один и тот же язык. Определение 2.1.16. Язык L называется автоматным (finite-state language), если существует конечный автомат, распознающий этот язык. Замечание 2.1.17. Обычно в учебниках используется более узкое определение недетерминированного конечного автомата, но это не меняет класса автоматных языков (см. лемму 2.3.3.).
Пример
2.1.18.
Рассмотрим однобуквенный алфавит
Замечание 2.1.19. Каждый конечный язык является автоматным. Определение 2.1.20. Состояние q достижимо (reachable) из состояния p, если существует путь, началом которого является p, а концом - q. Лемма 2.1.21. Каждый автоматный язык распознается некоторым конечным автоматом, в котором каждое состояние достижимо из некоторого начального состояния и из каждого состояния достижимо хотя бы одно заключительное состояние.
Пример
2.1.22.
Рассмотрим конечный автомат
,
где Q
= {1,2,3,4},
Удалим
те состояния (и содержащие их переходы),
которые не удовлетворяют требованиям
леммы 2.1.21. Получается эквивалентный
конечный автомат
Замечание 2.1.23 Естественным обобщением конечного автомата является конечный преобразователь (finite-state transducer), позволяющий на каждом такте отправить несколько символов в дополнительный "выходной" поток. В некоторых книгах конечными автоматами называют именно такие устройства (с выходным потоком). В данном пособии конечные преобразователи рассматриваться не будут.
Упражнение
2.1.24.
Найти конечный автомат, распознающий
язык
Упражнение
2.1.25.
Найти конечный автомат, распознающий
язык
Упражнение
2.1.26.
Найти конечный автомат, распознающий
язык
Упражнение
2.1.27.
Найти конечный автомат, распознающий
язык
Упражнение
2.1.28.
Найти конечный автомат, распознающий
язык
Упражнение
2.1.28.
Найти конечный автомат, распознающий
язык
|
|
|
,
где
-
конечный входной
алфавит
(или просто алфавит)
данного конечного автомата, Q
и
-
конечные множества,
,
.
Элементы Q
называются состояниями
(state), элементы I
- начальными
(initial) состояниями, элементы F
- заключительными
или допускающими
(final, accepting) состояниями. Если
,
то
называется
переходом
(transition) из p
в q,
а слово x
- меткой
(label) этого перехода.
,
I
= {1},
F
= {2},
-
конечный автомат.
,
где
и
для
каждого i.
При этом q0
- начало
пути
qn
- конец
пути
n
- длина
пути
w1...wn
- метка
пути.
существует
путь
.
Его метка -
,
начало и конец совпадают.
является
успешным. Его метка - baaab.
Длина этого пути - 4.
,
то язык, распознаваемый конечным
автоматом
,
содержит
.
.
При любых фиксированных
и
язык
является
автоматным.
,
I
= {1,2,4},
F
= {1,3,4},
,
где Q'
= {1,4},
I'
= {1,4},
F'
= {1,4},
,
где
,
и
для
любого
2.2. Конфигурация конечного автомата
Определение
2.2.1.
Конфигурацией
или мгновенным
описанием
(instantaneous description) конечного автомата
называется
любая упорядоченная пара
Замечание 2.2.2. Содержательно конфигурация представляет собой "мгновенное описание" конечного автомата. Если представить, что исходное слово, принадлежность которого рассматриваемому языку надо проверить, дано в некотором "входном потоке", то в конфигурации слово w есть та часть исходного слова, которая пока осталась во входном потоке (это некоторый суффикс исходного слова), а q - текущее состояние "управляющего устройства".
Определение
2.2.3.
Определим на множестве всех конфигураций
конечного автомата M
бинарное отношение
Пример 2.2.4. Рассмотрим конечный автомат
из
примера 2.1.2. Тогда
Определение
2.2.5.
Бинарное отношение
Пример
2.2.6.
Для конечного автомата из примера
2.1.2 выполняется
Лемма
2.2.7.
Пусть
дан конечный автомат
.
Слово
принадлежит
языку L(M)
тогда и только тогда, когда для некоторых
Лемма
2.2.8.
Если
Доказательство.
Лемму легко доказать индукцией по
количеству тактов в вычислительном
процессе, ведущем из конфигурации
Упражнение 2.2.9. Рассмотрим конечный автомат.
Перечислить
все конфигурации
,
удовлетворяющие условию
Упражнение
2.2.10.
Существуют ли конечный автомат M,
состояния q1,
q2
и слова x,
y,
z,
такие что
Упражнение
2.2.11.
Как связаны |Q|,
2.3. Конечные автоматы с однобуквенными переходами Лемма 2.3.1. Каждый автоматный язык распознается некоторым конечным автоматом, не содержащим переходов с метками длины больше единицы и имеющим ровно одно начальное состояние и ровно одно заключительное состояние. Пример 2.3.2. Рассмотрим язык, заданный конечным автоматом , где Q = {1,2}, , I = {1,2}, F = {1,2},
Тот же язык распознается конечным автоматом , где Q' = {0,1,2,3,4,5}, I' = {0}, F' = {5},
Здесь
первые два перехода заменяют старый
переход
Лемма 2.3.3. Каждый автоматный язык распознается некоторым конечным автоматом, содержащим только переходы с метками длины единица и имеющим ровно одно начальное состояние. Доказательство. Согласно лемме 2.3.1 можно предположить, что исходный язык задан конечным автоматом , не содержащим переходов с метками длины больше единицы, причем |I| = 1. Построим искомый конечный автомат , положив Q' = Q, I' = I,
Пример 2.3.4. Пусть , где Q = {1,2,3}, , I = {1}, F = {3},
Легко
убедиться, что
Упражнение
2.3.5.
Найти конечный автомат с однобуквенными
переходами, распознающий язык
Упражнение
2.3.6.
Найти конечный автомат с однобуквенными
переходами, распознающий язык
Упражнение 2.3.7. Существуют ли автоматный язык, который не распознается никаким конечным автоматом, содержащим только переходы с метками длины единица и имеющим ровно одно начальное состояние и ровно одно заключительное состояние?
|
|
|
|
|
,
где
и
.
(такт
работы
(step)) следующим образом. Если
и
,
то
.
Иногда вместо
пишут
.
.
определяется
как рефлексивное, транзитивное
замыкание отношения
.
и
.
и
верно
.
и
,
то
.
в
конфигурацию
.
.
и
?
,
,
|w|
и число достижимых из
(в
смысле
)
конфигураций?
и
следующие два перехода заменяют старый
переход
.
Чтобы обеспечить единственность
начального состояния, добавлены
переходы
и
.
Последние два перехода в
обеспечивают
единственность заключительного
состояния.
.
Тот же язык распознается конечным
автоматом
,
где F'
= {2,3}
и
2.4. Характеризация праволинейных языков
Теорема 2.4.1. Каждый автоматный язык является праволинейным.
Без
ограничения общности можно предположить,
что исходный язык задан конечным
автоматом
,
где
и
I
= {q0}.
Положим N
= Q,
S
= q0
и
Пример 2.4.2. Язык, распознаваемый конечным автоматом из примера 2.1.2, порождается грамматикой
Теорема 2.4.3. Каждый праволинейный язык является автоматным.
Доказательство.
Без ограничения общности можно
предположить, что исходный язык задан
праволинейной грамматикой, не содержащей
правил вида
,
где
.
Положим Q
= N,
I
= {S},
и
.
Пример 2.4.4. Пусть . Рассмотрим грамматику
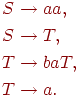
Она эквивалентна грамматике
Язык, порождаемый этими грамматиками, распознается конечным автоматом , где Q = {S,T,E}, I = {S}, F = {E} и
Упражнение
2.4.5.
Найти праволинейную грамматику,
порождающую язык
Упражнение 2.4.6. Существует ли такая праволинейная грамматика G, что язык L(G)R не порождается ни одной праволинейной грамматикой, имеющей столько же правил, сколько грамматика G?
Упражнение 2.4.7. Существует ли такая праволинейная грамматика G, что язык L(G)R не порождается ни одной праволинейной грамматикой с количеством правил n + 1, где n - количество правил в грамматике G?
Упражнение 2.4.8. Существует ли такая праволинейная грамматика G с тремя вспомогательными символами, что язык L(G)R не порождается ни одной праволинейной грамматикой с тремя вспомогательными символами?
2.5.Нормальная форма праволинейных грамматик
Определение
2.5.1.
Праволинейная
грамматика в нормальной форме
(автоматная
грамматика, регулярная грамматика,
finite-state grammar) - это праволинейная грамматика,
в которой каждое правило имеет вид
,
,
или
,
где
,
,
.
Теорема 2.5.2. Каждая праволинейная грамматика эквивалентна некоторой праволинейной грамматике в нормальной форме.
Доказательство. Применим последовательно теорему 2.4.3, лемму 2.3.3 и воспользуемся конструкцией из доказательства теоремы 2.4.1.
Теорема 2.5.3. Если праволинейный язык не содержит пустого слова, то он порождается некоторой праволинейной грамматикой в нормальной форме без -правил.
Упражнение 2.5.4. Найти праволинейную грамматику, эквивалентную грамматике
Упражнение 2.5.5. Найти праволинейную грамматику в нормальной форме без -правил, порождающую язык
Упражнение 2.5.6. Найти праволинейную грамматику в нормальной форме без -правил, порождающую язык
2.6. Детерминированные конечные автоматы
Определение 2.6.1. Конечный автомат называется детерминированным (deterministic), если
множество I содержит ровно один элемент;
для каждого перехода выполняется равенство |x| = 1;
для любого символа и для любого состояния
существует
не более одного состояния
со
свойством
.
Пример 2.6.2. Конечный автомат из примера 2.1.14 является детерминированным.
Определение 2.6.3. Детерминированный конечный автомат называется полным (complete), если для каждого состояния и для каждого символа найдется такое состояние , что .
Пример 2.6.4. Конечный автомат из примера 2.1.14 эквивалентен полному детерминированному конечному автомату , где Q = {1,2,3}, , I = {1}, F = {1,2},
Замечание
2.6.5.
Некоторые авторы используют в определении
полного детерминированного конечного
автомата вместо отношения
функцию
.
От функции
можно
перейти к отношению
,
положив
Упражнение 2.6.6. Является ли детерминированным следующий конечный автомат?
Упражнение
2.6.7.
Является ли полным следующий
детерминированный конечный автомат с
алфавитом
?
