ФГБОУ ВПО

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра математики

Реферат

на тему:

«Приближение функций по методу наименьших квадратов. (Основные понятия дифференциальной геометрии. Кривизна, радиус кривизны. Формулы Френе. Уравнения касательной к кривой, касательной плоскости и нормали к поверхности)».

Выполнил: ст.гр. ПБ-10-01 Хмелевский А.С.

Проверил: доцент Абзалимов Р.Р.

Уфа 2011

Содержание

1. Кривизна, радиус кривизны.

2. Формулы Френе.

3. Уравнения касательной к кривой, касательной плоскости и нормали к поверхности.

4. Приближение функций по методу наименьших квадратов.

5. Примеры для решения

6. Задачи

Кривизна, радиус кривизны

При движении вдоль кривой её касательная меняет направление. Скорость этого вращения (отношение угла поворота касательной за бесконечно малый промежуток времени к этому промежутку) при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. Производная же по времени положительного единичного вектора касательной называется в этом случае вектором кривизны кривой. То и другое - функции точки кривой. Кривизна есть абсолютная величина вектора кривизны.

В случае произвольного параметрического задания кривой кривизна кривой в трехмерном пространстве определяется по формуле

где r(t)- вектор-функция с координатами x(t), y(t), z(t).

В координатах:

Для кривой в более многомерном пространстве можно заменитьвекторное произведение, обозначенное здесь квадратными скобками, на внешнее произведение.

Также для кривой в любой размерности пространства можно воспользоваться формулой вектора кривизны:

и фактом, что кривизна есть его модуль, а также выражением для единичного вектора касательной

и

и получить для кривизны формулу:

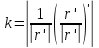
или, раскрыв скобки:

Прямые и только прямые имеют всюду равную нулю кривизну. Поэтому кривизна наглядно показывает, насколько (в данной точке) кривая отличается от прямой линии: чем ближе кривизна к нулю, тем это отличие меньше. Кривизна окружности радиуса R равна 1/R.

Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость.

Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями 

x=x(t), y=y(t) , определяется по формуле

Знак + или − берётся по соглашению, но сохраняется вдоль всей кривой.

Формулы Френе

Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником. Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей.

Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой:

где  и  — кривизна и кручение кривой в указанной точке.

Единичные векторы , соответственно для касательной, главной нормали и бинормали кривой, при движении вдоль кривой изменяются. При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы:

(2) где дифференцирование идёт по дуге кривой. Формулы (2) называют формулами Френе́, или Френе-Серре.

Кинематическое истолкование

Будем рассматривать длину дуги заданной кривой как время, а трёхгранник Френе — как твёрдое тело, движущееся вдоль кривой. Тогда это движение в каждый момент времени состоит из поступательного (вдоль касательной) и мгновенного вращения сугловой скоростью (вектор Дарбу). Из формул Френе вытекает:

Это означает, что вектор мгновенного вращения лежит в спрямляющей плоскости и распадается на 2 составляющие: вращение вокруг би нормали со скоростью  (поворот) и вращение вокруг касательной со скоростью  (кручение).

Уравнения касательной к кривой, касательной плоскости и нормали к поверхности

Если в качестве M взять кривую, а в качестве m прямую, проходящую через точку O кривой, то при  условие соприкосновения определяет касательную к кривой в точке O (рис. 1). Касательная в точке P кривой также может быть определена как предельное положение секущей, проходящей через P и близкую к ней точку P1, когда P1 стремится к P.

Гладкая регулярная кривая в каждой точке имеет определённую касательную. Направление касательной в точке  кривой, задаваемой уравнениями (1), совпадает с направлением вектора . В векторной записи это производная .

В точке кривой построены векторы касательной (T), главной нормали (N) и бинормали (B). Показана также соприкасающаяся плоскость, содержащая касательную и главную нормаль.

В дифференциальной геометрии выводятся уравнения касательной для различных способов аналитического задания кривой. В частности, для кривой, задаваемой уравнениями (1), уравнения касательной в точке, отвечающей значению параметра t0, будут

,где индекс  указывает на значение функций  и их производных в точке 

Для плоской кривой уравнение касательной в точке . имеет следующий вид.

Параметрическое задание: 

Явное задание: 

Неявное задание: 

Если взять в качестве m плоскость, проходящую через точку O кривой M, то условие соприкосновения при  определяет соприкасающуюся плоскость кривой (рис. 1). Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.

Пусть  — уравнение кривой. Тогда уравнение   её соприкасающейся плоскости определяется из соотношения:

В координатах оно имеет вид:

Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Также нормалью и бинормалью для краткости могут называть единичные векторы вдоль этих прямых (при этом направление вектора главной нормали обычно выбирают совпадающим с направлением вектора кривизны кривой).

Векторное уравнение бинормали в точке, отвечающей значению  параметра t, имеет вид:

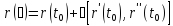
Направление главной нормали может быть получено как двойное векторное произведение:

Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке имеет следующий вид.

Параметрическое задание: 

Явное задание: 

Неявное задание: 

Приближение функций по методу наименьших квадратов.

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Пусть в результате некоторого эксперимента получены данные в виде чи-

сел записанных в таблицу

x			……
y			……

На основании этих данных требуется установить функциональную зави­симость величины y от величины x: y = f( x). Вид функции y = f( x) уста­навливается обычно или из теоретических соображений или визуально, иссле­дуя расположение точек (x1,y1), (x2,y2 ),..., (xn,yn ) на плоскости XOY.

Наиболее часто в качестве подбираемой функции используют следующие функции:

Наиболее часто в качестве подбираемой функции используют следующие функции:

а) полином: f (x) = a₀ + a₁x + a₂x² + a₃x³ +...+a_mx^m = P_m (x);

б) дробно-рациональную

в) экспоненциальную: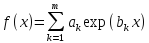

г) логарифмическую и другие функции,

где , ……,, числа, заранее неизвестные. И задача заключается именно в нахождении этих чисел

Замечание:

1. Если нет никаких теоретических указаний о виде зависимости

y = f(x), то следует искать наиболее простую формулу, содержащую как можно меньшее количество параметров , ;

2. Полное совпадение с данными эксперимента и не желательно, т.к. определяемая функция будет повторять ошибки экспериментатора.

Существует много различных методов нахождения коэффициентов

, ……,,.Они излагаются в учебниках по численным методамnматематики, там же излагаются их достоинства и недостатки. Здесь будет рассмотрен один из этих методов - метод наименьших квадратов.

Итак, имеем y = f(, ……), функцию многих переменных, которая зависит от x и еще нескольких неизвестных величин , ……

Составим новую функцию

Величины надо найти таким образом, чтобы функция

Φ= Φ() имела наименьшее значение. Иными словами, отклонение экспериментальных точек от теоретической кривой должно быть минимальным.

Применяем необходимое условие экстремума функции нескольких переменных:

В результате получится система из (m+ 1) линейного уравнения с

(m+ 1) − м неизвестными . В каждом конкретном случае иссле-

дуется вопрос о существовании решения этой системы, единственности этого

решения и о наличии минимума функции Φ =Ф(, при полученных значениях величин .

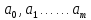Рассмотрим частные случаи подбираемой функции y = f(x).

1. Пусть y = f(x) − полином 1-й степени, т.е.

y = f(x, , ) = + x. График этой функции есть прямая линия. В этом

случае вспомогательная функция Φ = Φ( ), есть функция двух перемен-

ных и имеет вид:

Тогда система будет представлена следующими двумя уравнениями:

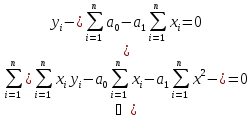
Теперь необходимо вычислить коэффициенты системы (значения yi и xi

даны в таблице. Обозначим

Тогда система принимает вид:

Эта система из двух линейных уравнений с двумя неизвестными и .

Решим систему по формулам Крамера

Если Δ ≠ 0, то решение существует и оно единственно и это решение:

При найденных значениях и функция имеет минимальное значение.