8.22. Что такое с-ядро коалиционной игры?

Коалиционная игра является стратегически эквивалентной игре если

.

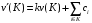Игра с характеристической функцией имеет (0,1) – редуцированную форму, если выполняется следующее соотношение

Пусть в коалиционной игре 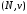имеется два дележа и 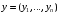, – некоторая коалиция. Тогда дележ доминирует по коалиции 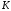над дележом 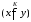, если

1) ,

2) 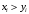для любого .

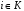Множество дележей, которые в любых коалициях не доминируется никакими другими дележами, называют С- ядром этой игры.

Теорема 8.5.2. Для того, чтобы дележ принадлежал С-ядру коалиционной игры с характеристической функцией необходимо и достаточно, чтобы выполнялось неравенство

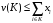для всех непустых .

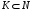Теорема утверждает, что дележ входит в C-ядро тогда и только тогда, когда он удовлетворяет минимальным требованиям каждой коалиции. В игре с пустым С-ядром всегда найдется одна неполностью удовлетворенная коалиция.

8.23. Дать определение вектора Шепли.

Пусть - игра игроков в форме характеристической функции.

Решением игры будем называть дележ , называемый вектором цен Шепли, удовлетворяющий следующим аксиомам.

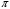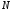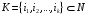
Аксиома 1. Если - характеристическая функция на множестве игроков , - перестановка элементов множества такая, что для каждой коалиции , то для всех

.

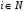
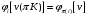Таким образом, всем игрокам приписываются равные цены (независимо от их номеров).

Аксиома 2. .

Таким образом, вектор 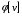является дележом.

Аксиома 3.Если 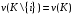для всех 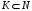, то 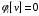. Таким образом, если игрок 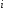ничего не добавляет к любой коалиции, то его цена равна 0.

Аксиома 4.Есл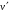и и 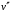- характеристические функции на множестве игроков , то

для всех .

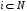Таким образом, если одна игра не влияет на реализацию второй, то выигрыши игроков в отдельных играх должны складываться.

8.24. Как построить вектор цен Шепли во взвешенных мажоритарных играх?

Теорема Шепли. Для всех характеристических функций существует единственный дележ , удовлетворяющий аксиомам 1 - 4, с координатами

,

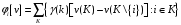где 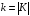и .

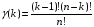В определенном смысле величину 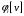можно рассматривать как меру “силы” 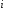-го игрока. Особенно ярко это проявляется в так называемых взвешенных мажоритарных играх, которые возникают при различных голосованиях. Игрок 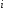имеет 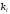голосов. Коалиция “побеждает”, если сумма ее голосов не меньше некоторой доли от их общего количества. Тогда величина всегда равна 0 или 1, причем принимает значение 1 в том и только в том случае, если 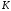- выигрывающая коалиция, а - проигрывающая. Поэтому получаем, что для всех

,

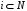
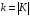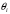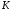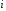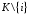где и суммирование осуществляется по множеству всех выигрывающих коалиций , содержащих , и таких, что - не выигрывающая коалиция.