Введение

Применение современных пакетов, систем и технологий, например, ERP, e-CRM, SCM, XML и других, не снимает полностью неопределенность для лица, принимающего окончательное решение, от которого может зависеть успех фирмы или проекта. Для снижения вероятности ошибок при оперативном решении ответственных задач предлагается итерационный алгоритм, представляющий собой комбинацию метода экспертных оценок и байесовского подхода [1, 2].

1.Основные положения байесовского подхода

Во многих задачах принятия решений априорная вероят­ностная информация о состояниях природы может быть из­менена после получения новых экспертных оценок или в ре­зультате наблюдения соответствующих событий, связанных с состояниями и подтверждающих или опровергающих априор­ную информацию.

Как отмечается в справочнике [3], многие статистические задачи независимо от методов их решения обладают общим свойством: до того как получен конкретный набор данных, в качестве потенциально приемлемых для изучаемой ситуации рассматривается несколько вероятностных моделей. После то­го как получены данные, возникает выраженное в некотором виде знание об относительной приемлемости этих моделей. Од­ним из способов "пересмотра" относительной приемлемости ве­роятностных моделей является байесовский подход, основой ко­торого выступает известная теорема Байеса.

Несмотря на то что так называемая традиционная частот­ная школа статистического вывода, представленная работами таких ученых, как Фишер, Ньюмен, Пирсон, и многими други­ми, доминирует в статистике в настоящее время, байесовские методы показали чрезвычайно стремительное развитие в по­следние десятилетия. Причина этого заключается в том, что байесовский подход имеет ряд существенных преимуществ, ко­торые делают его достаточно привлекательным для широкого применения [2].

Основное отличие байесовского подхода от других стати­стических подходов состоит в том, что до того, как будут по­лучены данные, лицо, принимающее решение, или статистик рассматривает степени своего доверия к возможным моделям и представляет их в виде вероятностей. Как только данные по­лучены, теорема Байеса позволяет рассчитать новое множество вероятностей, которые представляют пересмотренные степени доверия к возможным моделям, учитывающие новую инфор­мацию, поступившую благодаря данным.

Статистические данные зачастую отсутствуют в реальных задачах анализа риска и принятия решений, что делает ис­пользование многих традиционных частотных подходов непра­вомерным [1]. Имеющаяся в распоряжении информация может содержать только субъективные оценки в виде экспертных оце­нок и суждений. Более того, ситуация, в которой принимается решение, может быть вообще новой и никогда ранее не анали­зируемой. Эти особенности усложняют процесс принятия ре­шений и могут поставить под сомнение какие-либо выводы и заключения. Поэтому в такой ситуации байесовский подход мо­жет оказаться весьма полезным и эффективным.

2.Байесовский подход

Пусть требуется из множества V ={и₁, и₂, ..., u_n} вариантов решений, показатели эффективности которых примерно

одинаковы, выбрать наиболее целесообразный и* для реализации.

Обработка результатов работы "узкой" группы экспертов показала, что их мнения не могут быть признаны согласованными (коэффициент конкордации низок) и среди рассматриваемых вариантов нет выделяющегося "лидера".

Идея алгоритма заключается в последовательном привлечении дополнительных экспертов и подсчета для каждого проекта и е V средней апостериорной вероятности того, что этот проект является оптимальным. Работа продолжается до тех пор, пока средняя апостериорная вероятность одного из проектов u_a множества V не будет существенно выше, чем для альтернативных проектов. При соблюдении некоторых условий на возможные исходы последующих экспертиз данный проект u_a считается оптимальным.

Результат работы каждого дополнительно привлекаемого эксперта рассматривается как исход проведенного опыта, и расчет апостериорной вероятности производится по формуле Байеса, т.е.

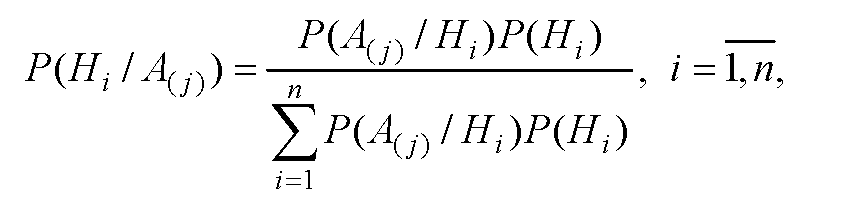
где Hi – предположение (гипотеза) о том, что вариант υi является оптимальным; A( j) – результат экспертизы (событие) об

оптимальности варианта υ j ; n – число рассматриваемых вариантов (мощность множества V ); P(Hi ),P(Hi / A( j) ) –

априорная и апостериорная вероятности гипотезы Hi , соответственно; P(A( j) / Hi ) – вероятность события A( j) , если имеет

место гипотеза Hi (правдоподобие).

Будем полагать, что событие A( j ) произошло, если вариант υ j очередной эксперт расположил на 1-е место при

n = 2…3, и на 1-е или 2-е место при n > 3 .

Если произошло событие A( j) , то апостериорная вероятность P(Hi / A( j) ) рассчитывается по формуле:

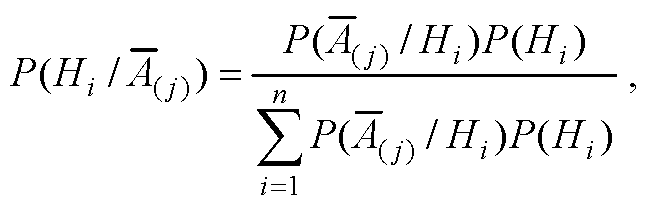
где P(Hi / A( j) ) – апостериорная вероятность гипотезы Hi при событии A( j) .

По результатам работы очередного k-го эксперта рассчитываются усредненные апостериорные вероятности по формуле

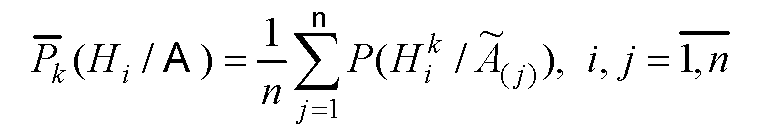
где ~A j – событие, связанное с проверкой гипотезы H_i ^j , т.е. того, что

k-й эксперт вариант υ j поставит на первые места, для части слагаемых суммы имеет место A( j) , для другой – A( j) .

Вероятности P(Hi ), P(Hi / A( j) ), P(Hi / A( j) ), Pk (Hi / A ) естественно удовлетворяют условию полноты группы событий, т.е.

и P(A( j) / Hi )+ P(A( j) / Hi )= 1, i, j = 1, n.

В качестве оптимального варианта υ после k-й экспертизы берется тот, для которого вероятность, рассчитанная по формуле, максимальна и выполняется условие, что некоторое наперед заданное число m последующих экспертиз не изменяет соотношения

где H(υ^* ) – гипотеза об оптимальности варианта υ^* , H(υi ) = Hi .

При использовании байесовского подхода для решения подобных задач важную роль играет формализация правила "остановки" в процессе проведения экспертиз. С одной стороны, своевременное прекращение итераций экономит средства, затрачиваемые на проведение экспертиз. С другой стороны, необходима уверенность, что дальнейшее привлечение

экспертов не приведет к кардинальному изменению усредненной апостериорной вероятности и принятию другого варианта для реализации.

Наиболее естественно решение об "остановке" принимать по двум показателям: числе m дополнительных экспертов, высказывания которых могут изменить выбор оптимального варианта, и вероятности Pm того, что результаты высказываний этих экспертов приведут к изменению варианта, т.е. гипотезы, для которой усредненная апостериорная вероятность максимальна.

Определение показателей m и Pm произведем при следующих допущениях:

1) в множестве V можно выделить два лидирующих варианта υa и υb ;

2) проведена обработка мнений k экспертов, при этом варианту υa отдавалось предпочтение (исход A ) ka раз (kа ≤ k) и

варианту υb (исход В ) – kb раз ( ) kb < ka , т.е. по результатам k итераций вариант ka считается предпочтительным (вероятность Pk (H(υa ) / A ) – максимальна);

3) в качестве вероятностей исходов A и B принимаются оценки

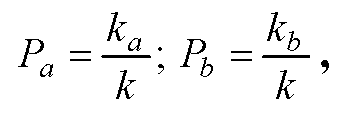
причем вероятность Pa > 0,5 ;

4) исходы A и B при последующих высказываниях экспертов являются независимыми и совместимыми;

5) очередность исходов в m экспертизах не влияет на конечный результат.

При данных допущениях имеет место следующая лемма.

Лемма 1. Если

то соотношение

становится возможным при

Доказательство леммы непосредственно следует из формулы Байеса и принятых допущений.

Для определения вероятности Pm (b) , характеризующей возможность неравенства, используем комбинацию моделей Бернулли для повторяющихся испытаний.

Лемма 2. Если имеет место Pk (H (υa ) А ) > Pk (H (υb ) А ) , kа > kb, и m ≥ 2 , то вероятность выполнения неравенства при минимальном значении m определяется формулой

Равенство означает, что все m привлекаемых дополнительно экспертов выскажутся отрицательно относительно варианта υa (исходы A ) и положительно относительно υb (исходы B ). Формула непосредственно следует из распределения вероятностей возможных сложных событий при m испытаниях, в которых события A и B могут принимать по два исхода с разными вероятностями. Такое распределение при использовании моделей Бернулли для событий A и B имеет следующий вид:

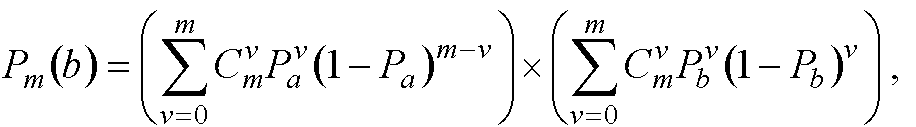
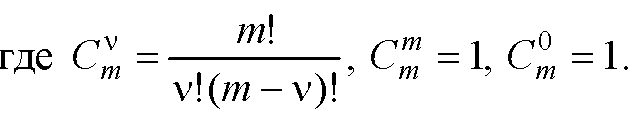
Следует заметить, что вероятности Pa , Pb необходимо корректировать после каждой итерации.