47. Квантовая механика. Волновая ф-я и её физический смысл.Уравнение Шредингера. Диалектическое единствокорпускулярных и волновых свойств частиц.

КВАНТОВАЯ МЕХАНИКА , изучает состояния микрочастиц и их систем (элементарных частиц, атомных ядер, атомов, молекул, кристаллов), изменение этих состояний во времени, а также связь величин, характеризующих состояния микрочастиц, с эксперим. макроскопич. величинами. К. м. исследует уровни энергии, пространственные и импульсные характеристики систем частиц, эволюцию этих систем во времени, вероятности переходов между состояниями под влиянием взаимод. между системами и внеш. воздействий. В нерелятивистской К.м. для средних скоростей v всех частиц системы предполагается выполненным условие: (v/с)²<<1, где с - скорость света. Результаты нерелятивистской К. м. переходят в таковые классич. механики, когда выполняется принцип соответствия, т.е. когда произведение импульса каждой из взаимодействующих частиц на размер области, в к-рой это взаимод. существенно меняется, велико по сравнению с постоянной Планка =1,0546^.10^-34 Дж^.с. К.м. была сформулирована для объяснения явлений, к-рые не могли быть объяснены в рамках классич. механики и электродинамики. Трудами М. Планка (1900), А. Эйнштейна (1905, 1916) и Н. Бора (1912) было показано, что атомы имеют стационарные состояния, переходы между к-рыми происходят при излучении или поглощении кванта света, имеющего энергию и импульс , где  и k - круговая частота и волновой вектор световой волны соответственно. Проблема объяснения этих св-в атомов была решена почти одновременно с неск. сторон. Л. де Бройль (1924) предложил распространить волновые представления, привычные для описания электромагн. поля, на атомные частицы, сопоставляя своб. движению частицы с энергией Е и импульсом р волну распространяющуюся в пространстве и времени t (r-радиус-вектор частицы, i - мнимая единица, С - постоянный множитель). Тем самым он предсказал дифракцию таких частиц при рассеянии на кристаллах. В. Гейзенберг (1925) нашел матричное представление для динамич. переменных классич. механики, позволившее объяснить структуру уровней энергии нек-рых систем. Так возникла матричная механика. Э. Шрёдингер [Шредингер] (1926) предложил дифференц. ур-ние, решениями к-рого при заданных граничных условиях являются собств. ф-ции , названные волновыми ф-циями, и собств. значения, указывающие уровни энергии системы. Так возникла волновая механика. Анализ показал, что подходы В. Гейзенберга и Э. Шрёдингера [Шредингера] эквивалентны, поэтому термины "матричная механика", "волновая механика" и наиб. употребительный сейчас "К. м." являются синонимами. С вычислит, точки зрения, как правило, наиб. удобным оказывается метод решения ур-ния Шрёдингера [Шредингера]. Осн. постулаты К.м. При рассмотрении задач о состояниях частиц и их систем осн. положения К.м. обычно формулируют в след, виде: 1. Состояние системы из N микрочастиц полностью определяется волновой ф-цией (r₁,...,r_N), где r_l,..., r_N - радиусы-векторы частиц. Если - элемент объема в конфигурац. пространстве переменных N частиц, то величина |(r₁,...,r_N; t)|²d пропорциональна вероятности найти в момент времени t первую частицу вблизи точки с радиусом-вектором r₁ в объеме dr₁ (т. е. в параллелепипеде со сторонами dx₁, dy₁ и dz₁, одной из вершин к-рого служит точка r₁), вторую частицу - вблизи точки r₂ в объеме dr₂ и т.д. (М. Борн, 1926). 2. Каждой наблюдаемой физ. величине А (координате, импульсу, энергии и т.п.) сопоставляется линейный оператор . Для системы, находящейся в состоянии с волновой ф-цией , при измерении величины А м.б. получены лишь те значения а_i, к-рые являются собств. значениями оператора , т. е. удовлетворяют равенству: , где _i нек-рая ф-ция от тех же переменных, что и волновая ф-ция системы. Вероятность найти значение а_i определяется квадратом модуля интеграла , а среднее значение - интегралом , где ^_i и ^* - ф-ции, комплексно сопряженные _i и . Поскольку величины а_i и их среднее вещественны, на операторы накладывается дополнит. ограничение: они должны быть эрмитовыми. Это означает, что для любых ф-ций  и  должно выполняться соотношение: 3. Операторы , отвечающие наблюдаемым физ. величинам, к-рые определены в классич. механике (энергия, импульс и т. п.), получаются, если в соотношениях, установленных для этих величин классич. физикой, заменить координаты частиц операцией умножения на эти координаты, а импульсы - операцией дифференцирования (с точностью до множителя) по соответствующей переменной (т. наз. сопряженной координате). Напр., вместо координаты х употребляют оператор : ; вместо компоненты импульса р_х - оператор : Полученный при такой замене оператор соответствующей физ. величины должен быть записан так, чтобы он был эрмитовым. Так, операторы проекций момента кол-ва движения частицы записываются след. образом: , и . Собств. значения оператора , равные , определяются неотрицат. целыми числами l, а собств. значения оператора проекции момента на к.-л. фиксированное направление, напр. ось z, - числами -l , -l+1,...,+l. 4. Волновые ф-ции , описывающие состояния системы, являются решениями ур-ния Шрёдингера [Шредингера], или волнового ур-ния: где -оператор полной энергии системы, наз. оператором Гамильтона или гамильтонианом; он получается из классич. ф-ции Гамильтона по правилам, указанным в п. 3. 5. У каждой элементарной частицы м.б. собств. момент кол-ва движения, не связанный с перемещением ее как целого. Этот момент наз. спином или собств. моментом кол-ва движения. Спин измеряется в единицах постоянной Планка и равен , где s - характерное для каждого вида частиц целое или полуцелое неотрицат. число, наз. спиновым квантовым числом или просто спином . Проекция спина на любое фиксир. направление в пространстве может принимать значения (в единицах ) — s, —s+1,...,+s. Напр., спин электрона, протона и нейтрона равен ¹/₂, спин -мезона-0, спин ядра атома дейтерия - l. Т. обр., частица или система из неск. частиц может находиться в разл. квантовых состояниях, каждому из к-рых отвечает свое значение спина и его проекции. Это обстоятельство обычно отражается в том, что для каждой частицы вводится помимо трех пространств, переменных дополнит, четвертая переменная , от к-рой зависят и спиновые операторы. Волновая ф-ция системы с учетом спина м. б. записана в виде: (r₁, _i; r₂, ₂;...; r_N; _N; t)=(1,2, ...,N; t). Системы тождеств, частиц (одной и той же массы, заряда и т.д.) с целочисленным спином подчиняются статистике Бозе - Эйнштейна, системы частиц с полуцелым спином -статистике Ферми-Дирака (см. Статистическая термодинамика ). В свою очередь, симметрия волновой ф-ции системы тождеств. частиц полностью определяется типом статистики, к-рой подчиняются частицы: для частиц с целым спином волновая ф-ция симметрична, т.е. не меняется при перестановке индексов двух тождеств. частиц; для частиц с полуцелым спином волновая ф-ция антисимметрична, т.е. меняет знак при любой такой перестановке (В. Паули, 1940). Перестановка индексов частиц означает переход к описанию того же состояния системы при др. порядке нумерации частиц. Состояния квантовой системы, описываемые волновыми ф-циями, наз. чистыми состояниями. Для них имеется максимально полная информация о квантовой системе. Однако в К. м. возможно описание и таких состояний, с к-рыми нельзя сопоставить определенную волновую ф-цию, а можно только указать набор вероятностей |с_i|² появления при измерении к.-л. физ. величины А состояний, в к-рых эта величина принимает определенные значения. Для таких состояний нельзя построить волновую ф-цию в виде линейной комбинации волновых ф-ций _i чистых состояний с коэффициентами с_i, поскольку известны лишь квадраты модуля этих коэффициентов, но неизвестны их фазы. Такие состояния наз. смешанными. Они м.б. охарактеризованы нек-рой операторной ф-цией, наз. матрицей плотности и позволяющей вычислять средние значения и вероятности разл. значений физ. величин в таком состоянии. Матрица плотности  зависит от тех переменных, к-рые определяют квантовую систему, и от времени; она удовлетворяет квантовому ур-нию Лиувилля: Ур-ние Шрёдингера [Шредингера] и мат. аппарат К. м. Ур-ние Шрёдингера [Шредингера] является линейным дифференциальным и - что очень важно - однородным ур-нием. Это означает, что если ₁ и ₂ - к.-л. два решения этого ур-ния, то и любая их линейная комбинация c₁_+с₂₂ с постоянными коэф. c₁ и с₂ будет также решением ур-ния Шрёдингера [Шредингера] (т. наз. принцип суперпозиции). Если гамильтониан не зависит в явном виде от времени (напр., для своб. молекулы или для молекулы, находящейся во внеш. стационарном поле), ур-ние Шрёдингера [Шредингера] допускает разделение пространственных переменных, определяющих положения частиц, и времени. Волновая ф-ция состояния с энергией E_k (энергетич. уровень системы) принимает вид: 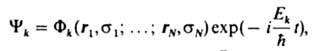где ф-ция Ф_k удовлетворяет ур-нию , к-рое наз. стационарнымур-нием Шрёдингера [Шредингера]. Вероятностная интерпретация квадрата модуля волновой ф-ции, сформулированная в п. 1 осн. постулатов К. м. для состояний системы с дискретным спектром уровней энергии, требует выполнения условия нормировки. Нормировка волновой ф-ции на единицу возможна, если соответствующий интеграл по всему конфигурац. пространству сходится, что имеет место всегда, когда модуль волновой ф-ции достаточно быстро убывает вне нек-рой конечной области (финитное движение). В этом случае энергетич. спектр, т. е. множество уровней энергии, оказывается дискретным, а волновые ф-ции, принадлежащие разл. уровням энергии (в общем случае-разл. собств. значениям эрмитова оператора), оказываются ортогональными: , где _mn=1 при m=п и _mn=0 при тп. В противном случае, когда частицы уходят на сколь угодно большое расстояние, напр., от места их столкновения (инфинитное движение), спектр собств. значений непрерывен, а нормировка и ортогональность волновых ф-ций таких состояний формулируется с помощью 5-ф-ции. Напр., для состояний частицы с определенными импульсами p и р 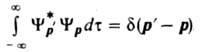Волновая ф-ция, описывающая к.-л. состояние системы, определяется неоднозначно, но все такие описания эквивалентны, т. е. приводят к одинаковым наблюдаемым следствиям. Так, любую волновую ф-цию можно умножить на произвольный фазовый множитель ехр(iа), где - действительная постоянная, не меняя средних значений любых операторов. Далее, любые преобразования систем отсчета, оставляющие инвариантным ур-ние Шрёдингера [Шредингера], преобразуют волновую ф-цию, но все получаемые при этом ее представления будут эквивалентными. И, наконец, волновая ф-ция м. б. задана в разл. формах при разл. представлениях пространства, на к-ром определяются волновые ф-ции; так, волновая ф-ция, заданная как ф-ция пространств. координат, т.е. в конфигурац. (или координатном) представлении, м. б. разложена в интеграл Фурье, так что коэффициенты этого разложения (т.е. ее фурье-образ) будут представлять волновую ф-цию того же состояния в импульсном представлении. Мат. аппарат К. м. определяется прежде всего тем, что наблюдаемые физ. величины представляются эрмитовыми операторами. Разл. соотношения между наблюдаемыми величинами должны сказываться на тех мат. соотношениях, к-рым подчиняются операторы. Если, напр., для рассматриваемого состояния системы волновая ф-ция является собст. ф-цией оператора нек-рой наблюдаемой величины А с собств. значением а, то в этом состоянии измерение величины А будет приводить к одному и тому же значению а. Измерение др. физ. величин F^(k) будет также приводить к определенным значениям f^(k) только в том случае, если эти величины имеют в рассматриваемом состоянии определенные значения. Это возможно, если отвечающие этим величинам операторы коммутируют с оператором , т. е. если выполняется соотношение: . Если же нек-рый операторне коммутирует с А, так что , то не может существовать состояний системы, для к-рых А и В имеют одновременно определенные значения. В частности, не существует состояний, в к-рых координата и импульс частицы имели бы определенные значения, т. к. имеют место соотношения: , где индексы j и k принимают значения 1, 2, 3 и относятся к нумерации переменных: и . Из приведенных коммутационных соотношений для координат и импульсов следует, что в любом состоянии произведение среднеквадратичных разбросов координат r² и импульсов p² для каждой из частиц удовлетворяет соотношению: . Это неравенство наз. соотношениемнеопределенностей для координат и импульсов. Следует подчеркнуть, что в К. м. подобного типа соотношение справедливо также для энергии системы и времени: , где E - разброс в измеряемых значениях энергии, обусловленный взаимод. между измерит, прибором и исследуемой системой, t - длительность процесса измерения. Это же соотношение может иметь и др. смысл: в качестве Е может выступать неопределенность значения энергии нестационарного состояния замкнутой системы, тогда t будет тем характерным для данного состояния временем, за к-рое существенно меняются средние значения физ. величин. Соотношения неопределенностей для координат и импульсов, для энергии и времени имеют важное значение для понимания осн. положений К. м. и их интерпретации. Поэтому эти соотношения часто наз. принципом неопределенности. Совокупность волновых ф-ций в заданном представлении (конфигурационном или импульсном), описывающих стационарные квантовые состояния системы из N частиц, наз. полной, если любая др. волновая ф-ция этой системы м. б. представлена в виде линейной комбинации или ряда, состоящего из таких ф-ций. Волновые ф-ции полной системы являются совместными собств. ф-циями 3N (без учета спина) или 4N (при учете спина) эрмитовых операторов, к-рые коммутируют между собой. Один из этих операторов - гамильтониан. Если одному и тому же уровню энергии системы отвечает неск. состояний, различающихся собств. значениями др. операторов, то такие уровни наз. вырожденными (см. Вырождение энергетических уровней ). Собств. значения ряда операторов либо пропорциональны целым числам, либо выражаются через целые числа. Такие числа наз. квантовыми числами; они часто служат для идентификации состояний квантовомеханич. системы. В ряде случаев набор квантовых чисел позволяет полностью задать состояние системы. Напр., для указания состояния атома водорода достаточно четырех квантовых чисел: главное квантовое число n=1,2,... определяет спектр возможных энергий Е_п=-R/n², где R - постоянная Ридберга, равная 13,6 эВ (109737 см^-1); азимутальное (или орбитальное) квантовое число l=0,1, ..., n—1 (при заданном п) определяет квадрат орбитального (углового) момента ; магн. квантовое число т=-l, -l(-)+1,..., l определяет проекцию орбитального момента на заданную ось; спиновое квантовое число s (- ¹/₂ или -¹/₂) определяет проекцию спина ( или -) на ту же ось. При описании молекул также используются квантовые числа, задающие, напр., состояния отдельных электронов (см. Орбиталь ), возможные значения спина, орбитального и полного моментов, а также колебат. квантовые числа, характеризующие колебат. составляющую полной энергии, и вращат. квантовые числа, характеризующие вращат. составляющую полной энергии молекулы. Точное решение ур-ния Шрёдингера [Шредингера] удается найти лишь в редких случаях. Поэтому важное значение имеют разл. приближенные методы. Если при рассматриваемом движении импульсы частиц достаточно велики, а потенц. энергия их взаимод. изменяется медленно, то применимо квазиклассич. приближение. Оно позволяет, напр., рассчитывать вероятность прохождения частиц и квантовых систем через области пространства, к-рые недоступны для них согласно классич. механике вследствие недостатка энергии (см. Туннельный эффект ). Иногда приближенные волновые ф-ции к.-л. состояния м.б. найдены в виде суперпозиции волновых ф-ций близкой, но более простой системы с коэффициентами, подбираемыми из условия минимума энергии системы (см. Вариационный метод ). Если взаимод. в системе частиц записывается в виде суммы неск. частей, с одной из к-рых точное решение ур-ния Шрёдингера [Шредингера] возможно, а остальные могут рассматриваться как малые возмущения первой, применяют возмущений теорию . Специфич. задачей К. м. является рассмотрение нестационарных волновых ф-ций, соответствующих переходам системы частиц из одного стационарного состояния в другое под влиянием нек-рого возмущения, зависящего от времени.

48. Излучение и поглощение энергии атомами и молекулами.Оптические атомные спектры. Молекулярные спектры. Применение спектрометрии в медицине и биологии.

Атомные спектры, оптические спектры, получающиеся при испускании или поглощении электромагнитного излучения свободными или слабо связанными атомами (например, в газах или парах). Являются линейчатыми, то есть состоят из отдельных спектральных линий, характеризуемых частотой излучения v, которая соответствует квантовому переходу между уровнями энергии E_i и E_k атома согласно соотношению: hv = E_i-E_k где h-постоянная Планка. Спектральные линии можно характеризовать также длиной волны = c/v (с - скорость света), волновым числом = v/c и энергией фотона hv. Частоты спектральных линий выражают в с ^-1, длины волн - в нм и мкм, а также в А, волновые числа - в см -1, энергии фотонов - в эВ. Типичные атомные спектры наблюдаются в видимой, УФ- и ближней ИК-областях спектра. Спектры испускания, или эмиссионные, получают при возбуждении атомов различными способами (фотонами, электронным ударом и т.д.), спектры поглощения, или абсорбционные, - при прохождении электромагнитного излучения, обладающего непрерывным спектром, через атомарные газы или пары. Для наблюдения атомных спектров применяют приборы с фотографической или фотоэлектрической регистрацией.

Атомные спектры обладают ярко выраженной индивидуальностью: каждому элементу соответствует свой спектр нейтрального атома (так называемый дуговой спектр) и свои спектры последовательно образующихся положительных ионов (так называемые искровые спектры). Линии в этих спектрах обозначают римскими цифрами, например линии FeI, FeII, FeIII в спектрах железа соответствуют спектрам Fe, Fe⁺, Fe²⁺.

Вид спектра зависит как от электронного строения данного атома, так и от внешних условий - температуры, давления, напряженностей электрического и магнитного полей и т. п. В зависимости от способа возбуждения атома могут возникать отдельные линии спектра, некоторые его участки, весь спектр нейтрального атома или его иона определенной кратности. Положение линий в таких спектрах подчиняется определенным закономерностям, которые наиболее просты для атомов с одним внешним электроном, то есть для атома Н и нейтральных атомов щелочных металлов, а также изоэлектронных с ними ионов. В спектрах таких атомов наблюдаются спектральные серии, каждая из которых (в случае спектров испускания) получается при возможных квантовых переходах с последовательных вышележащих уровней энергии на один и тот же нижележащий (в спектрах поглощения – при обратных переходах). Промежутки между линиями одной серии убывают в сторону больших частот, то есть линии сходятся к границе серии - максимальной для данной серии частоте, соответствующей ионизации атома. Для атома Н волновые числа линий всех серий с большой точностью определяются обобщенной формулой Бальмера:

где п_k и n_i - значения главного квантового числа для уровней энергии, между которыми происходит квантовый переход, причем n_k, характеризующее нижний уровень энергии, определяет серию, а n_i - ее отдельные линии (при получается граница серии); R-постоянная Ридберга. Аналогичные серии наблюдаются и в спектрах водородоподобных атомов, однако значения волновых чисел для спектральных линий ионов Не⁺ , Li²⁺, ... в Z² раз (Z - пoрядковый номер элемента) больше, чем для соответствующих линий атома Н.

Спектры атомов щелочных металлов, имеющих один электрон на внешней электронной оболочке, схожи со спектром Н, но смещены в область меньших частот; число спектральных линий в них увеличивается, а закономерности в расположении линий усложняются. Пример - спектр Na, атом которого имеет электронную конфигурацию Is²2s²2p⁶3s с легковозбуждаемым внешним электроном 3s. Переходу этого электрона из состояния Зр в состояние 3s соответствует желтая линия Na (дублет = 589,0 нм и = 589,6 нм); это - наиболее яркая линия, с которой начинается так называемая, главная серия Na. Линии этой серии в спектре испускания соответствуют переходам из состояний Зр, 4р, 5р> ... в состояние 3s.

Для атомов последующих групп элементов в периодической системе, обладающих двумя или несколькими внешними электронами, спектры еще более усложняются, что обусловлено взаимодействием электронов. Особенно сложны спектры атомов с заполняющимися d- и f-оболочками; число линий в таких спектрах достигает многих тысяч, простых закономерностей в них не обнаруживается. Однако и для сложных спектров можно произвести систематику оптических квантовых переходов и определить схему уровней энергии. Систематика спектров атомов с двумя и более внеш. Электронами основана на приближенной характеристике отдельных электронов при помощи квантовых чисел n и l с учетом взаимодействия этих электронов друг с другом. При этом приходится учитывать как их электростатического взаимодействия, так и спин-орбитальное, что приводит к расщеплению уровней энергии (так называемая тонкая структура).

В результате этого взаимодействия у большинства атомов каждая спектральная линия представляет собой более или менее тесную группу линий - мультиплет. Так, у всех щелочных металлов наблюдаются двойные линии (дублеты), причем расстояния между линиями увеличиваются с увеличением порядкового номера элемента. Для щелочноземельных элементов наблюдаются одиночные линии (синглеты) и тройные (триплеты). В спектрах атомов последующих групп периодической системы элементов наблюдаются еще более сложные мультиплеты, причем атомам с нечетным числом электронов соответствуют четные мультиплеты (дублеты, квартеты), а с четным числом - нечетные (триплеты, квинтеты). Кроме тонкой структуры в атомных спектрах наблюдается также сверхтонкая структура линий (примерно в 1000 раз уже, чем мультиплетная), обусловленная взаимодействием электронов с магнитными и электрическими моментами ядра.

В атомных спектрах проявляются не все возможные квантовые переходы, а лишь разрешенные правилами отбора. Так, в случае атома с одним внеш. электроном разрешены лишь переходы между уровнями, для которых орбитальное квантовое число l изменяется на 1 , т. е. s-уровни (l = 0) комбинируют с р-уровнями (l=1), р-уровни - с d-уровнями (l = 2) и т.д. Количественная характеристика разрешенного оптического квантового перехода - его вероятность, определяющая интенсивность спектральной линии, соответствующей этому переходу. Вероятности переходов в простейших случаях могут быть рассчитаны методами квантовой механики.

Под влиянием внешних электрических и магнитных полей происходит расщепление спектральных линий. Возмущающие факторы, существующие в излучающей среде, вызывают уширение и сдвиг спектральных линий.

Методы, основанные на измерении частот и интенсивностей линий в спектре, применяют для решения различных задач спектроскопии: проведения общей систематики спектров многоэлектронных атомов; определения уровней энергии таких атомов (это существенно, в частности, при квантово-химических расчетах); нахождения вероятностей переходов и времен жизни возбужденных состояний; изучения механизмов возбуждения атомов; измерения ядерных моментов и т. п. Индивидуальность атомные спектры используют для качественного определения элементного состава вещества, а зависимость интенсивности линий от концентрации излучающих атомов - для количественного анализа.

Исследования атомных спектров сыграли важнейшую роль в развитии представлений о строении атома.

Тема. Строение атома. Оптические спектры атома

Экспериментальная часть

Цели

1. Определить экспериментальным путём характеристическое излучение атома в возбуждённом состоянии.

2. Определить, каким переходом наружного электрона обусловлен характеристический цвет излучения.

Оборудование: фарфоровая чашка, 5-6 мл спирта, шпатель, натрий.

Таблица 1.1

Энергия наружных электронов водорода и s- элементов на различных энергетических уровнях, эВ

атомы	Е*1	Е*2	Е*3	Е*4	Е*5	Е*6
Na	3,027	3,547	4,068	4,589	5,11	5,14

Для определения длины волны л =hc/ДЕ, подставляя из таблицы 1.1 значения ДЕ и с в числитель, то получим, что:

л= 1240,8/ ДЕ (нм)

Молекулярные спектры

• Уровни энергии двухатомной молекулы (схема)

Рис. 1 Уровни энергии двухатомной молекулы (схема)

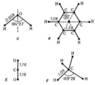• Равновесные конфигурации молекул

Рис. 2 Равновесные конфигурации молекул

• Электронно-колебательный спектр молекулы

Рис. 3 Электронно-колебательный спектр молекулы

• Вращательное расщепление электронно-колебательной полосы

Рис. 4 Вращательное расщепление электронно-колебательной полосы

• Электронные уровни и переходы молекулы бензола (схема)

Рис. 5 Электронные уровни и переходы молекулы бензола (схема)

1–3 из 5

Молекулярные спектры, оптические спектры испускания и поглощения, а также комбинационного рассеяния света, принадлежащие свободным или слабо связанным между собой молекулам. М. с. имеют сложную структуру. Типичные М. с. — полосатые, они наблюдаются в испускании и поглощении и в комбинационном рассеянии в виде совокупности более или менее узких полос в ультрафиолетовой, видимой и близкой инфракрасной областях, распадающихся при достаточной разрешающей силе применяемых спектральных приборов на совокупность тесно расположенных линий. Конкретная структура М. с. различна для различных молекул и, вообще говоря, усложняется с увеличением числа атомов в молекуле. Для весьма сложных молекул видимые и ультрафиолетовые спектры состоят из немногих широких сплошных полос; спектры таких молекул сходны между собой.

М. с. возникают при квантовых переходах между уровнями энергии E‘ и E‘’ молекул согласно соотношению

hn = E‘ — E‘’,     (1)

где hn — энергия испускаемого поглощаемого фотона частоты n (h — Планка постоянная). При комбинационном рассеянии hn равно разности энергий падающего и рассеянного фотонов. М. с. гораздо сложнее линейчатых атомных спектров, что определяется большей сложностью внутренних движений в молекуле, чем в атомах. Наряду с движением электронов относительно двух или более ядер в молекулах происходят колебательное движение ядер (вместе с окружающими их внутренними электронами) около положений равновесия и вращательное движение молекулы как целого. Этим трём видам движений — электронному, колебательному и вращательному — соответствуют три типа уровней энергии и три типа спектров.

Согласно квантовой механике, энергия всех видов движения в молекуле может принимать лишь определённые значения, т. е. она квантуется. Полная энергия молекулы E приближённо может быть представлена в виде суммы квантованных значений энергий трёх видов её движения:

E = E_эл + E_кол + E_вращ.     (2)

По порядку величин

где m — масса электрона, а величина М имеет порядок массы ядер атомов в молекуле, т. е. m/М ~ 10^-3—10^-5, следовательно:

E_эл >> E_кол >> E_вращ.     (4)

Обычно E_эл порядка нескольких эв (несколько сотен кдж/моль), E_кол ~ 10^-2—10^-1 эв, E_вращ ~ 10^-5—10^-3 эв.

В соответствии с (4) система уровней энергии молекулы характеризуется совокупностью далеко отстоящих друг от друга электронных уровней (различные значения E_эл при E_кол = E_вращ = 0), значительно ближе друг к другу расположенных колебательных уровней (различные значения E_кол при заданном E_л и E_вращ = 0) и ещё более близко расположенных вращательных уровней (различные значения E_вращ при заданных E_эл и E_кол). На рис. 1 приведена схема уровней двухатомной молекулы; для многоатомных молекул система уровней ещё более усложняется.

Электронные уровни энергии (E_эл в (2) и на схеме рис. 1 соответствуют равновесным конфигурациям молекулы (в случае двухатомной молекулы характеризуемым равновесным значением r₀ межъядерного расстояния r, см. рис. 1 в ст. Молекула). Каждому электронному состоянию соответствуют определённая равновесная конфигурация и определённое значение E_эл; наименьшее значение соответствует основному уровню энергии.

Набор электронных состояний молекулы определяется свойствами её электронной оболочки. В принципе значения E_эл можно рассчитать методами квантовой химии, однако данная задача может быть решена только с помощью приближённых методов и для сравнительно простых молекул. Важнейшую информацию об электронных уровнях молекулы (расположение электронных уровней энергии и их характеристики), определяемую её химическим строением, получают, изучая её М. с.

Весьма важная характеристика заданного электронного уровня энергии — значение квантового числа S, характеризующего абсолютную величину полного спинового момента всех электронов молекулы. Химически устойчивые молекулы имеют, как правило, чётное число электронов, и для них S = 0, 1, 2... (для основного электронного уровня типично значение S = 0, а для возбуждённых — S = 0 и S = 1). Уровни с S = 0 называются синглетными, с S = 1 — триплетными (т. к. взаимодействие в молекуле приводит к их расщеплению на c = 2S + 1 = 3 подуровня; см. Мультиплетность). Радикалы свободные имеют, как правило, нечётное число электронов, для них S = ¹/₂, ³/₂, ... и типично как для основного, так и для возбуждённых уровней значение S = ¹/₂ (дублетные уровни, расщепляющиеся на c = 2 подуровня).

Для молекул, равновесная конфигурация которых обладает симметрией, электронные уровни можно дополнительно классифицировать. В случае двухатомных и линейных трёхатомных молекул, имеющих ось симметрии (бесконечного порядка), проходящую через ядра всех атомов (см. рис. 2, б), электронные уровни характеризуются значениями квантового числа l, определяющего абсолютную величину проекции полного орбитального момента всех электронов на ось молекулы. Уровни с l = 0, 1, 2, ... обозначаются соответственно S, П, D..., а величина c указывается индексом слева вверху (например, ³S, ²p, ...). Для молекул, обладающих центром симметрии, например CO₂ и C₆H₆ (см. рис. 2, б, в), все электронные уровни делятся на чётные и нечётные, обозначаемые индексами g и u (в зависимости от того, сохраняет ли волновая функция знак при обращении в центре симметрии или меняет его).

Колебательные уровни энергии (значения Е_кол) можно найти квантованием колебательного движения, которое приближённо считают гармоническим. В простейшем случае двухатомной молекулы (одна колебательная степень свободы, соответствующая изменению межъядерного расстояния r) её рассматривают как гармонический осциллятор; его квантование даёт равноотстоящие уровни энергии:

E_кол = hn_e (u +1/2),     (5)

где n_e — основная частота гармонических колебаний молекулы, u — колебательное квантовое число, принимающее значения 0, 1, 2, ... На рис. 1 показаны колебательные уровни для двух электронных состояний.

Для каждого электронного состояния многоатомной молекулы, состоящей из N атомов (N ³ 3) и имеющей f колебательных степеней свободы (f = 3N — 5 и f = 3N — 6 для линейных и нелинейных молекул соответственно), получается f т. н. нормальных колебаний с частотами n_i (i = 1, 2, 3, ..., f) и сложная система колебательных уровней:

где u_i = 0, 1, 2, ... — соответствующие колебательные квантовые числа. Набор частот нормальных колебаний в основном электронном состоянии является очень важной характеристикой молекулы, зависящей от её химического строения. В определённом нормальном колебании участвуют все атомы молекулы или часть их; атомы при этом совершают гармонические колебания с одной частотой v_i, но с различными амплитудами, определяющими форму колебания. Нормальные колебания разделяют по их форме на валентные (при которых изменяются длины линий связи) и деформационные (при которых изменяются углы между химическими связями — валентные углы). Число различных частот колебаний для молекул низкой симметрии (не имеющих осей симметрии порядка выше 2) равно 2, и все колебания являются невырожденными, а для более симметричных молекул имеются дважды и трижды вырожденные колебания (пары и тройки совпадающих по частоте колебаний). Например, у нелинейной трёхатомной молекулы H₂O (рис. 2, а) f = 3 и возможны три невырожденных колебания (два валентных и одно деформационное). Более симметричная линейная трёхатомная молекула CO₂ (рис. 2, б) имеет f = 4 — два невырожденных колебания (валентных) и одно дважды вырожденное (деформационное). Для плоской высокосимметричной молекулы C₆H₆ (рис. 2, в) получается f = 30 — десять невырожденных и 10 дважды вырожденных колебаний; из них 14 колебаний происходят в плоскости молекулы (8 валентных и 6 деформационных) и 6 неплоских деформационных колебаний — перпендикулярно этой плоскости. Ещё более симметричная тетраэдрическая молекула CH₄ (рис. 2, г) имеет f = 9 — одно невырожденное колебание (валентное), одно дважды вырожденное (деформационное) и два трижды вырожденных (одно валентное и одно деформационное).

Вращательные уровни энергии можно найти квантованием вращательного движения молекулы, рассматривая её как твёрдое тело с определёнными моментами инерции. В простейшем случае двухатомной или линейной многоатомной молекулы её энергия вращения

где I — момент инерции молекулы относительно оси, перпендикулярной оси молекулы, а М — вращательный момент количества движения. Согласно правилам квантования,

где вращательное квантовое число J = 0, 1, 2, ..., и, следовательно, для E_вращ получили:

где вращательная постоянная  определяет масштаб расстояний между уровнями энергии, уменьшающийся с увеличением масс ядер и межъядерных расстояний. На рис. 1 показаны вращательные уровни для каждого электронно-колебательного состояния.

Различные типы М. с. возникают при различных типах переходов между уровнями энергии молекул. Согласно (1) и (2)

DE = E‘ — E‘’ = DE_эл + DE_кол + DE_вращ, (8)

где изменения DE_эл, DE_кол и DE_вращ электронной, колебательной и вращательной энергий удовлетворяют условию:

DE_эл >> DE_кол >> DE_вращ     (9)

[расстояния между уровнями того же порядка, что и сами энергии E_эл, E_ол и E_вращ, удовлетворяющие условию (4)].

При DE _эл ¹ 0 получаются электронные М. с., наблюдаемые в видимой и в ультрафиолетовой (УФ) областях. Обычно при DE_эл ¹ 0 одновременно DE_кол ¹ 0 и DE_вращ ¹ 0; различным DE_кол при заданном DE_эл соответствуют различные колебательные полосы (рис. 3), а различным DE_вращ при заданных DE_эл и DE_кол — отдельные вращательные линии, на которые распадается данная полоса; получается характерная полосатая структура (рис. 4). Совокупность полос с заданным DE_эл (соответствующим чисто электронному переходу с частотой v_эл = DE_эл/h) называемая системой полос; отдельные полосы обладают различной интенсивностью в зависимости от относительных вероятностей переходов (см. Квантовые переходы), которые могут быть приближённо рассчитаны квантовомеханическими методами. Для сложных молекул полосы одной системы, соответствующие данному электронному переходу, обычно сливаются в одну широкую сплошную полосу, могут накладываться друг на друга и несколько таких широких полос. Характерные дискретные электронные спектры наблюдаются в замороженных растворах органических соединений (см. Шпольского эффект). Электронные (точнее, электронно-колебательно-вращательные) спектры изучаются экспериментально при помощи спектрографов и спектрометров со стеклянной (для видимой области) и кварцевой (для УФ-области) оптикой, в которых для разложения света в спектр применяются призмы или дифракционные решётки (см. Спектральные приборы).

При DE_эл = 0, а DE_кол ¹ 0 получаются колебательные М. с., наблюдаемые в близкой (до нескольких мкм) и в средней (до нескольких десятков мкм) инфракрасной (ИК) области, обычно в поглощении, а также в комбинационном рассеянии света. Как правило, одновременно DE_вращ ¹ 0 и при заданном E_кол получается колебательная полоса, распадающаяся на отдельные вращательные линии. Наиболее интенсивны в колебательных М. с. полосы, соответствующие Du = u’ — u’’ = 1 (для многоатомных молекул — Du_i = u_i’ — u_i’’= 1 при Du_k = u_k’ — u_k’’ = 0, где k ¹ i).

Для чисто гармонических колебаний эти отбора правила, запрещающие др. переходы, выполняются строго; для ангармонических колебаний появляются полосы, для которых Du > 1 (обертоны); их интенсивность обычно мала и убывает с увеличением Du.

Колебательные (точнее, колебательно-вращательные) спектры изучаются экспериментально в ИК-области в поглощении при помощи ИК-спектрометров с призмами, прозрачными для ИК-излучения, или с дифракционными решётками, а также Фурье-спектрометров и в комбинационном рассеянии при помощи светосильных спектрографов (для видимой области) с применением лазерного возбуждения.

При DE_эл = 0 и DE_кол = 0 получаются чисто вращательные М. с., состоящие из отдельных линий. Они наблюдаются в поглощении в далёкой (сотни мкм)ИК-области и особенно в микроволновой области, а также в спектрах комбинационного рассеяния. Для двухатомных и линейных многоатомных молекул (а также для достаточно симметричных нелинейных многоатомных молекул) эти линии равно отстоят (в шкале частот) друг от друга с интервалами Dn = 2B в спектрах поглощения и Dn = 4B в спектрах комбинационного рассеяния.

Чисто вращательные спектры изучают в поглощении в далёкой ИК-области при помощи ИК-спектрометров со специальными дифракционными решётками (эшелеттами) и Фурье-спектрометров, в микроволновой области при помощи микроволновых (СВЧ) спектрометров (см. Микроволновая спектроскопия), а также в комбинационном рассеянии при помощи светосильных спектрографов.

Методы молекулярной спектроскопии, основанные на изучении М. с., позволяют решать разнообразные задачи химии, биологии и др. наук (например, определять состав нефтепродуктов, полимерных веществ и т. п.). В химии по М. с. изучают структуру молекул. Электронные М. с. дают возможность получать информацию об электронных оболочках молекул, определять возбуждённые уровни и их характеристики, находить энергии диссоциации молекул (по схождению колебательных уровней молекулы к границам диссоциации). Исследование колебательных М. с. позволяет находить характеристические частоты колебаний, соответствующие определённым типам химических связей в молекуле (например, простых двойных и тройных связей С—С, связей С—Н, N—Н, О—Н для органических молекул), различных групп атомов (например, CH₂, CH₃, NH₂), определять пространственную структуру молекул, различать цис- и транс-изомеры. Для этого применяют как инфракрасные спектры поглощения (ИКС), так и спектры комбинационного рассеяния (СКР). Особенно широкое распространение получил метод ИКС как один из самых эффективных оптических методов изучения строения молекул. Наиболее полную информацию он даёт в сочетании с методом СКР. Исследование вращательных М. с., а также вращательной структуры электронных и колебательных спектров позволяет по найденным из опыта значениям моментов инерции молекул [которые получаются из значений вращательных постоянных, см. (7)] находить с большой точностью (для более простых молекул, например H₂O) параметры равновесной конфигурации молекулы — длины связей и валентные углы. Для увеличения числа определяемых параметров исследуют спектры изотопических молекул (в частности, в которых водород заменен дейтерием), имеющих одинаковые параметры равновесных конфигураций, но различные моменты инерции.

В качестве примера применения М. с. для определения химического строения молекул рассмотрим молекулу бензола C₆H₆. Изучение её М. с. подтверждает правильность модели, согласно которой молекула плоская, а все 6 связей С—С в бензольном кольце равноценные и образуют правильный шестиугольник (рис. 2, б), имеющий ось симметрии шестого порядка, проходящую через центр симметрии молекулы перпендикулярно её плоскости. Электронный М. с. поглощения C₆H₆ состоит из нескольких систем полос, соответствующих переходам из основного чётного синглетного уровня на возбуждённые нечётные уровни, из которых первый является триплетным, а более высокие — синглетными (рис. 5). Наиболее интенсивна система полос в области 1840  (E₅ — E₁= 7,0 эв), наиболее слаба система полос в области 3400  (E₂ — E₁ = 3,8 эв), соответствующая синглетно-триплетному переходу, запрещенному приближёнными правилами отбора для полного спина. Переходы соответствуют возбуждению т. н. p-электронов, делокализованных по всему бензольному кольцу (см. Молекула); полученная из электронных молекулярных спектров схема уровней рис. 5 находится в согласии с приближёнными квантовомеханическими расчётами. Колебательные М. с. C₆H₆ соответствуют наличию в молекуле центра симметрии — частоты колебаний, проявляющиеся (активные) в ИКС, отсутствуют (неактивные) в СКР и наоборот (т. н. альтернативный запрет). Из 20 нормальных колебаний C₆H₆ 4 активны в ИКС и 7 активны в СКР, остальные 11 неактивны как в ИКС, так и в СКР. Значения измеренных частот (в см^-1): 673, 1038, 1486, 3080 (в ИКС) и 607, 850, 992, 1178, 1596, 3047, 3062 (в СКР). Частоты 673 и 850 соответствуют неплоским колебаниям, все остальные частоты — плоским колебаниям. Особо характерны для плоских колебаний частота 992 (соответствующая валентному колебанию связей С—С, состоящему в периодическом сжатии и растяжении бензольного кольца), частоты 3062 и 3080 (соответствующие валентным колебаниям связей С—Н) и частота 607 (соответствующая деформационному колебанию бензольного кольца). Наблюдаемые колебательные спектры C₆H₆ (и аналогичные им колебательные спектры C₆D₆) находятся в очень хорошем согласии с теоретическими расчётами, позволившими дать полную интерпретацию этих спектров и найти формы всех нормальных колебаний.

Подобным же образом можно при помощи М. с. определять структуру разнообразных классов органических и неорганических молекул, вплоть до весьма сложных, например молекул полимеров.

49. Оптические Квантовые генераторы(лазеры).Основные свойства лазерного излучения. Применение лазеров а биологических исследованиях и медецине.Лазерные препараты для коагуляции и обработки тканей.