Разложение Шеннона

Теорема. Каждая булева функция f(x₁,x₂,…,x_n) может быть представлена в виде разложения Шеннона:

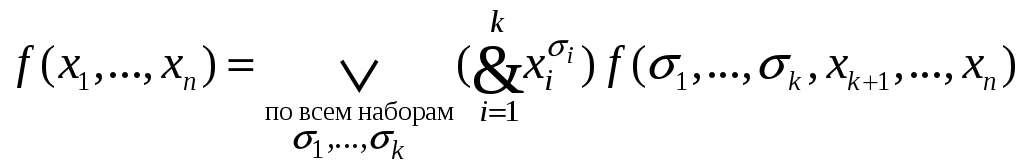
Пусть. Рассмотрим разложение функции f(x₁,x₂, x₃,x₄,x₅) по x₁,x₂:

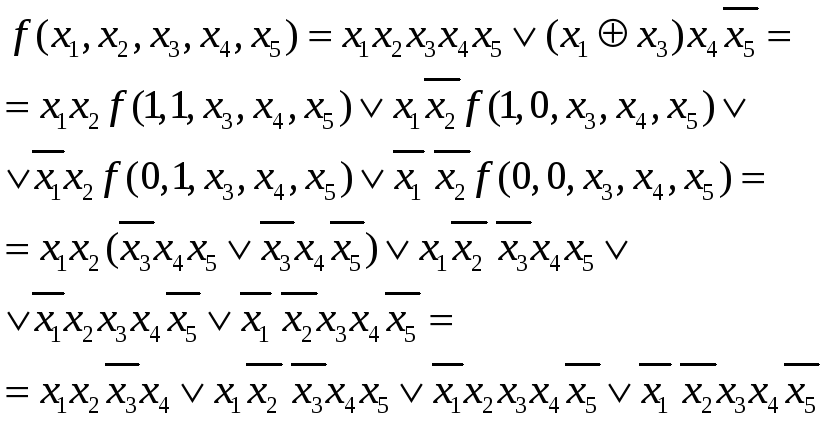
Два предельных случая разложения Шеннона: разложение по одной переменной и разложение по всем переменным. В последнем случае получаем СДНФ.

Полнота систем функций. Базисы

Суперпозицией системы функций называется любая функция f, получаемая

1. из S переименованием переменных,

2. подстановкой вместо некоторых переменных функции функций _jS.

3. Многократным применением суперпозиции.

Например, . Тогда

1.

2.

3.

Замыканием [K] множества функций K алгебры логики называется множество всех функций алгебры логики, являющихся суперпозициями множества функций из K.

Множество функций K называется (функционально) замкнутым, если [K]=K. Замкнутые множества функций так же называют замкнутыми классами.

Подмножество Р замкнутого множества K называется функционально полным в K, если [P]=K. Функционально полное множество называется базисом, если никакое его подмножество функционально полным не является.

Класс Р₂ – класс всех булевых функций.

Функции f₁ и f₂ называются конгруэнтными, если одна из них может быть получена из другой переименованием переменных (без отождествления).

Например, конгруэнтны функции и , а так же функция конгруэнтна функции . При рассмотрении класса обычно указывается одна из конгруэнтных функций.

Функция называется сохраняющей 0, если .

Класс функций, сохраняющих 0: К₀={|}. Класс функций К₀ является замкнутым классом, при любой подстановке переменных и функций, сохраняющих 0, в функцию, сохраняющую 0, получаем функцию, сохраняющую 0.

Рассмотрим функцию . Она принадлежит классу К₀, т.к. . Если же проверим функцию, то , поэтому она не принадлежит классу К₀.

Если функция задана таблицей истинности, то проверка принадлежности классу К₀ сводится к проверке значения функции в первой строке (аргументы располагаются в порядке возрастания числовых эквивалентов, поэтому в первой строке находится набор из одних 0): если значение функции равно 0, то она принадлежит классу К₀, в противном случае она не принадлежит этому классу.

Функция называется сохраняющей 1, если .

Класс функций, сохраняющих 1: К₁={|}. Класс функций К₁ является замкнутым классом, при любой подстановке переменных и функций, сохраняющих 1, в функцию, сохраняющую 1, получаем функцию, сохраняющую 1.

Функция принадлежит классу К₁, Функция не принадлежит этому классу.

Если функция задана таблицей истинности, то проверка принадлежности классу К₁ сводится к проверке значения функции в последней строке (аргументы располагаются в порядке возрастания числовых эквивалентов, поэтому в последней строке находится набор из одних 1): если значение функции равно 1, то она принадлежит классу К₁, в противном случае она не принадлежит этому классу.

Функция называется двойственной к функции , если

.

Найдем функцию, двойственную к функции .

Функция называется самодвойственной, если . Рассмотренная выше функция самодвойственной не является.

Класс самодвойственных функций К_с=.

Класс К_с так же является замкнутым классом. При подстановке в самодвойственную функцию переменных и самодвойственных функций полученная функция так же будет самодвойственной.

Если функция задана таблицей истинности, то проверка принадлежности классу К_с производится сопоставлением значений функции на противоположных наборах. Поскольку аргументы располагаются в порядке возрастания числовых эквивалентов, противоположные наборы располагаются симметрично относительно линии, разделяющей таблицу пополам. Противоположным наборам аргументов должны соответствовать противоположные значения функции. Функция принадлежит классу К_с, если всем противоположным наборам соответствуют противоположные значения, если хотя бы одной паре противоположных наборов соответствуют одинаковые значения функции, то она не принадлежит классу К_с.

Рассмотрим пример:

x1	x2	x3	F(x1,x2,x3)
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Эта функция не является самодвойственной, нарушения самодвойственности - F(0,0,0)= F(1,1,1), и F(0,0,1)= F(1,1,0).

Функция является линейной, если . Имеется в виду суммирование по модулю 2.

Класс линейных функций К_л= {|}.

Класс линейных функций К_л так же является замкнутым. При подстановке линейных функций вместо аргументов линейной функции получается так же линейная функция. Это обусловлено дистрибутивностью конъюнкции относительно жегалкинского сложения.

Проверка линейности функции является довольно трудоёмкой. Можно построить полином Жегалкина для функции, и если он будет содержать нелинейные члены, то она будет нелинейной. Другой вариант проверки – предположить, что функция линейна, найти коэффициенты, для чего используются значение функции, а на оставшихся наборах проверить, имеет ли функция требуемый вид.

Предполагаем, что функция линейная, . Тогда =с₀. Далее, =с₀с₁. Определяем значение по таблице истинности, и, поскольку с₀ известно, определяется с₁. И далее, =с₀с_i. На оставшихся наборах проверяем, имеет ли функция предположенный вид.

Рассмотрим пример:

x1	x2	x3	F(x1,x2,x3)
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Предполагаем, что функция линейна, тогда имеет вид: F(x₁,x₂,x₃)= с₀ с₁ x₁ с₂ x₂  с₃x₃.

F(0,0,0)= с₀=1,

F(1,0,0)= с₀ с₁=1 с₁=1, откуда с₁=0.

F(0,1,0)= с₀  с₂ =1 с₂=1, откуда с₂=0.

F(0,0,1)= с₀ с₃ =с₀  с₃=0, откуда с₃=1. Таким образом, получаем вид функции:

F(x₁,x₂,x₃)= 1 x₃. Проверяем значения на других наборах:

F(0,1,1)= 1 1=0, что совпадает со значением в таблице.

F(1,0,1)= 1 1=0, что совпадает со значением в таблице

F(1,1,0)= 1 0=1, что не совпадает со значением в таблице, поэтому анализируемая функция не линейна.

Класс монотонных (изотонных функций) K_M:

=

где .

Класс монотонных функций является замкнутым. При подстановке монотонных функций и отождествлении переменных в монотонной функции функция остаётся монотонной.

Для проверки монотонности достаточно сравнить значения функции для соседних наборов аргументов. Проверку можно осуществить с помощью представления функции на гиперкубе соответствующей размерности.

Вид гиперкуба размерности 3 представлен на рисунке.

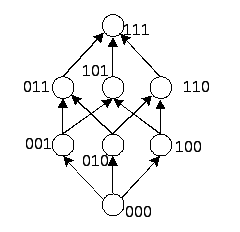
Для анализа монотонности функций в вершинах гиперкуба проставляются значение функции. Пример анализа функции на монотонность приведён на рисунке.

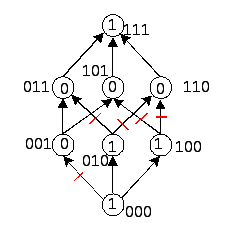
Перечёркнутые стрелки соответствуют нарушению монотонности функции. Таким образом, анализируемая функция монотонной не является.

Критерий Поста-Яблонского.

Система функций S является полной в Р₂ тогда и только тогда, когда в S есть хотя бы одна функция, не принадлежащая классу К₀, хотя бы одна функция, не принадлежащая классу К₁, хотя бы одна функция, не принадлежащая классу К_Л, хотя бы одна функция, не принадлежащая классу К_М, хотя бы одна функция, не принадлежащая классу К_С.