2. Отношение упорядоченности

Бинарное отношение, заданное на множестве М и обладающее свойствами рефлексивности, транзитивности и антисимметричности, называется отношением частичной упорядоченности или просто упорядоченностью. Множество М в этом случае называется упорядоченным. Упорядоченность называется строгой, если отношение не рефлексивно. Упорядоченность называется линейной, если для любых элементов а, b  М => либо (a,b)Р, либо (b,a)Р. Множество М в этом случае называется линейно–упорядоченным или цепью.

Для обозначения отношения упорядоченности обычно используют знаки  (или ),  (или ). При этом ab равнозначно ba, и запись a<b означает, что ab и ab. Если a<b, то говорят, что а предшествует b (находится перед b), а b следует за а (находится после а). Т.о., для любых двух элементов цепи обязательно должно выполняться одно из двух: либо a  b, либо b  a.

Утверждение: если множество М упорядочено или линейно–упорядочено, то и каждое его подмножество упорядочено тем же отношением.

Пусть А  М и М – упорядоченное множество. Элемент хМ называется верхней (нижней) границей множества А, если для  аА => а ≤ х ( х ≤ а ). Множество А в этом случае называется ограниченным сверху (снизу). Естественно, что А может иметь не одну верхнюю (нижнюю) границу, а множество верхних (нижних) границ. Тогда наименьшая из верхних границ А называется верхней гранью множества А и обозначается sup(А) – супремум. Аналогично, наибольшая из нижних границ множества А называется нижней гранью А и обозначается inf(А) – инфимум. (Иначе говоря, верхняя грань А есть нижняя граница множества всех верхних границ А, а нижняя грань А есть верхняя граница множества всех нижних границ А.)

Линейно–упорядоченное множество называется вполне упорядоченным, если у каждого его непустого и ограниченного снизу подмножества есть нижняя грань. Иными словами, упорядоченное множество является вполне упорядоченным, если любое его непустое подмножество имеет первый элемент.

Для графического изображения конечных частично или линейно упорядоченных множеств служит диаграмма Хассе.

Пусть М – упорядоченное множество и элементы x, yM, причем x<y. Говорят, что y покрывает x, если не существует элемента zM такого, что x  z y.

Н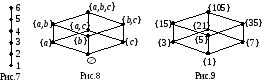 а диаграмме Хассе элементы множества М изображаются в виде точек. Две точки x и y соединяются отрезком прямой в том и только том случае, когда y покрывает x. При этом точку x рисуют ниже точки y.

Примеры.

1) M ={ 1, 2, 3, 4, 5, 6 } упорядочено отношением . Тогда его диаграмма выглядит так, как показано на рисунке 7. Такая диаграмма характерна для линейно упорядоченных множеств.

2) M = 2^{{ a, b, c }} = { , { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }} упорядочено отношением включения – «  ». Тогда его диаграмма выглядит как на рисунке 8.

3) M ={ 1, 3, 5, 7, 15, 21, 35, 105 } упорядочено отношением P={ (x, y) : y делится на x }. Его диаграмма Хассе изображена на рисунке 9 и совпадает с предыдущей диаграммой с точностью до обозначения элементов. Между элементами этих множеств можно установить биективное отображение, сохраняющее имеющуюся упорядоченность элементов. Говорят, что такие множества изоморфны (подобны) между собой относительно заданных на них отношений порядка.