- •Матан часть 2.Производные и тд.
- •2.)Основные правила дифференцирования. Производная обратной функции. Логарифмическое дифференцирование.
- •2Теорема
- •3.)Определение дифференцируемой функции. Связь дифференцируемости функции с существованием производной.
- •4.)Дифференциал функции: определение, геометрический смысл. Свойства дифференциала. Инвариантность формы записи первого дифференциала. Дифференцирование функций, заданных параметрически.
- •5. )Производные высших порядков: определение, производные высших порядков для суммы, произведения (формула Лейбница). Физический смысл второй производной.
- •7.)Основные теоремы дифференциального исчисления (теоремы Ролля, Лагранжа, Коши; все с доказательством).
- •1. Теорема Ролля
- •3. Теорема Коши
- •8.)Правило Лопиталя.
- •9.)Возрастание и убывание функции. Необходимое и достаточное условие возрастания (убывания) дифференцируемой функции.
- •10.)Экстремумы функции: определение, необходимое условие экстремума (Теорема Ферма). Достаточные условия экстремума.
- •12.)Асимптоты кривой: определение, виды, нахождение.
8.)Правило Лопиталя.
Пусть x0Îℝ̄ и выполняются следующие условия:
![]() 1) функции
f(x)
и j(x)
определены и непрерывны в некоторой
d-окрестности
x0,
за исключением возможно самой x0;
1) функции
f(x)
и j(x)
определены и непрерывны в некоторой
d-окрестности
x0,
за исключением возможно самой x0;
![]() или
или
3![]() )
функции f(x)
и j(x)
дифференцируемы в U*(x0,d) ,
причем
)
функции f(x)
и j(x)
дифференцируемы в U*(x0,d) ,
причем
![]() j ¢(x) ¹ 0 , "xÎU*(x0,d)
.
j ¢(x) ¹ 0 , "xÎU*(x0,d)
.
Тогда, если (конечный или бесконечный), то
![]() причем
эти два предела будут равны. Т.е.
причем
эти два предела будут равны. Т.е.
Правило
Лопиталя можно применять только при
раскрытии неопределенности вида ![]() и
и ![]()
Замечания.
1) Если f ¢(x) и j ¢(x) тоже являются б.м. (б.б.) при x ® x0 , то правило Лопиталя можно применить повторно.
![]()
2![]() )
Если не существует, то
правило Лопиталя непри-
)
Если не существует, то
правило Лопиталя непри-
менимо. При этом может существовать.
9.)Возрастание и убывание функции. Необходимое и достаточное условие возрастания (убывания) дифференцируемой функции.
Необходимое условие: Если дифференцируемая на отрезке [a,b] функция F(x) возрастает (убывает), то F’(x)0 (F’(x) 0) для х [a,b].
Необходимое условие:
Пусть F(x) возрастает на отрезке [a,b]. Придадим аргументу х приращение х и рассмотрим отношение
F(x+х)- F(x)/ х (1)
Т.к. F(x) – возрастает, то
F(x+х)> F(x) при х>0;
F(x+х)< F(x) при х<0.
В обоих случаях
F(x+х)- F(x)/ х >0, т.к. числитель и знаменатель одного знака
F’(x)=
![]() (F(x+х)-
F(x)/
х)
0;
(2)
(F(x+х)-
F(x)/
х)
0;
(2)
т.е. F’(x)0. (Если бы было F’(x)<0, то при достаточно малых значениях отношение (1) было бы отрицательным, что противоречит соотношению (2)).
Достаточное условие: Если F(x) дифференцируема на отрезке [a,b] и F(x)>0(F(x)<0) для х [a,b], то эта функция возрастает (убывает) на отрезке [a,b].
Пусть F’(x)>0 при х [a,b].
Возьмем любые точки х1 и х2 из отрезка [a,b] про х1<х2.
По теореме Лагранжа
F(x1)- F(x2)= F’(с)(x1-х2), где с(х1,х2).
По условию F’(с)>0 F(x1)- F(x2)>0, или F(x2)>F(x1), т.е.
функция F(x) на отрезке [a,b] возрастает.
10.)Экстремумы функции: определение, необходимое условие экстремума (Теорема Ферма). Достаточные условия экстремума.
Пусть
![]() ∈
D(f),
∈
D(f),
![]() внутренняя
точка D(f)
(т.е.
внутренняя
точка D(f)
(т.е.
![]() некоторая окрестность точки
некоторая окрестность точки ![]() ,
целиком лежащая во множестве D(f)).
,
целиком лежащая во множестве D(f)).
ОПРЕДЕЛЕНИЕ
Точка
![]() точка максимума функции, если
точка максимума функции, если
![]() такая δ
- окрестность U(
такая δ
- окрестность U(![]() ,
δ)
точки
,
δ)
точки ![]() ,
что f(x)<f(
,
что f(x)<f(![]() ),
),
![]() x
∈
U*(
x
∈
U*(![]() ,
δ).
,
δ).
ОПРЕДЕЛЕНИЕ
Точка
![]() точка минимума функции, если
точка минимума функции, если
![]() такая δ - окрестность U(
такая δ - окрестность U(![]() ,
δ) точки
,
δ) точки ![]() ,
что f(x)>f(
,
что f(x)>f(![]() ),
),
![]() x ∈ U*(
x ∈ U*(![]() ,
δ).
,
δ).
Замечания:
-
«Глобальные» - наибольшее и наименьшее значение
«Локальные» - точки экстремума
-
Некоторые минимумы могут быть больше максимумов

ТЕОРЕМА (необходимое условие экстремума, теорема Ферма)
Пусть
![]() - точка экстремума функции f(x)
и f(x)-дифференцируема
в точке
- точка экстремума функции f(x)
и f(x)-дифференцируема
в точке ![]() .
Тогда f
’(
.
Тогда f
’(![]() )=0.
)=0.
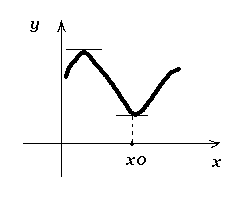
Геометрический смысл:
Если
![]() -
точка экстремума функции f(x)
и кривая y=f(x)
имеет невертикальную касательную в
точке
-
точка экстремума функции f(x)
и кривая y=f(x)
имеет невертикальную касательную в
точке ![]() (
(![]() ,f(
,f(![]() ),
то эта касательная - горизонтальная.
),
то эта касательная - горизонтальная.
Доказательство:
Пусть
x
= ![]() - максимум функции f(x)
- максимум функции f(x)
Δx ≠0
f(![]() +
Δx )
< f(
+
Δx )
< f(![]() );
);
f(![]() +
Δx )
- f(
+
Δx )
- f(![]() )
< 0;
)
< 0;
![]()
y’=![]()
![]()
![]() =
=![]()
![]() ≥
0
≥
0
![]() =
=![]()
![]() ≤
0
≤
0
(≥,≤ - по свойству пределов)
![]()
![]() =0
=0
ОПРЕДЕЛЕНИЕ
Стационарные
точки- точки, в которых ![]() (x)=0.
(x)=0.
Теорема (первое достаточное условие экстремума)
Пусть
![]() внутренняя
точка D(f),
f(x)
непрерывна в U(
внутренняя
точка D(f),
f(x)
непрерывна в U(![]() ,
δ),
f(x)
дифференцируема в U(
,
δ),
f(x)
дифференцируема в U(![]() ,
δ)
или в U*(
,
δ)
или в U*(![]() ,
δ).
,
δ).
Если
при переходе через точку ![]() производная функции меняет знак, то
производная функции меняет знак, то ![]() - точка экстремума. При этом, если
производная меняет знак с «+» на «-» , то
- точка экстремума. При этом, если
производная меняет знак с «+» на «-» , то
![]() -
точка максимума, если с «-» на «+», то
-
точка максимума, если с «-» на «+», то![]() -
точка минимума.
-
точка минимума.
Доказательство:
Предположим сначала, что производная
меняет знак с «+» на «-»,
т.е. что для всех x,
достаточно
близких к точке ![]() ,
имеем
,
имеем
f
‘(x)
> 0 при x
<![]()
f
’(x)
< 0 при x
![]()
Применяя
теорему Лагранжа к разности f(x)
- f(![]() ,
получим
,
получим
f(x)
- f(![]() =f
‘(ξ)
(x-
=f
‘(ξ)
(x-![]() ,
где ξ-точка,лежащая между x
и
,
где ξ-точка,лежащая между x
и![]()
-
Пусть x<
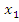 ,
тогда
,
тогда
ξ<
![]() ,
f
‘(ξ)
>
0, f ‘(ξ)
(x-
,
f
‘(ξ)
>
0, f ‘(ξ)
(x-![]() < 0
< 0
следовательно,
f(x)
- f(![]() < 0
< 0
![]()
-
Пусть x
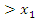 ,
тогда
,
тогда
ξ
> ![]() ,
f
‘(ξ)
<
0, f ‘(ξ)
(x-
,
f
‘(ξ)
<
0, f ‘(ξ)
(x-![]() < 0
< 0
следовательно,
f(x)
- f(![]() < 0
< 0
![]()
Соотношения
(1) и (2) показывают, что для всех значений
x,
достаточно
близких к ![]() ,
значения функции меньше, чем значение
функции в точке
,
значения функции меньше, чем значение
функции в точке ![]() Следовательно, в точке
Следовательно, в точке
![]() функция
функция
![]() имеет максимум.
имеет максимум.
Замечание: Точками экстремума могут быть не только стационарные точки, в которых функция не имеет производной ( точки разрыва производной).
Стационарные точки и точки, в которых производная не существует - критические точки 1 рода.
Теорема (второе достаточное условие экстремума)
Пусть
![]() внутренняя
точка D(f)
и f(x)
n
раз дифференцируема в точке
внутренняя
точка D(f)
и f(x)
n
раз дифференцируема в точке ![]() ,
,
f
‘(![]() =f
‘’(
=f
‘’(![]() =…=
=…=![]() (
(![]() =0,
=0,
![]() (
(![]() ≠0.
≠0.
Тогда:
-
Если n- четное и
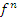 (
(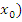 >0,
то
>0,
то 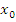 -
минимум.
-
минимум. -
Если n- четное и
 (
( <0,
то
<0,
то 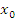 -
минимум.
-
минимум. -
Если n-нечетное, то
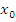 не является точкой экстремума.
не является точкой экстремума.
11.)Выпуклость и вогнутость кривой, точки перегиба: определения, необходимое и достаточное условия выпуклости (вогнутости) кривой y=f(x) , необходимые и достаточные условия перегиба кривой y=f(x) .
ОПРЕДЕЛЕНИЕ. Пусть ℓ – кривая, M0 – точка кривой, причем в M0 существует невертикальная касательная к ℓ.
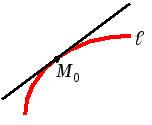 Кривую
ℓ называют
выпуклой
в точке
M0,
если в
некоторой окрестности этой точки кривая
лежит ниже касательной,
проведенной
к
ℓ в точке
M0.
Кривую
ℓ называют
выпуклой
в точке
M0,
если в
некоторой окрестности этой точки кривая
лежит ниже касательной,
проведенной
к
ℓ в точке
M0.
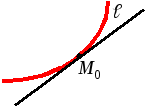 Кривую
ℓ называют
вогнутой
в точке
M0,
если в
некоторой окрестности этой точки кривая
лежит выше касательной,
проведенной
к ℓ в
точке M0.
Кривую
ℓ называют
вогнутой
в точке
M0,
если в
некоторой окрестности этой точки кривая
лежит выше касательной,
проведенной
к ℓ в
точке M0.
Точки кривой, которые разделяют ее выпуклые и вогнутые участки, называются точками перегиба кривой.
Замечания.
1) Выпуклость и вогнутость кривой в точке – локальные понятия. Они определяют относительное расположение точек кривой и касательной вблизи точки касания. В точках, удаленных от точки касания, кривая и касательная могут располагаться произвольным образом.
2
 ) В
точке перегиба касательная к кривой
(если она существует) пересекает кривую
(кривая переходит с одной стороны
касательной на другую)
) В
точке перегиба касательная к кривой
(если она существует) пересекает кривую
(кривая переходит с одной стороны
касательной на другую)
.
ОПРЕДЕЛЕНИЕ. Кривая y = f(x) называется выпуклой (вогнутой) на интервале (a;b) если "xÎ (a;b) кривая выпукла (вогнута) в соответствующей точке M(x ; f(x)).
Замечания.
1) Если M0(x0 ; f(x0)) – точка перегиба кривой y = f(x), то x0 – внутренняя точка области определения функции f(x).
2) Точками перегиба кривой y = f(x) часто называют точки, которые разделяют интервалы выпуклости и вогнутости этой кривой (т.е. абсциссы точек перегиба кривой y = f(x)).
ТЕОРЕМА (необходимое и достаточное условия выпуклости (вогнутости) графика функции).
Пусть функция y = f(x) дважды дифференцируема на интервале (a;b). Тогда:
1) если кривая y = f(x) выпукла (вогнута) на интервале (a;b), то f ¢¢(x) £ 0 (f ¢¢(x) ³ 0), "xÎ (a;b)
(необходимое условие выпуклости (вогнутости) графика);
2) если f ¢¢(x) < 0 (f ¢¢(x) > 0) "xÎ (a;b),
то кривая y = f(x) выпукла (вогнута) на интервале (a;b)
(достаточное
условие выпуклости (вогнутости) графика)

Доказательство. Возьмем в интервале (a, b) произвольную точку х=х0 и проведем касательную к кривой в точке с абсциссой х—х0. Теорема будет доказана, если мы установим, что все точки кривой на интервале (а, b) лежат ниже этой касательной, т.е. что ордината любой точки кривой y = f(x) меньше ординаты у касательной при одном и том же значении х.
Уравнение кривой имеет вид
V = f(x). (1)
Уравнение же касательной к кривой в точке х = х0 имеет вид
ỹ -f(x0) = f' (xо) (x-xо)
или
ỹ = f(x0)+f'(x0)(x-xQ). (2)
Из уравнений (1) и (2) следует, что разность ординат кривой и касательной при одном и том же значении х равна
y-ỹ = f(x)- f(x0) – f’ (xо) (x-xo). Применяя теорему Лагранжа к разности f(x) — f(x0), получим
y- ỹ = f’(с) (х-х0)-f’ (х0) (х-xo)
(где с лежит между х0 и х), или
y- ỹ = [f’ (с)-f’ (х0)](х-х0).
К выражению, стоящему в квадратных скобках, снова применяем теорему Лагранжа; тогда
y- ỹ = f’’ (C1) (с - х0) (х-х0) (3)
(где c1 лежит между х0 и с).
Рассмотрим сначала тот случай, когда x>х0. В этом случае xo <с1<с <х;
так как х — x0>0, с — x0>0 и так как, кроме того, по условию, f " (с1) < 0, то из равенства (3) следует, что
y- ỹ <0.
Рассмотрим теперь случай, когда х < хo. В этом случае x<с< c1 < х0 и х — х0 < 0, с — х0 < 0, а так как по условию f" (c1) <0, то из равенства (3) следует, что у — ỹ < 0.
Таким образом, мы доказали, что любая точка кривой лежит ниже касательной к кривой, каковы бы ни были значения х и х0 на интервале (а, b). А это и значит, что кривая выпукла. Теорема доказана.
Аналогичным образом доказывается теорема для вогнутости
Теорема:
Пусть кривая определяется уравнением y=f(x)
Ecли f’’(a)=0 или f’’(а) не существует и при переходе через значение х=а производная f’’(x) меняет знак, то точка кривой с абциссой х=а есть точка перегиба
Доказательство:
1)Пусть f’’(x)<0 при x<a и f’’(x)>0 при x<a
Тогда при x<a кривая обращена выпуклостью вверх и при x>a выпуклостью вниз. Значит тчк Акривой с абциссой х=а есть точка перегиба.

2)Если f’’(x)>0 при x<b и f’’(x)<0 при x>b, то при x<b кривая обращена выпуклостью вниз, а при x>b выпуклостью вверх. Следовательно, точка В кривой с абциссой x=b есть точка перегиба