2.)Основные правила дифференцирования. Производная обратной функции. Логарифмическое дифференцирование.

Теорема

Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы:

1) (u±v)/=u/±v/,

2) (u·v)/=u/v+v/u,

3) (vu)=v2u/v−v/u.

Доказательство

Из определения производной:

2Теорема

Если функция y=f(x) имеет в точке x_o производную f’(x_o)≠0 то обратная функция x=φ(y) также имеет в соответствующей точке y_o=f(x_o) производную, причем

φ’(y_o)=1/f’(x_o)

Доказательство

Пусть - дифференцируемая функция, .

Пусть - приращение независимой переменной y и Δx - соответствующее приращение обратной функции .

Напишем тождество

(единица делить на частное)

Переходя в этом равенстве к пределу при , которое влечет за собой стремление к нулю (), получим:

, где x'y - производная обратной функции

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.

Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:

Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.

Отсюда видно, что искомая производная равна

3.)Определение дифференцируемой функции. Связь дифференцируемости функции с существованием производной.

ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется дифференцируемой в точке x₀ , если ее приращение в этой точке может быть записано как сумма линейной относительно Dx части и бесконечно малой более высокого порядка чем Dx , т.е.

Df(x₀) = A × Dx + b(Dx) , (1)

где A – число, b(Dx) – б.м. более высокого порядка чем Dx.

Слагаемое A × Dx в выражении (1) (т.е. линейную относительно Dx часть Df(x₀)) называют дифференциалом функции y = f(x) в точке x₀ и обозначают: dy(x₀) , df(x₀) .

ТЕОРЕМА 1 (о связи дифференцируемости с существованием производной).

Функция y = f(x) дифференцируема в точке x₀ Û она имеет в точке x₀ производную. При этом для ее дифференциала в точке x₀ справедливо равенство

dy(x₀) = f ¢(x₀) × Dx . (2)

ДОКАЗАТЕЛЬСТВО

Очевидно, что соответствие (x₀ ; Dx) ® df(x₀) является функцией (двух переменных).

Ее называют дифференциалом функции y = f(x) и обозначают dy , df(x) .

4.)Дифференциал функции: определение, геометрический смысл. Свойства дифференциала. Инвариантность формы записи первого дифференциала. Дифференцирование функций, заданных параметрически.

ОПРЕДЕЛЕНИЕ

Функция y = f(x) называется дифференцируемой в точке x₀ , если ее приращение в этой точке может быть записано как сумма линейной относительно x части и бесконечно малой более высокого порядка чем x , т.е.

f(x₀) = A  x + (x) , (1)

где A – число, (x) – б.м. более высокого порядка чем x.

Слагаемое A  x в выражении (1) (т.е. линейную относительно x часть f(x₀)) называют дифференциалом функции y = f(x) в точке x₀ и обозначают: dy(x₀) , df(x₀) .

Г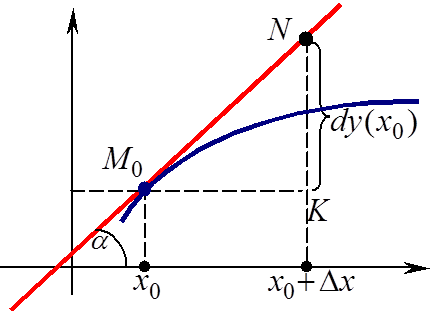ЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА

Рассмотрим график функции y = f(x). Пусть функция y = f(x) дифференцируема в точке x₀. Тогда в x₀ функция f(x) имеет производную f (x₀) . в точке M₀(x₀ ; f(x₀))  касательная к кривой y = f(x). Таким образом, дифференциал функции y = f(x) в точке x₀ равен приращению ординаты точки на

касательной к кривой y = f(x), которое соответствует приращению x.

СВОЙСТВА ДИФФЕРЕНЦИАЛОВ

Из теоремы 1 и правил дифференцирования получаем, что справедливы следующие утверждения

1) Дифференциал константы равна нулю, т.е.

d(C) = 0 , где C – константа.

2) Дифференциал суммы (разности) равна сумме (разности) дифференциалов, т.е. d(u  v) = du  dv .

3) Дифференциал произведения находится по правилу:

d(u  v) = du  v + u  dv .

4) d(C  u) = C  du , где C – константа.

Говорят: «константа выносится за знак дифференциала».

5) Дифференциал дроби находится по правилу:

ИНВАРИАНТНОСТЬ ФОРМЫ ЗАПИСИ ПЕРВОГО ДИФФЕРЕНЦИАЛА

Рассмотрим дифференциал сложной функции y = f((t)) .

Пусть функция x = (t) дифференцируема в точке t, функция y = f(x) дифференцируема в точке x = (t). Тогда  производные x  (t) и f  (x) и сложная функция y = f((t)) имеет производную в точке t , причем y  (t) = [f((t))]  = f  (x)  x  (t) . Следовательно, функция y = f((t)) дифференцируема в точке t и ее дифференциал в этой точке равен

dy(t) = y  (t)  dt ,  dy(t) = f  (x)  x  (t)dt ,  dy = f  (x)  dx . (4)

Сравним формулы (3) и (4):

(3): dy = f  (x)  dx , где x – независимая переменная;

(4): dy = f  (x)  dx , где x = (t) – функция.

Таким образом, формула (3) справедлива вне зависимости от того, является ли x независимым аргументом или функцией.

Поэтому формулу (3) называют инвариантной формой записи дифференциала.

Замечание. Формула dy = f (x)  x  (2) не является инвариантной.

ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

x = x(t), (1)

y = y(t),

где t — вспомогательная переменная, называемая параметром.

Найдем производную считая, что функции (1) имеют произ­водные и что функция х = x(t) имеет обратную t = φ(x). По правилу дифференцирования обратной функции

t’_x = 1/x’_t (2)

Функцию у = f(x), определяемую параметрическими уравнения­ми (1), можно рассматривать как сложную функцию у = y(t), где t = φ(x).

По правилу дифференцирования сложной функции имеем: y'_х = y’_t*t’_х.

С учетом равенства (2) получаем

y'_х = y’_t*(1/x’_t), т.е. y'_х = y’_t/x’_t

Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зави­симости у от х.

Для n-ой производной : y_х⁽ⁿ⁾ = (y_х^(n-1))’_t/x’_t

Замечание. Из теоремы 1 следует, что нахождение производной и дифференциала функции представляет собой по существу одну и ту же задачу. Поэтому операцию нахождения производной называют дифференцированием функции.

ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется дифференцируемой на интервале (a;b) если она дифференцируема (т.е. имеет производную) в каждой точке этого интервала.

ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется дифференцируемой на отрезке [a;b] если она дифференцируема на интервале (a;b) и имеет соответствующие односторонние производные в точках a и b.