
- •1. Простейшая разностная схема для задачи Дирихле
- •1.1 Построение
- •1.2 Аппроксимация
- •1.3 Устойчивость
- •Описания метода установления
- •3. Анализ алгоритмов, реализующих метод установления
- •3.1 Представление решения разностной двумерной задачи теплопроводности в виде конечного ряда Фурье
- •3.2 Анализ явной схемы установления
- •3.3 Анализ схемы переменных направлений
- •3.4 Выбор точности
3.3 Анализ схемы переменных направлений
Займемся
теперь исследованием поведения
погрешности
![]() для
схемы переменных направлений (6) § 2:
для
схемы переменных направлений (6) § 2:
![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решение
![]() задачи
(1) § 2 удовлетворяет уравнениям
задачи
(1) § 2 удовлетворяет уравнениям
![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
![]()
![]()
Вычитая
эти равенства из уравнений (6) § 2
почленно, получим, 1 что погрешность
![]() удовлетворяет разностной краевой
задаче:
удовлетворяет разностной краевой
задаче:
![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]()
![]() 0
0
![]()
![]()
![]()
Имеем следующее решение этой задачи в виде конечного ряда Фурье:
![]()
![]()
![]()
где
![]() –коэффициенты
разложения начальной погрешности
–коэффициенты
разложения начальной погрешности
![]()
![]()
в
конечный ряд Фурье, но числа
![]() уже другие:
уже другие:
![]() =
=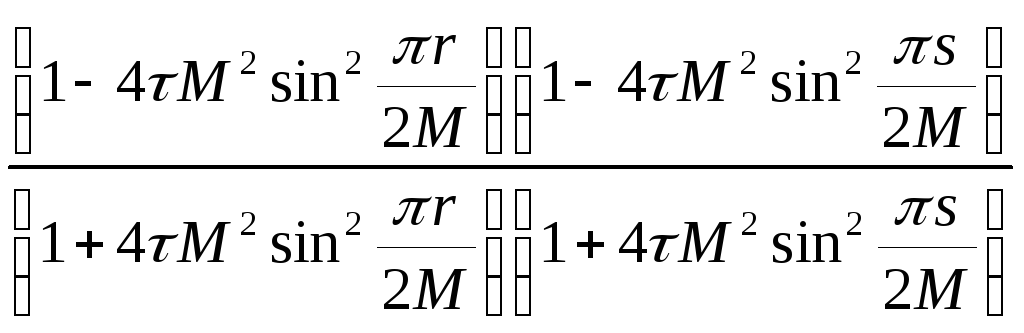 (13) Из предыдущего пункта известно
неравенство:
(13) Из предыдущего пункта известно
неравенство:

Из
выражения (13) для
![]() видно, что при любом
видно, что при любом
![]() выполнено неравенство
выполнено неравенство
![]() <1
и, следовательно, имеет место стремление
<1
и, следовательно, имеет место стремление
![]() к нулю.
к нулю.
Представим
![]() в следующем виде
в следующем виде
![]() ,
где
,
где
![]() =
=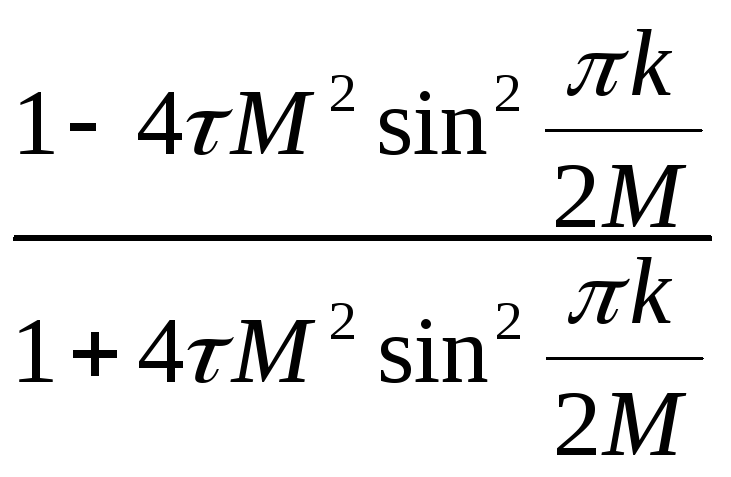 ,
k=1,2,…,
M-1.
,
k=1,2,…,
M-1.
Поэтому
![]() достигается при
достигается при
![]() ,
где
,
где
![]() -
тот номер, при котором величина
-
тот номер, при котором величина
![]() максимальна.
максимальна.
Функция
![]() монотонна
при
монотонна
при
![]() .
Поэтому, если взять
.
Поэтому, если взять
![]() ,
и заметить, что при
,
и заметить, что при
![]() ,
изменяющемся от 1 до
,
изменяющемся от 1 до
![]() ,
,
![]() монотонно
увеличивается, то можно утверждать, что
монотонно
увеличивается, то можно утверждать, что
![]() =
=
лежит
между точками
![]()
![]() и
и
![]()
![]() .
.
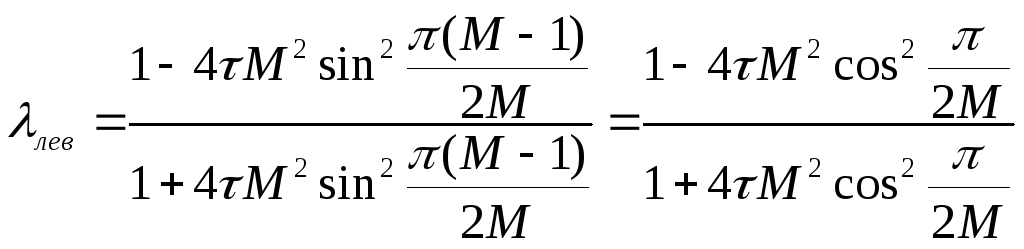 ,
,
так
как
![]()
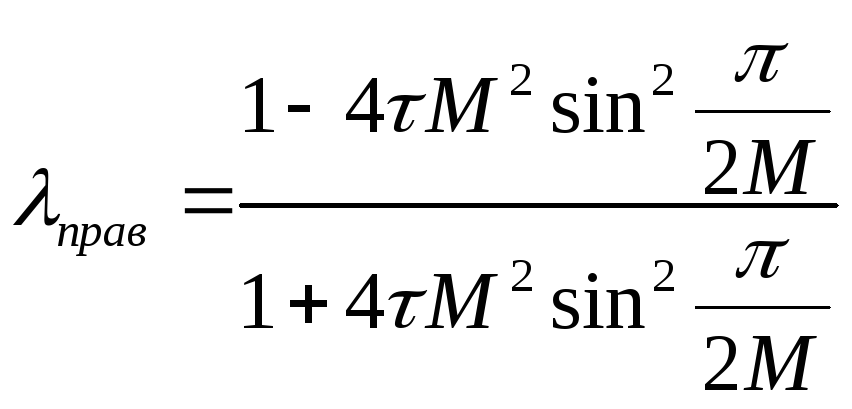
Увеличение
![]() вызывает сдвиг точек
вызывает сдвиг точек
![]() и
и
![]() влево. Поэтому значение
влево. Поэтому значение
![]() будет наименьшим при том
будет наименьшим при том
![]() ,
при котором
,
при котором
![]() .
.

Заменим
![]() на
на
![]() (такая
замена возможна, если считать аргумент
достаточно близким к 0).
(такая
замена возможна, если считать аргумент
достаточно близким к 0).
Тогда
![]() -
оптимальный шаг, при котором происходит
наиболее быстрое убывание погрешности.
-
оптимальный шаг, при котором происходит
наиболее быстрое убывание погрешности.
![]() =
=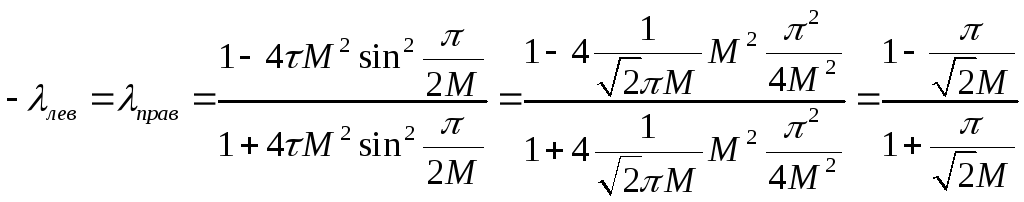

Если
разложить эту функцию в ряд Тейлора по
степеням
![]() ,
то получим:
,
то получим:
![]()
Поэтому
для уменьшения нормы погрешности
![]() в заданное число k
раз по сравнению с первоначальным
значением нормы погрешности
в заданное число k
раз по сравнению с первоначальным
значением нормы погрешности
![]() число шагов р
должно быть найдено из условия
число шагов р
должно быть найдено из условия
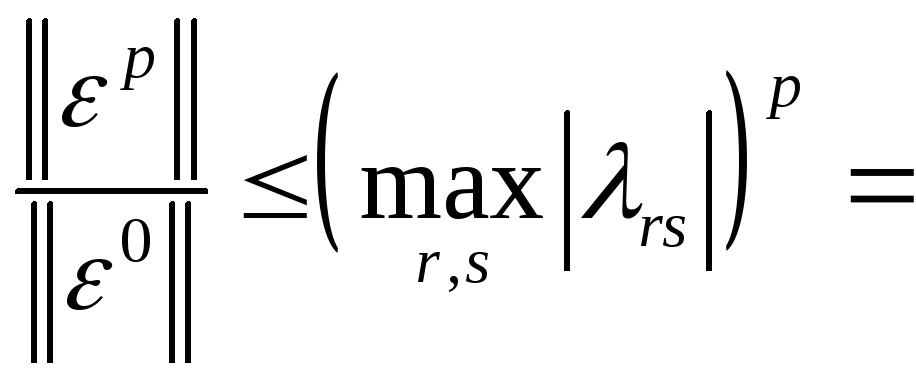
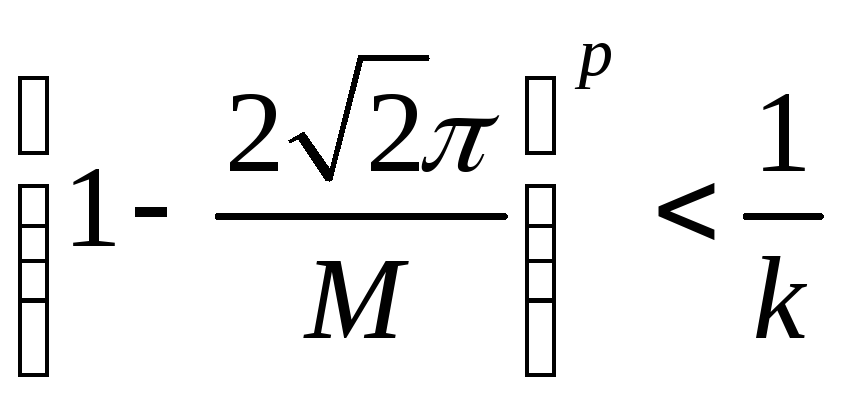
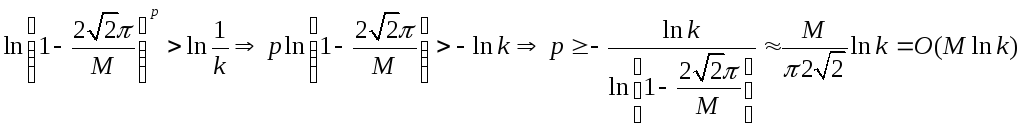
Каждый
переход от
![]() к
к
![]() требует
требует
![]() арифметических
операций. Следовательно, общее число
арифметических операций для уменьшения
ошибки в заданное число k
раз будет
арифметических
операций. Следовательно, общее число
арифметических операций для уменьшения
ошибки в заданное число k
раз будет
![]()
Мы видим, что при больших М второй из рассмотренных нами процессов установления, использующий схему переменных направлений, приводит к уменьшению ошибки в заданное число раз ценой меньших затрат арифметических действий, чем метод установления, основанный на использовании простейшей явной разностной схемы (4): при достаточно больших значениях М (при мелкой сетке) схема переменных направлений оказывается выгоднее.
3.4 Выбор точности
Сделаем
замечание о точности, которой следует
добиваться, решая задачу (1) § 2 методом
установления или другим итерационным
методом, дающим последовательные
приближения
![]() .
Разностная задача (1) § 2 аппроксимирует
задачу (2) § 2 с
порядком
.
Разностная задача (1) § 2 аппроксимирует
задачу (2) § 2 с
порядком
![]() .
Поэтому
точное решение
.
Поэтому
точное решение
![]() задачи (1) § 2 отличается от точного
решения
задачи (1) § 2 отличается от точного
решения
![]() задачи (2) § 2 на величину порядка
задачи (2) § 2 на величину порядка
![]() .
В связи с этим нет смысла вычислять
решение u
задачи (1) § 2 с большей точностью. Если
считать, что нулевое приближение
.
В связи с этим нет смысла вычислять
решение u
задачи (1) § 2 с большей точностью. Если
считать, что нулевое приближение
![]()
![]() задано с погрешностью порядка 1, то число
k
должно быть выбрано порядка М
задано с погрешностью порядка 1, то число
k
должно быть выбрано порядка М![]() .
.
Добиваться
уменьшения первоначальной погрешности
более чем в
![]() раз было бы нецелесообразной затратой
вычислительной работы.
раз было бы нецелесообразной затратой
вычислительной работы.
При
вычислениях на конкретной фиксированной
сетке практически итерируют до тех пор,
пока последовательные приближения
![]() перестанут меняться в пределах
удовлетворяющей нас точности.
перестанут меняться в пределах
удовлетворяющей нас точности.
Заключение
В данной работе были рассмотрен метод установления, а также представлены 2 программы на языке программирования С++, реализующие два алгоритма установления.
В результате было доказано,
что простейшая разностная схема задачи
Дирихле устойчива и аппроксимирует
исходную задачу (1) со вторым порядком
точности относительно h
(![]() ).
).
Также были найдены оптимальные
оценки шага
![]() ,
при которых происходит наиболее быстрое
убывание погрешности.
,
при которых происходит наиболее быстрое
убывание погрешности.
При анализе схем установления
было получено: алгоритм, использующий
схему переменных направлений, эффективнее,
чем алгоритм, использующий явную схему
установления. А именно: объем вычислений
для уменьшения нулевой погрешности в
заданное число раз в первом случае
приблизительно в с![]() М
раз меньше, чем во втором. (
М
раз меньше, чем во втором. (![]() -шаг
сетки, с<<M-константа).
-шаг
сетки, с<<M-константа).
Список использованных источников
-
Тихонов А.Н., Самарский А.А., Уравнения математической физики. М.: «Наука», 1972. 736 с.
-
Годунов С.К., Рябенький В.С. Разностные схемы. М.: «Наука», 1973. 400 с.
-
Березин И.С. и Жидков Н.П. Методы вычислений. т. 1. М.: «Наука», 1965. 633c.
-
Подбельский В.В. и Фомин С.С. Программирование на языке Си. М.: «Финансы и статистика», 2000. 599 с.
Размещено на Allbest.ru
