10.5. Метод Фибоначчи

Рассмотрим все множество последовательных методов для минимизации унимодальных функций. Установлено, что оптимального метода в данном классе не существует. -оптимальным методом (позволяющим сколь угодно близко подойти к минимальной точности) является метод Фибоначчи.

Метод основан на использовании чисел Фибоначчи, которые определяются рекуррентными соотношениями:

Ф ₀ = 1; Ф ₁ = 1; Ф _п = Ф _п-2 + Ф _п-1 ; (п  2) .

Используя коэффициенты   1,618 и   0,618, характеризующие золотое сечение, по индукции можно показать, что числа Фибоначчи представимы также в виде уравнения Люкаса:

Второе слагаемое в уравнении Люкаса быстро стремится к нулю. Уже при сравнительно небольших п (п = 5, 6) его доля составляет менее одного процента и им можно пренебречь. Следовательно, с высокой точностью при п > 5 можно считать:

Ф_n   ⁿ⁺¹ / 2,236.

Число n() необходимых вычислений функции при заданной точности в методе Фибоначчи сокращается за счёт более оптимального выбора последовательности пробных точек. Длина отрезка [a, b] интерпретируется как число Фибоначчи Ф_п+1, умноженное на масштабный коэффициент C: (b-a)=СФ_п+1. Затем данное число разбивается пробными точками на числа Фибоначчи более низкого порядка: СФ_п+1 = СФ_п + СФ_п-1 и т.д., пока не будет получен доверительный отрезок [a_k, b_k] длины b_k - a_k  , где  - заданная точность. Итоговый доверительный отрезок [a_k, b_k] интерпретируется как число Фибоначчи Ф₁=1, умноженное на масштабный коэффициент С=(b-a)/Ф_п+1:

(b_k - a_k )= Ф₁ (b-a)/Ф_п+1 =(b-a)/Ф_п+1 .

Из соотношений Ф_n+1  ⁿ⁺² / 2,236  (b-a)/ = M следует правило приближенного выбора необходимого максимального используемого числа Фибоначчи и величины п: Ф_п+1  (b-a)/ = М, п = ]log _ (2,236 (b-a)/)[ - 2.

Поскольку для программной реализации необходимы точные значения чисел Ф_п, то можно использовать следующие эмпирические формулы, дающие верный результат для п<77 (при этом Ф₇₆  5,52794 10¹⁵ ).

1. Вначале вычисляется величина

Затем рассматриваем два случая: (n<46) и (46n<77).

2. n<46. При четных n, меньших 36: Ф_п := [Р+1], иначе: Ф_п := [Р] .

3. 46  n < 77. Вначале присваиваем Ф_п := [Р] .

При n >70 Ф_п := Ф_п + 70 - n.

При n>74 дополнительно Ф_п := Ф_п +296 - 4n.

4. При n  77 числа Фибоначчи можно определить по основному рекуррентному соотношению, начиная с чисел Ф₇₅ = 3.416.454.622.906.707, Ф₇₆ = 5.527.939.700.884.757.

Метод работает следующим образом.

Предварительные действия (Шаг 0). Рассчитываем масштаб задачи М=(b-а)/, величины п и чисел Фибоначчи Ф _п и Ф _п+1, при которых Ф_п  М  Ф_п+1. Начальный доверительный отрезок принимаем равным исходному: а₀ = а, b₀ = b. Поскольку метод симметричный, то по формулам, содержащим числа Фибоначчи, теоретически достаточно рассчитать только положение на отрезке [а₀, b₀] первой точки. Вычисление производим по формуле

х₁ = а + (b - a) Ф _п-1 / Ф _п+1 = а + С Ф _п-1.

В полученной точке вычисляем значение функции F(х₁), переходим к Шагу 1.

Шаги i= 1  (n-1). К их началу известны :

а) доверительный отрезок [a_i-1, b_i-1] длины _i = b_i-1 - a_i-1 = С Ф _п+2–i ,

б) пробная точка х, в которой уже найдено значение функции F(х ), отстоящая от ближнего края отрезка [a_i-1, b_i-1] на расстоянии: _i Ф _{п – i}/ Ф _{п+2– i} .

Расчет новой пробной точки, функции в ней и упорядочение пробных точек и сокращение доверительного отрезка выполняем, как и в методе золотого сечения:

1. Расчет положения новой пробной точки: х = (b_i-1 + а_i-1) - х, расчет значения функции F(x).

2. Упорядочение пробных точек х, х и значений функции в них:

если (х < х), то { х₁ = х; F(x₁)=F(x); х₂ = х ; F(x₂)=F(x) };

иначе { х₁ = х ; F(x₁)=F(x) ; х₂ = х ; F(x₂)=F(x) }.

3. Сокращение доверительного отрезка:

а) при F(x₁)  F(x₂) принимаем: a₁ = х₁ , х₁ = х₂ , b₁ = b₀ ,

б) при F(x₁) < F(x₂) принимаем: a₁ = а₀ , х₂ = х₁ , b₁ = х₂ .

Характеристики произвольного i-го шага:

а) длина отбрасываемой части отрезка:  _i = _i-1 Ф _{п –i} / Ф _п–i+2 = С Ф _{п – i+1} ,

б) длина оставшегося доверительного отрезка [a _i ,b _i]: _i = _i-1 - _i = С Ф _{п– i+1} .

Шаг n (заключительный). К началу известен :

а) доверительный отрезок [a_n-1, b_n-1] длины _n-1 = b_n-1 - a_n-1 = С Ф ₂ ,

б) пробная точка х, в которой уже найдено значение функции F(х), отстоящая от ближнего края отрезка [a_n-1, b_n-1] на расстоянии: _n-1 Ф ₁/ Ф ₂ =0, 5 _n-1.

Особенностью заключительного шага является то, что известная пробная точка х теоретически лежит точно в средней точке доверительного отрезка [a_n-1, b_n-1]. В силу этого вторую пробную точку нельзя рассчитывать как симметричную х относительно центра [a_n-1, b_n-1], поскольку она совпадёт с х.

Поэтому на последнем Шаге п принимаем:

x₁ := x ; F(x₁):= F(x); x₂ := x₁ + ;

где  - некоторое малое число, можно принять =0,1.

После вычисления F(х₂) производим по обычной схеме анализ F(х₁), F(х₂) и последнее сокращение доверительного отрезка.

Итоговая длина _п доверительного отрезка равна СФ₁ +  либо С Ф ₁ .

Если число Ф_п+1 близко к М, то из-за сдвига точки x₂ на  длина _n может незначительно превысить гарантированную точность  .

Скорость сходимости и точность метода. Учитывая, что на первом шаге функция рассчитывается дважды, получим величину n() для метода Фибоначчи:

n() = ]log_ (2,236(b-a)/)[-1.

Из этого же уравнения находим зависимость (n) точности от общего числа вычислений функции:

(n)  2,236(b-a)/ ^п+1=2,236 (b - a) ⁽ⁿ⁺¹⁾.

Разделив точность метода золотого сечения  (п) = (b - a) ^(n-1) на эту величину, получим значение 1/( 2,236 ² )  1,17. Таким образом, при n   метод золотого сечения в среднем хуже метода Фибоначчи (при заданном числе вычислений больше длина получаемого доверительного отрезка) приблизительно на 17%.

Замечание. При достаточно больших n, как следует из приближённого уравнения Люкаса, отношение Ф _п / Ф _п+1 стремится к коэффициенту  = 1/. Следовательно, первая пробная точка метода Фибоначчи х₁ = а + (b - a) Ф _п-1 / Ф_п+1 стремится к первой пробной точке х₁ метода золотого сечения.

Метод Фибоначчи является самым быстрым из регулярных последовательных методов, применяемых для минимизации однопараметрических унимодальных функций на отрезке.

Пример 1. Найти минимум функции F(х) = х² –2х на исходном доверительном отрезке [0,2; 2] по методу Фибоначчи при заданной точности  =0,5.

Решение.

Шаг 0. Предварительные действия. Масштаб задачи М = (b-a)/=3,6. Из соотношений Ф₃ =3 < 3,6 < Ф₄ =5 следует: n=3, Ф_п+1 = 5, Ф_п = 3.

Доверительный отрезок: а₀ = а =0,2; b₀ = b=2.

Шаг 1. Пробные точки: х₂ = а₀ + (b₀ - a₀) Ф _п / Ф _п+1 = 1,28; х₁ = а₀ + b₀ - х₂ = 0,92.

Значения функции: F(x₁)=-0,9936; F(x₂)=-0,9216. F(x₁)< F(x₂), поэтому отбрасываем часть отрезка [x₂;b₀]. Получаем новый отрезок [а₁;b₁]= [0,2;1,28].

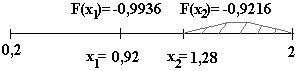
b₁-а₁ = 1,08 >  = 0,5; продолжаем поиск.

Шаг 2. Границы доверительного отрезка а₁=0,2; b₁=1,28. Известно значение F(x) = -0,9936 при х=0,92.

Новая пробная точка: х = а₁ + b₁ - х = 0,56. Значение функции в ней: F(x)= -0,8064.

Т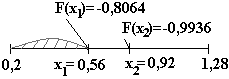ак как х < х, то принимаем: х₁ = х ; F(x₁)=F(x); х₂ = х; F(x₂)=F(x). Поскольку F(x₁)>F(x₂), то отбрасываем часть доверительного отрезка, равную [a₁;x₁].

Получаем новый доверительный отрезок [а₂;b₂]= [0,56;1,28]. Так как b₂-а₂=0,72 > ; то продолжаем поиск.

Шаг 3 (заключительный).Границы доверительного интервала а₂=0,56; b₂=1,28. Известно значение F(x) = -0,9936 при х=0,92.

Новую пробную точку строим сдвигом известной: х = 0,92+0,01=0,93. Значение функции в ней: F(x) = -0,9951.

Поскольку х>х, то полагаем х₁=х; F(x₁)=F(x); х₂=х ; F(x₂)=F(x).

Так как F(x₁)>F(x₂), то отбрасываем часть доверительного отрезка [a;x₁]. Получаем итоговый отрезок [а₃;b₃]= [0,92;1,28]. b₃-а₃=0,36 < ; поиск завершаем.

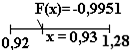
Ответ. Выполнено 3 шага при 4 пробных точках. Найден доверительный интервал [а₃, b₃] = [0,92; 1,28] длины 0,36.

По сравнению с методом золотого сечения число вычислений функции осталось прежним, но сократилась длина итогового доверительного интервала с 0,4248 до 0,36.

Несмотря на то, что метод Фибоначчи является самым быстрым из регулярных последовательных методов, применяемых для минимизации однопараметрических унимодальных функций на отрезке, он не намного лучше метода золотого сечения при том, что значительно сложнее в реализации.

Вопросы для проверки знаний.

1. Какая числовая последовательность называется числами Фибоначчи ?

2. В каком виде числа Фибоначчи могут быть явно представлены в а) точной и б) приближенной формах ?

3. Как по заданному масштабу задачи определить число итераций п, необходимое для ее решения по методу Фибоначчи ? Какие дополнительные данные помимо п требуются для начала итераций ?

4. Чем отличается первый шаг от последующих в методе Фибоначчи ?

5. Какая особенность заключается в выполнении последнего шага в методе Фибоначчи ?

6. К какому методу стремятся при числе итераций n   положения первых пробных точек в методе Фибоначчи ?

Практические задания.

1. Рассчитать величину п и чисел Фибоначчи Ф_п, Ф_п+1, удовлетворяющих условию Ф_п  М  Ф_п+1, в следующих случаях:

а) а=2, b=12,  = 0,1;

б) а= -10, b=10,  = 0,2.

2. Решить по методу Фибоначчи задачи 1)-13) из п.10.2.