
- •О конечных пределах
- •Эквивалентных бесконечно малых величин
- •Точка разрыва функции
- •Производная и дифференциал Вычисление производных
- •Дифференцирование сложной функции
- •И дифференциала функции
- •Применение правила Лопиталя к нахождению предела функции
- •Раскрытие неопределенностей типа и
- •Раскрытие неопределенностей типа и
- •Раскрытие неопределенностей типа
- •Применение производной к исследованию функции. Построение графиков функций Промежутки монотонности и точки экстремума функции
- •Выпуклость и вогнутость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Общий план исследования функции
Производная и дифференциал Вычисление производных
Основные правила дифференцирования:
Если функция и(х) и v(x) дифференцируемы в точке х, то в этой точке:
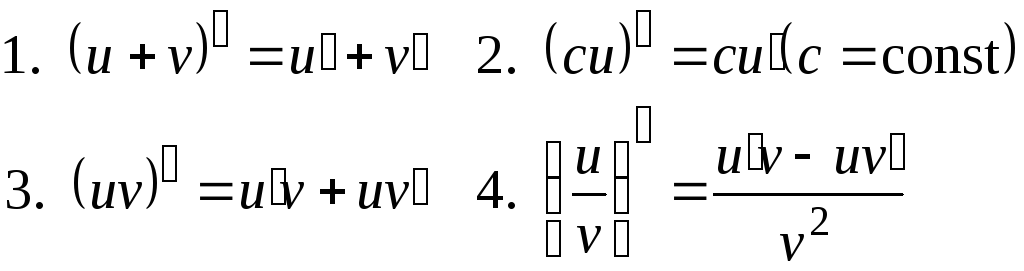
Таблица производных:
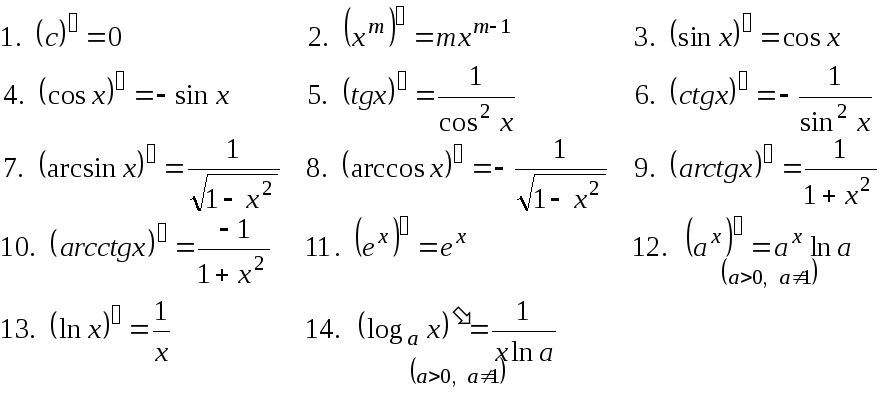 ПРИМЕР
21. Найти
производную функции
ПРИМЕР
21. Найти
производную функции
![]()
РЕШЕНИЕ: Используем первое и второе правила дифференцирования
![]()

Далее используем формулу для нахождения производной степенной функции (табличная формула N 2):
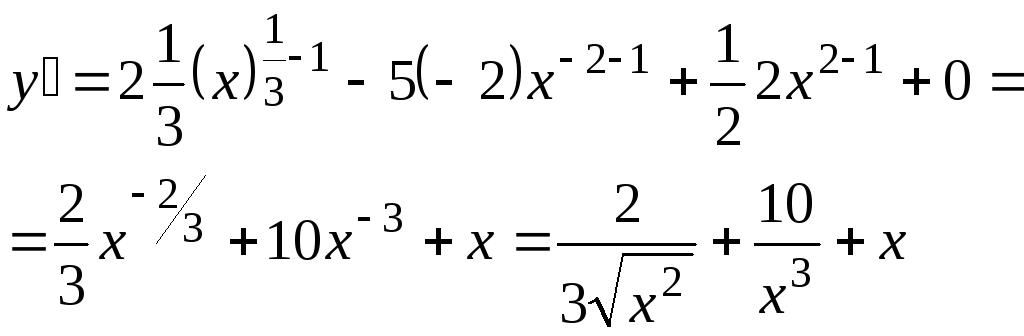
ПРИМЕР
22. Найти
производную функции
![]()
РЕШЕНИЕ: Используем правило дифференцирования произведения и табличные формулы N 4 и N 11:
![]()
ПРИМЕР
23. Найти
производную функции
![]()
РЕШЕНИЕ: Используем правило дифференцирования частного и табличные формулы N 9 и N 13:
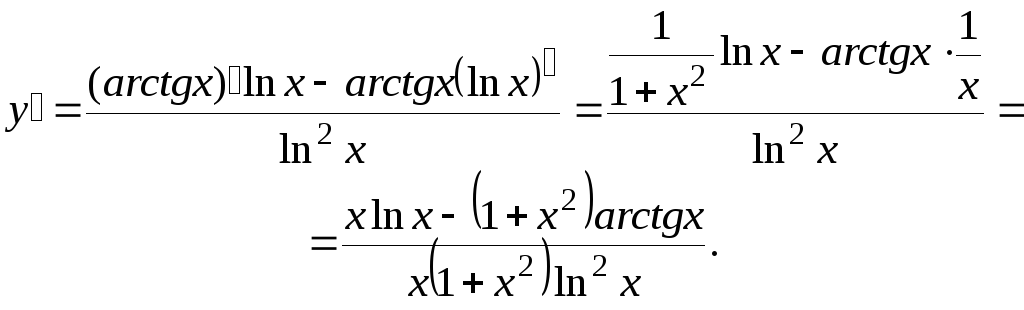
Дифференцирование сложной функции
Производная сложной функции у = f(u(x)) вычисляется по формуле
![]()
То есть, чтобы найти производную сложной функции, нужно сначала продифференцировать "внешнюю" функцию по промежуточному аргументу и так, как если бы аргумент и был независимой переменной, после чего умножить полученный результат на производную от функции и по переменной х.
Это правило распространяется на сложную функцию, состоящую из любого конечного числа дифференцируемых функций.
ПРИМЕР
24. Найти
производную функции
![]()
РЕШЕНИЕ:
Данная
функция - сложная, промежуточный аргумент
![]() .
Согласно приведенному правилу имеем
.
Согласно приведенному правилу имеем
![]()
ПРИМЕР
25.
Найти производную функции
![]()
РЕШЕНИЕ:
Данная
сложная функция составлена из трех
функций
![]() где
где
![]() Применяем правило
дифференцирования сложной функции
(начиная дифференцировать
с "внешней" функции f
):
Применяем правило
дифференцирования сложной функции
(начиная дифференцировать
с "внешней" функции f
):
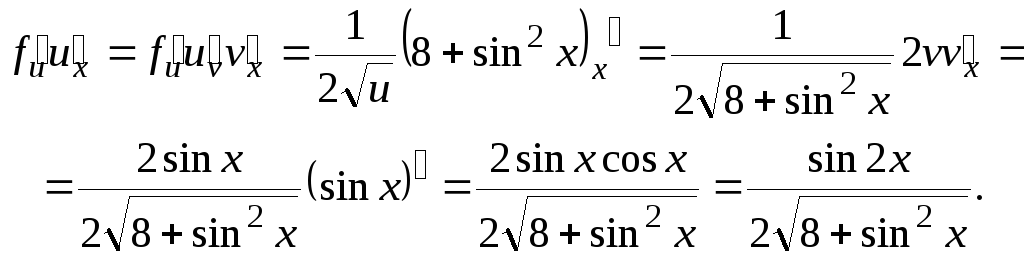
Геометрический смысл производной
И дифференциала функции
Пусть
в декартовой прямоугольной системе
координат задана кривая,
являющаяся графиком функции
![]() и
на ней точка
и
на ней точка
![]() Производная
Производная
![]() функции
функции
![]() геометрически
представляет собой
угловой
коэффициент касательной к графику
функции в точке с абсциссой
геометрически
представляет собой
угловой
коэффициент касательной к графику
функции в точке с абсциссой
![]() ,
т.е.
,
т.е.
![]() (см.
рис.12). Тогда уравнение
касательной
к кривой
(см.
рис.12). Тогда уравнение
касательной
к кривой
![]() в
точке
в
точке
![]() имеет
вид:
имеет
вид:
![]()
Дифференциал
функции f(x)
в
точке
![]() находится по формуле
находится по формуле
![]() ,
т.е. равен произведению производной
функции в
заданной точке на дифференциал(приращение)
независимой переменной. Геометрически
дифференциал функции
,
т.е. равен произведению производной
функции в
заданной точке на дифференциал(приращение)
независимой переменной. Геометрически
дифференциал функции
![]() в точке
в точке
![]() представляет
собой приращение
ординаты касательной к
графику функции в
точке
представляет
собой приращение
ординаты касательной к
графику функции в
точке
![]() и при
и при
![]() являются
эквивалентными бесконечно малыми.
Поэтому справедливо приближенное
равенство
являются
эквивалентными бесконечно малыми.
Поэтому справедливо приближенное
равенство
![]() ~
dy,
позволяющее
приближенно заменять приращение функции
дифференциалом.
~
dy,
позволяющее
приближенно заменять приращение функции
дифференциалом.
ПРИМЕР
26. Найти
координаты точки пересечения с осью Оу
касательной
к кривой
![]() ,
где
,
где
![]() ,
проведенной к ней в точке
,
проведенной к ней в точке
![]()
РЕШЕНИЕ:
Уравнение
касательной к кривой
![]() в точке
в точке
![]() имеет
вид
имеет
вид
![]() .
Найдем
сначала производную
.
Найдем
сначала производную
![]() :
:
![]()
Вычислим
![]() тогда уравнение касательной к заданной
кривой в точке Мо(-1,4)
запишется в виде:
тогда уравнение касательной к заданной
кривой в точке Мо(-1,4)
запишется в виде:
![]()
Теперь находим координаты точки пересечения полученной прямой с осью Оу.
Для всех точек, лежащих на оси Оу, х = 0. Подставим в уравнение касательной х = 0, получим у = 8. Значит, касательная у = 4х + 8 пересекает ось Оу в точке(0,8).
Применение правила Лопиталя к нахождению предела функции
При
отыскании предела
![]() подстановка
предельного значения
подстановка
предельного значения
![]() в
ряде случаев приводит к неопределенным
выражениям типа:
в
ряде случаев приводит к неопределенным
выражениям типа:
![]() .
Тогда
вычисление заданного
предела называют раскрытием неопределенности
соответствующего
типа. Обычно при этом используют правило
Лопиталя.
.
Тогда
вычисление заданного
предела называют раскрытием неопределенности
соответствующего
типа. Обычно при этом используют правило
Лопиталя.
