Эквивалентных бесконечно малых величин

Функции бесконечно малые при называются эквивалентными, если . Эквивалентность бесконечно малых обозначается так: ~ при . При раскрытии неопределенностей можно пользоваться правилом: предел отношения двух бесконечно малых не изменится, если эти бесконечно малые под знаком предела заменить им эквивалентными. Если при - бесконечно малая, то есть то

~ ; ~ ; ~ ;

~ ; ~ ; ~ ;

~ ; ~ ; ~ .

ПРИМЕР 17. Найти

РЕШЕНИЕ: Так как при то имеем неопределенность Заменим исходные бесконечно малые эквивалентными

~ ; ~ ; ~ ; ~

Непрерывность функции в точке и на промежутке.

Точка разрыва функции

Если функция у = f(х) определена в некоторой окрестности конечной точки а, то точка а называется точкой разрыва функции в двух случаях:

1. в точке х = а функция f(х) не определена;

2. в точке х = а функция f(х) определена, но не выполняется хотя бы одно из равенств:

(3)

где - левосторонний и правосторонний пределы функции в точке а.

Если при этом конечны, то точка х = а называется точкой разрыва первого рода (или точкой конечного разрыва) .Причем, если ,то разрыв называется устранимым.

Если хотя бы один из пределов в равенстве (3) не существует или бесконечный, то точка a называется точкой разрыва второго рода (точкой бесконечного разрыва, если хотя бы один из соответствующих пределов - бесконечный).

Все элементарные функции непрерывны в каждой точке области определения.

ПРИМЕР 18. Найти точки разрыва функции у = f(x), определить тип разрыва. Для точек разрыва первого рода вычислить скачок функции. Построить график.

РЕШЕНИЕ: Внутри каждого из промежутков (;0), (0; 1) и (1;) функция f(x) совпадает с соответствующей элементарной функцией. Следовательно, внутри каждого из этих промежутков функция f(x) будет непрерывной, и разрывы могут быть только на концах этих промежутков, то есть в точках x=0 и x=1.

Найдем односторонние пределы в этих точках:

1. Для точки х = 0 имеем:

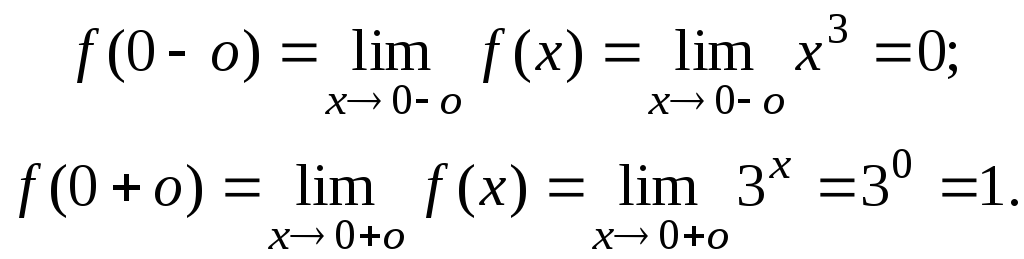
Оба односторонних предела конечны, но не равны между собой, значит, точка х = 0 есть точка разрыва I рода. В точке х = 0 функция f(x) имеет скачок

2. Рассмотрим точку х = 1.

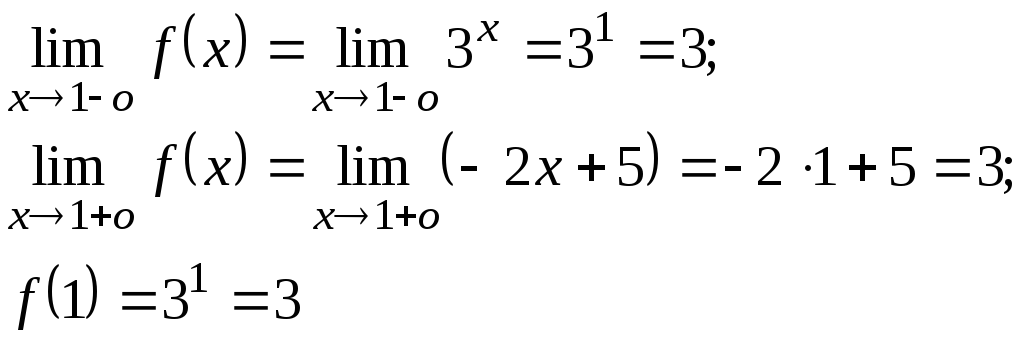
Односторонние пределы равны и совпадают со значением функции в рассматриваемой точке, значит, в этой точке функция f(x) непрерывна. График функции изображен на рис.9.

ПРИМЕР 19. Найти точки разрыва функции , установить тип разрыва, для точек разрыва первого рода вычислить скачок функции, построить график в окрестности точек разрыва.

РЕШЕНИЕ: Преобразуем дробь:

Функция не определена в точках х = -1 и х = 3 и, следовательно, имеет в этих точках разрывы. Найдем соответствующие односторонние пределы:

1. Для точки х = -1 при 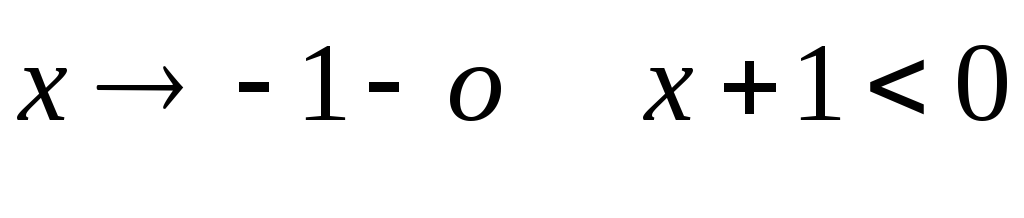и, значит, Следовательно,

Аналогично вычислим

Так как оба предела конечны, то точка х = - 1 - точка разрыва первого рода. Поскольку пределы не равны, то это - конечный разрыв I рода. - скачок функции. В окрестности точки x = 3 х + 1>0, поэтому |х + 1| = х + 1 и, значит

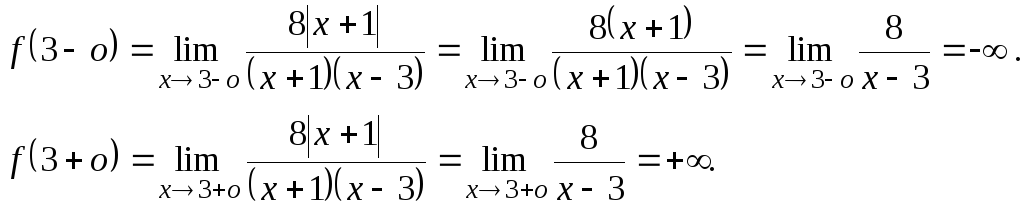
Таким образом, точка х = 3 - точка бесконечного разрыва второго рода. График функции представлен на рис.10.

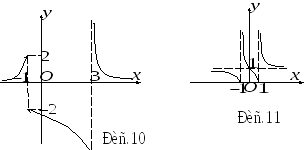ПРИМЕР 20. Найти точки разрыва функции , определить тип разрыва, начертить эскиз графика функции в окрестности точек разрыва.

РЕШЕНИЕ: Данная элементарная функция не определена в точках х = - 1 и х = 1 и, следовательно, имеет в этих точках разрывы. Найдем односторонние пределы, учитывая, что

1. Рассмотрим точку х = - 1.

Так как при то

При

Следовательно,

Таким образом, точка х = - 1 - точка бесконечного разрыва второго рода.

2. Рассмотрим точку x = 1. Аналогично предыдущему получаем

то есть в точке x = 1 функция имеет бесконечный разрыв второго рода.

2. Рассмотрим поведение функции при

Следовательно, у = 1 - асимптота функции. Эскиз графика функции изображен на рис.11.